A Zeroth-Order Block Coordinate Descent Algorithm for Huge-Scale Black-Box Optimization

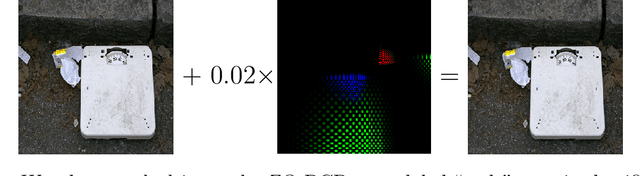
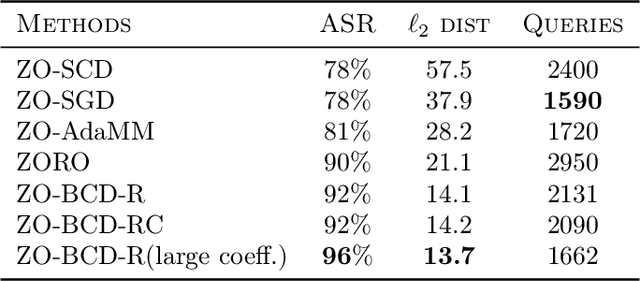
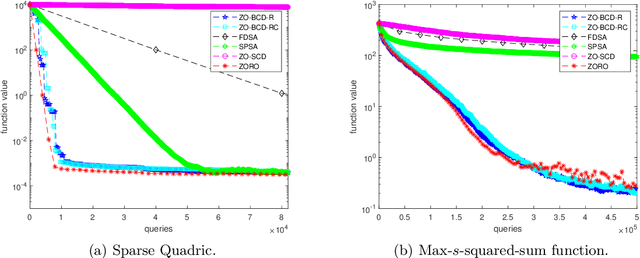
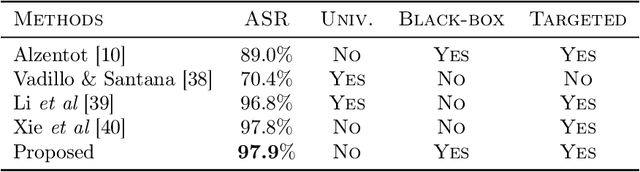
We consider the zeroth-order optimization problem in the huge-scale setting, where the dimension of the problem is so large that performing even basic vector operations on the decision variables is infeasible. In this paper, we propose a novel algorithm, coined ZO-BCD, that exhibits favorable overall query complexity and has a much smaller per-iteration computational complexity. In addition, we discuss how the memory footprint of ZO-BCD can be reduced even further by the clever use of circulant measurement matrices. As an application of our new method, we propose the idea of crafting adversarial attacks on neural network based classifiers in a wavelet domain, which can result in problem dimensions of over 1.7 million. In particular, we show that crafting adversarial examples to audio classifiers in a wavelet domain can achieve the state-of-the-art attack success rate of 97.9%.

CADA: Communication-Adaptive Distributed Adam

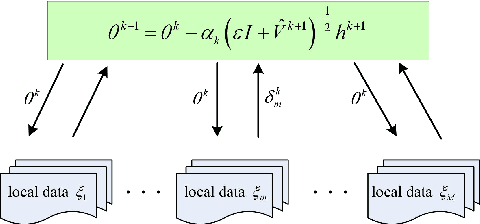
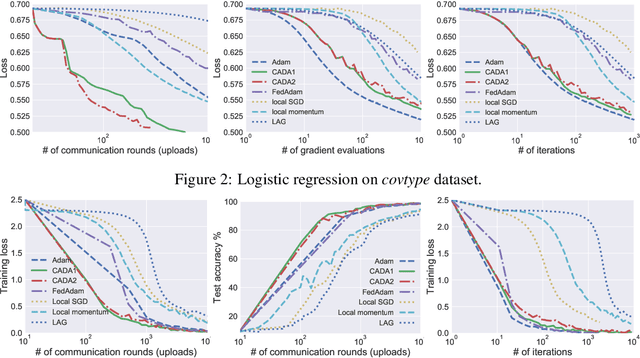
Stochastic gradient descent (SGD) has taken the stage as the primary workhorse for large-scale machine learning. It is often used with its adaptive variants such as AdaGrad, Adam, and AMSGrad. This paper proposes an adaptive stochastic gradient descent method for distributed machine learning, which can be viewed as the communication-adaptive counterpart of the celebrated Adam method - justifying its name CADA. The key components of CADA are a set of new rules tailored for adaptive stochastic gradients that can be implemented to save communication upload. The new algorithms adaptively reuse the stale Adam gradients, thus saving communication, and still have convergence rates comparable to original Adam. In numerical experiments, CADA achieves impressive empirical performance in terms of total communication round reduction.

Hybrid Federated Learning: Algorithms and Implementation

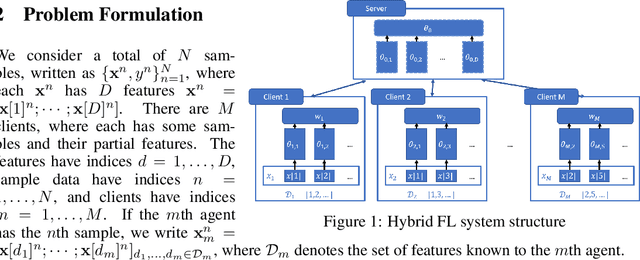
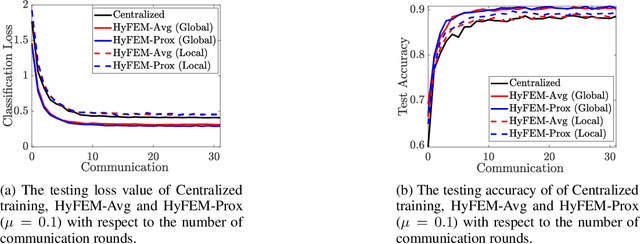
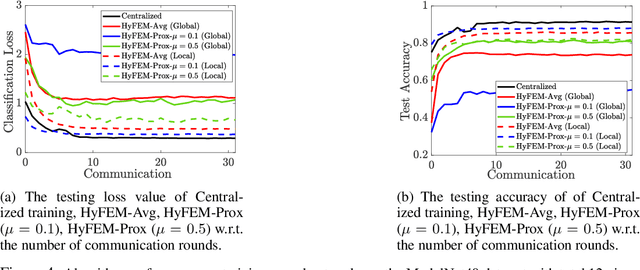
Federated learning (FL) is a recently proposed distributed machine learning paradigm dealing with distributed and private data sets. Based on the data partition pattern, FL is often categorized into horizontal, vertical, and hybrid settings. Despite the fact that many works have been developed for the first two approaches, the hybrid FL setting (which deals with partially overlapped feature space and sample space) remains less explored, though this setting is extremely important in practice. In this paper, we first set up a new model-matching-based problem formulation for hybrid FL, then propose an efficient algorithm that can collaboratively train the global and local models to deal with full and partial featured data. We conduct numerical experiments on the multi-view ModelNet40 data set to validate the performance of the proposed algorithm. To the best of our knowledge, this is the first formulation and algorithm developed for the hybrid FL.

Attentional Biased Stochastic Gradient for Imbalanced Classification

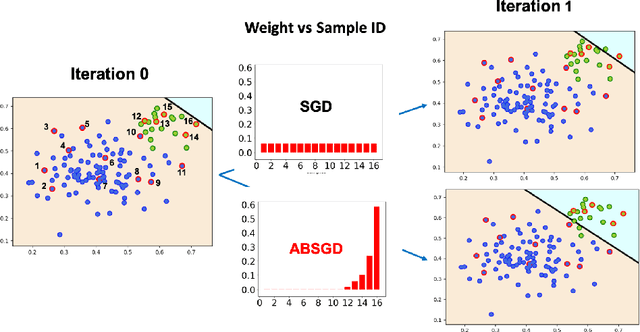
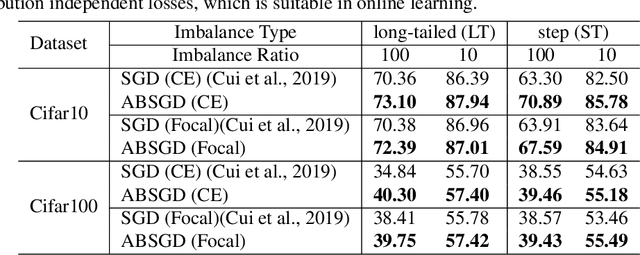
In this paper~\footnote{The original title is "Momentum SGD with Robust Weighting For Imbalanced Classification"}, we present a simple yet effective method (ABSGD) for addressing the data imbalance issue in deep learning. Our method is a simple modification to momentum SGD where we leverage an attentional mechanism to assign an individual importance weight to each gradient in the mini-batch. Unlike existing individual weighting methods that learn the individual weights by meta-learning on a separate balanced validation data, our weighting scheme is self-adaptive and is grounded in distributionally robust optimization. The weight of a sampled data is systematically proportional to exponential of a scaled loss value of the data, where the scaling factor is interpreted as the regularization parameter in the framework of information-regularized distributionally robust optimization. We employ a step damping strategy for the scaling factor to balance between the learning of feature extraction layers and the learning of the classifier layer. Compared with exiting meta-learning methods that require three backward propagations for computing mini-batch stochastic gradients at three different points at each iteration, our method is more efficient with only one backward propagation at each iteration as in standard deep learning methods. Compared with existing class-level weighting schemes, our method can be applied to online learning without any knowledge of class prior, while enjoying further performance boost in offline learning combined with existing class-level weighting schemes. Our empirical studies on several benchmark datasets also demonstrate the effectiveness of our proposed method

SCOBO: Sparsity-Aware Comparison Oracle Based Optimization

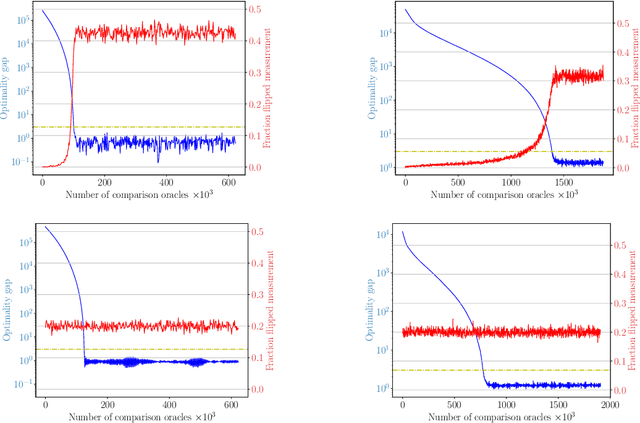
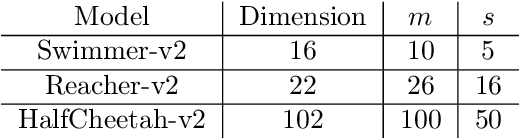
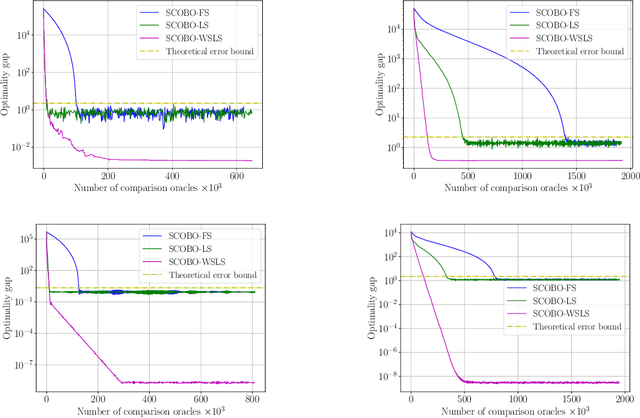
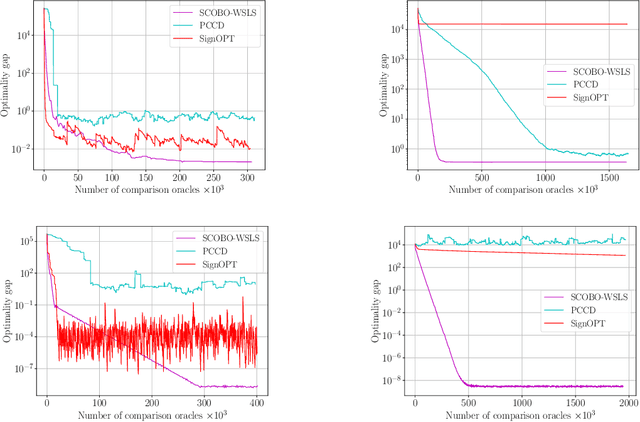
We study derivative-free optimization for convex functions where we further assume that function evaluations are unavailable. Instead, one only has access to a comparison oracle, which, given two points $x$ and $y$, and returns a single bit of information indicating which point has larger function value, $f(x)$ or $f(y)$, with some probability of being incorrect. This probability may be constant or it may depend on $|f(x)-f(y)|$. Previous algorithms for this problem have been hampered by a query complexity which is polynomially dependent on the problem dimension, $d$. We propose a novel algorithm that breaks this dependence: it has query complexity only logarithmically dependent on $d$ if the function in addition has low dimensional structure that can be exploited. Numerical experiments on synthetic data and the MuJoCo dataset show that our algorithm outperforms state-of-the-art methods for comparison based optimization, and is even competitive with other derivative-free algorithms that require explicit function evaluations.

Solving Stochastic Compositional Optimization is Nearly as Easy as Solving Stochastic Optimization

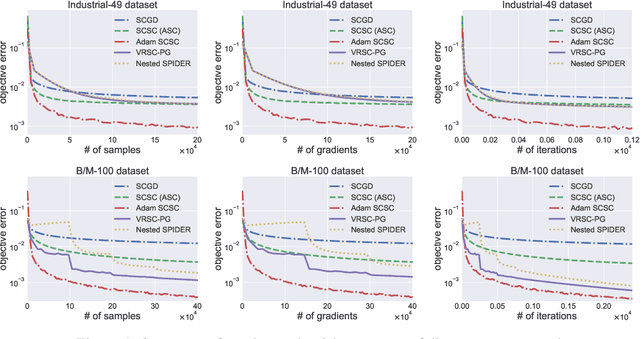
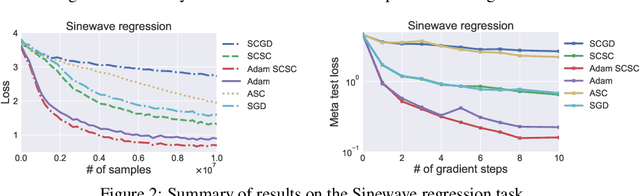
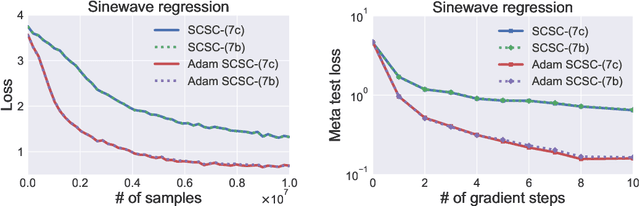
Stochastic compositional optimization generalizes classic (non-compositional) stochastic optimization to the minimization of compositions of functions. Each composition may introduce an additional expectation. The series of expectations may be nested. Stochastic compositional optimization is gaining popularity in applications such as reinforcement learning and meta learning. This paper presents a new Stochastically Corrected Stochastic Compositional gradient method (SCSC). SCSC runs in a single-time scale with a single loop, uses a fixed batch size, and guarantees to converge at the same rate as the stochastic gradient descent (SGD) method for non-compositional stochastic optimization. This is achieved by making a careful improvement to a popular stochastic compositional gradient method. It is easy to apply SGD-improvement techniques to accelerate SCSC. This helps SCSC achieve state-of-the-art performance for stochastic compositional optimization. In particular, we apply Adam to SCSC, and the exhibited rate of convergence matches that of the original Adam on non-compositional stochastic optimization. We test SCSC using the portfolio management and model-agnostic meta-learning tasks.

Projecting to Manifolds via Unsupervised Learning

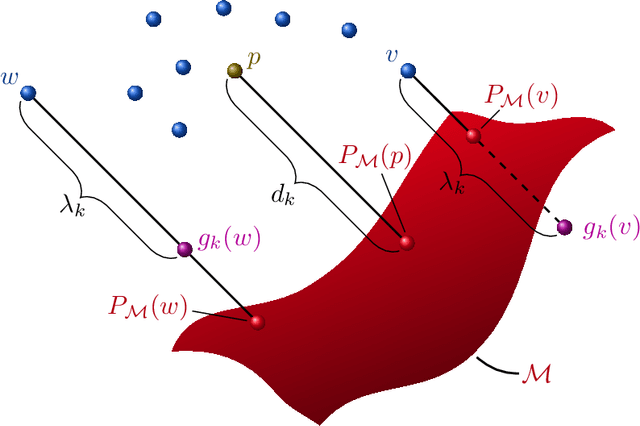
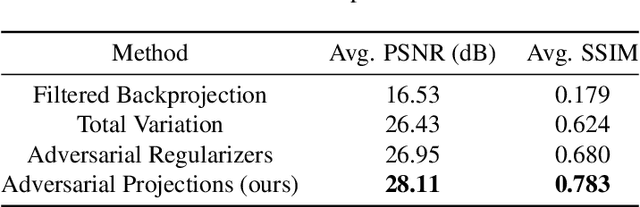
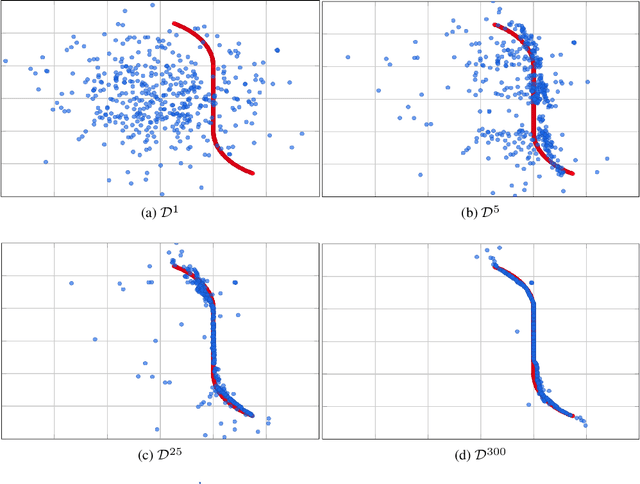
We present a new framework, called adversarial projections, for solving inverse problems by learning to project onto manifolds. Our goal is to recover a signal from a collection of noisy measurements. Traditional methods for this task often minimize the addition of a regularization term and an expression that measures compliance with measurements (e.g., least squares). However, it has been shown that convex regularization can introduce bias, preventing recovery of the true signal. Our approach avoids this issue by iteratively projecting signals toward the (possibly nonlinear) manifold of true signals. This is accomplished by first solving a sequence of unsupervised learning problems. The solution to each learning problem provides a collection of parameters that enables access to an iteration-dependent step size and access to the direction to project each signal toward the closest true signal. Given a signal estimate (e.g., recovered from a pseudo-inverse), we prove our method generates a sequence that converges in mean square to the projection onto this manifold. Several numerical illustrations are provided.

VAFL: a Method of Vertical Asynchronous Federated Learning

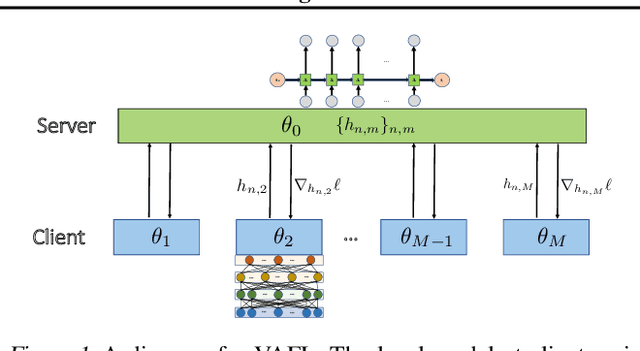
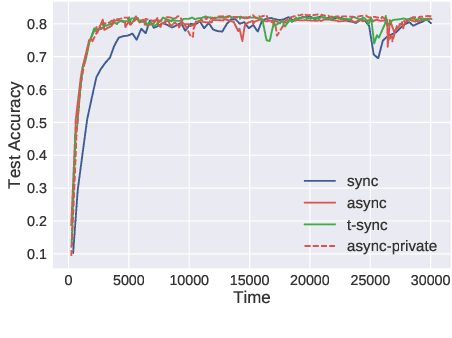
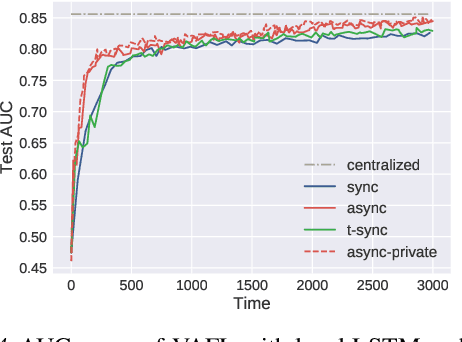
Horizontal Federated learning (FL) handles multi-client data that share the same set of features, and vertical FL trains a better predictor that combine all the features from different clients. This paper targets solving vertical FL in an asynchronous fashion, and develops a simple FL method. The new method allows each client to run stochastic gradient algorithms without coordination with other clients, so it is suitable for intermittent connectivity of clients. This method further uses a new technique of perturbed local embedding to ensure data privacy and improve communication efficiency. Theoretically, we present the convergence rate and privacy level of our method for strongly convex, nonconvex and even nonsmooth objectives separately. Empirically, we apply our method to FL on various image and healthcare datasets. The results compare favorably to centralized and synchronous FL methods.

FedPD: A Federated Learning Framework with Optimal Rates and Adaptivity to Non-IID Data

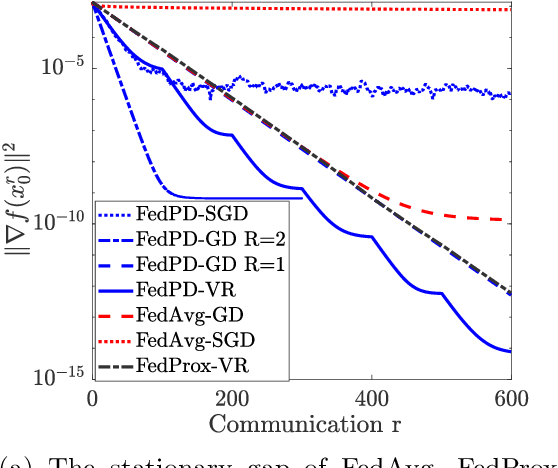
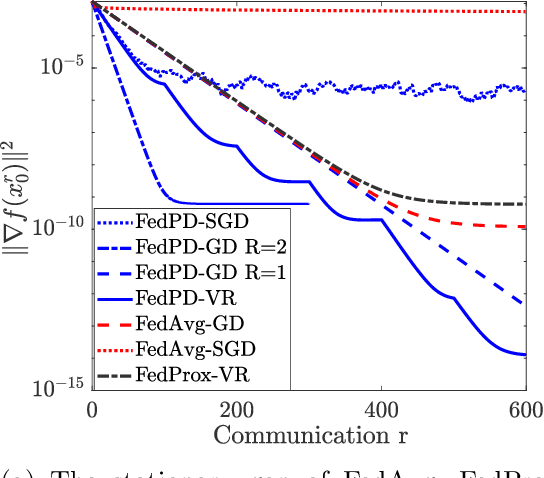
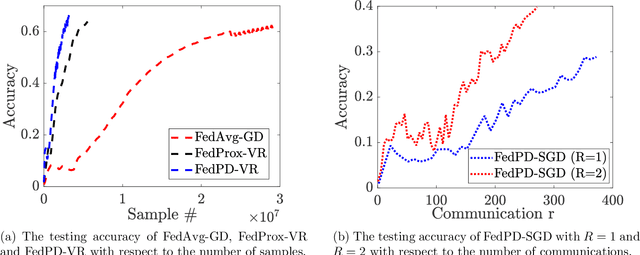
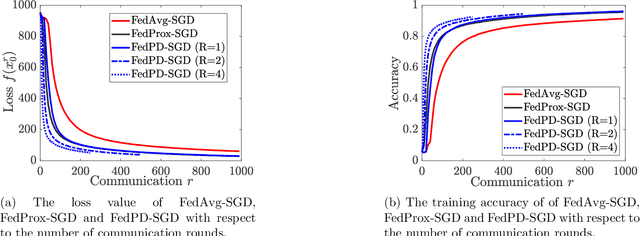
Federated Learning (FL) has become a popular paradigm for learning from distributed data. To effectively utilize data at different devices without moving them to the cloud, algorithms such as the Federated Averaging (FedAvg) have adopted a "computation then aggregation" (CTA) model, in which multiple local updates are performed using local data, before sending the local models to the cloud for aggregation. However, these schemes typically require strong assumptions, such as the local data are identically independent distributed (i.i.d), or the size of the local gradients are bounded. In this paper, we first explicitly characterize the behavior of the FedAvg algorithm, and show that without strong and unrealistic assumptions on the problem structure, the algorithm can behave erratically for non-convex problems (e.g., diverge to infinity). Aiming at designing FL algorithms that are provably fast and require as few assumptions as possible, we propose a new algorithm design strategy from the primal-dual optimization perspective. Our strategy yields a family of algorithms that take the same CTA model as existing algorithms, but they can deal with the non-convex objective, achieve the best possible optimization and communication complexity while being able to deal with both the full batch and mini-batch local computation models. Most importantly, the proposed algorithms are {\it communication efficient}, in the sense that the communication pattern can be adaptive to the level of heterogeneity among the local data. To the best of our knowledge, this is the first algorithmic framework for FL that achieves all the above properties.

Zeroth-Order Regularized Optimization (ZORO): Approximately Sparse Gradients and Adaptive Sampling

We consider the problem of minimizing a high-dimensional objective function, which may include a regularization term, using (possibly noisy) evaluations of the function. Such optimization is also called derivative-free, zeroth-order, or black-box optimization. We propose a new $\textbf{Z}$eroth-$\textbf{O}$rder $\textbf{R}$egularized $\textbf{O}$ptimization method, dubbed ZORO. When the underlying gradient is approximately sparse at an iterate, ZORO needs very few objective function evaluations to obtain a new iterate that decreases the objective function. We achieve this with an adaptive, randomized gradient estimator, followed by an inexact proximal-gradient scheme. Under a novel approximately sparse gradient assumption and various different convex settings, we show the (theoretical and empirical) convergence rate of ZORO is only logarithmically dependent on the problem dimension. Numerical experiments show that ZORO outperforms the existing methods with similar assumptions, on both synthetic and real datasets.