Towards Efficient Optimizer Design for LLM via Structured Fisher Approximation with a Low-Rank Extension

Designing efficient optimizers for large language models (LLMs) with low-memory requirements and fast convergence is an important and challenging problem. This paper makes a step towards the systematic design of such optimizers through the lens of structured Fisher information matrix (FIM) approximation. We show that many state-of-the-art efficient optimizers can be viewed as solutions to FIM approximation (under the Frobenius norm) with specific structural assumptions. Building on these insights, we propose two design recommendations of practical efficient optimizers for LLMs, involving the careful selection of structural assumptions to balance generality and efficiency, and enhancing memory efficiency of optimizers with general structures through a novel low-rank extension framework. We demonstrate how to use each design approach by deriving new memory-efficient optimizers: Row and Column Scaled SGD (RACS) and Adaptive low-dimensional subspace estimation (Alice). Experiments on LLaMA pre-training (up to 1B parameters) validate the effectiveness, showing faster and better convergence than existing memory-efficient baselines and Adam with little memory overhead. Notably, Alice achieves better than 2x faster convergence over Adam, while RACS delivers strong performance on the 1B model with SGD-like memory.

Gradient Multi-Normalization for Stateless and Scalable LLM Training

Training large language models (LLMs) typically relies on adaptive optimizers like Adam (Kingma & Ba, 2015) which store additional state information to accelerate convergence but incur significant memory overhead. Recent efforts, such as SWAN (Ma et al., 2024) address this by eliminating the need for optimizer states while achieving performance comparable to Adam via a multi-step preprocessing procedure applied to instantaneous gradients. Motivated by the success of SWAN, we introduce a novel framework for designing stateless optimizers that normalizes stochastic gradients according to multiple norms. To achieve this, we propose a simple alternating scheme to enforce the normalization of gradients w.r.t these norms. We show that our procedure can produce, up to an arbitrary precision, a fixed-point of the problem, and that SWAN is a particular instance of our approach with carefully chosen norms, providing a deeper understanding of its design. However, SWAN's computationally expensive whitening/orthogonalization step limit its practicality for large LMs. Using our principled perspective, we develop of a more efficient, scalable, and practical stateless optimizer. Our algorithm relaxes the properties of SWAN, significantly reducing its computational cost while retaining its memory efficiency, making it applicable to training large-scale models. Experiments on pre-training LLaMA models with up to 1 billion parameters demonstrate a 3X speedup over Adam with significantly reduced memory requirements, outperforming other memory-efficient baselines.

SWAN: SGD with Normalization and Whitening Enables Stateless LLM Training

Adaptive optimizers such as Adam (Kingma & Ba, 2015) have been central to the success of large language models. However, they often require to maintain optimizer states throughout training, which can result in memory requirements several times greater than the model footprint. This overhead imposes constraints on scalability and computational efficiency. Stochastic Gradient Descent (SGD), in contrast, is a stateless optimizer, as it does not track state variables during training. Consequently, it achieves optimal memory efficiency. However, its capability in LLM training is limited (Zhao et al., 2024b). In this work, we show that pre-processing SGD in a stateless manner can achieve the same performance as the Adam optimizer for LLM training, while drastically reducing the memory cost. Specifically, we propose to pre-process the instantaneous stochastic gradients using normalization and whitening. We show that normalization stabilizes gradient distributions, and whitening counteracts the local curvature of the loss landscape. This results in SWAN (SGD with Whitening And Normalization), a stochastic optimizer that eliminates the need to store any optimizer states. Empirically, SWAN has the same memory footprint as SGD, achieving $\approx 50\%$ reduction on total end-to-end memory compared to Adam. In language modeling tasks, SWAN demonstrates comparable or even better performance than Adam: when pre-training the LLaMA model with 350M and 1.3B parameters, SWAN achieves a 2x speedup by reaching the same evaluation perplexity using half as many tokens.

SWAN: Preprocessing SGD Enables Adam-Level Performance On LLM Training With Significant Memory Reduction

Adaptive optimizers such as Adam (Kingma & Ba, 2015) have been central to the success of large language models. However, they maintain additional moving average states throughout training, which results in memory requirements several times greater than the model. This overhead imposes constraints on scalability and computational efficiency. On the other hand, while stochastic gradient descent (SGD) is optimal in terms of memory efficiency, their capability in LLM training is limited (Zhao et al., 2024b). To address this dilemma, we show that pre-processing SGD is sufficient to reach Adam-level performance on LLMs. Specifically, we propose to preprocess the instantaneous stochastic gradients with two simple operators: $\mathtt{GradNorm}$ and $\mathtt{GradWhitening}$. $\mathtt{GradNorm}$ stabilizes gradient distributions, and $\mathtt{GradWhitening}$ counteracts the local curvature of the loss landscape, respectively. This results in SWAN (SGD with Whitening And Normalization), a stochastic optimizer that eliminates the need to store any accumulative state variables. Empirically, SWAN has the same memory footprint as SGD, achieving $\approx 50\%$ reduction on total end-to-end memory compared to Adam. In language modeling tasks, SWAN demonstrates the same or even a substantial improvement over Adam. Specifically, when pre-training the LLaMa model with 350M and 1.3B parameters, SWAN achieves a 2x speedup by reaching the same evaluation perplexity in less than half tokens seen.

The Essential Role of Causality in Foundation World Models for Embodied AI

Recent advances in foundation models, especially in large multi-modal models and conversational agents, have ignited interest in the potential of generally capable embodied agents. Such agents would require the ability to perform new tasks in many different real-world environments. However, current foundation models fail to accurately model physical interactions with the real world thus not sufficient for Embodied AI. The study of causality lends itself to the construction of veridical world models, which are crucial for accurately predicting the outcomes of possible interactions. This paper focuses on the prospects of building foundation world models for the upcoming generation of embodied agents and presents a novel viewpoint on the significance of causality within these. We posit that integrating causal considerations is vital to facilitate meaningful physical interactions with the world. Finally, we demystify misconceptions about causality in this context and present our outlook for future research.

Neural Structure Learning with Stochastic Differential Equations

Discovering the underlying relationships among variables from temporal observations has been a longstanding challenge in numerous scientific disciplines, including biology, finance, and climate science. The dynamics of such systems are often best described using continuous-time stochastic processes. Unfortunately, most existing structure learning approaches assume that the underlying process evolves in discrete-time and/or observations occur at regular time intervals. These mismatched assumptions can often lead to incorrect learned structures and models. In this work, we introduce a novel structure learning method, SCOTCH, which combines neural stochastic differential equations (SDE) with variational inference to infer a posterior distribution over possible structures. This continuous-time approach can naturally handle both learning from and predicting observations at arbitrary time points. Theoretically, we establish sufficient conditions for an SDE and SCOTCH to be structurally identifiable, and prove its consistency under infinite data limits. Empirically, we demonstrate that our approach leads to improved structure learning performance on both synthetic and real-world datasets compared to relevant baselines under regular and irregular sampling intervals.

BayesDAG: Gradient-Based Posterior Sampling for Causal Discovery

Bayesian causal discovery aims to infer the posterior distribution over causal models from observed data, quantifying epistemic uncertainty and benefiting downstream tasks. However, computational challenges arise due to joint inference over combinatorial space of Directed Acyclic Graphs (DAGs) and nonlinear functions. Despite recent progress towards efficient posterior inference over DAGs, existing methods are either limited to variational inference on node permutation matrices for linear causal models, leading to compromised inference accuracy, or continuous relaxation of adjacency matrices constrained by a DAG regularizer, which cannot ensure resulting graphs are DAGs. In this work, we introduce a scalable Bayesian causal discovery framework based on stochastic gradient Markov Chain Monte Carlo (SG-MCMC) that overcomes these limitations. Our approach directly samples DAGs from the posterior without requiring any DAG regularization, simultaneously draws function parameter samples and is applicable to both linear and nonlinear causal models. To enable our approach, we derive a novel equivalence to the permutation-based DAG learning, which opens up possibilities of using any relaxed gradient estimator defined over permutations. To our knowledge, this is the first framework applying gradient-based MCMC sampling for causal discovery. Empirical evaluations on synthetic and real-world datasets demonstrate our approach's effectiveness compared to state-of-the-art baselines.

Understanding Causality with Large Language Models: Feasibility and Opportunities

We assess the ability of large language models (LLMs) to answer causal questions by analyzing their strengths and weaknesses against three types of causal question. We believe that current LLMs can answer causal questions with existing causal knowledge as combined domain experts. However, they are not yet able to provide satisfactory answers for discovering new knowledge or for high-stakes decision-making tasks with high precision. We discuss possible future directions and opportunities, such as enabling explicit and implicit causal modules as well as deep causal-aware LLMs. These will not only enable LLMs to answer many different types of causal questions for greater impact but also enable LLMs to be more trustworthy and efficient in general.

Rhino: Deep Causal Temporal Relationship Learning With History-dependent Noise

Discovering causal relationships between different variables from time series data has been a long-standing challenge for many domains such as climate science, finance, and healthcare. Given the complexity of real-world relationships and the nature of observations in discrete time, causal discovery methods need to consider non-linear relations between variables, instantaneous effects and history-dependent noise (the change of noise distribution due to past actions). However, previous works do not offer a solution addressing all these problems together. In this paper, we propose a novel causal relationship learning framework for time-series data, called Rhino, which combines vector auto-regression, deep learning and variational inference to model non-linear relationships with instantaneous effects while allowing the noise distribution to be modulated by historical observations. Theoretically, we prove the structural identifiability of Rhino. Our empirical results from extensive synthetic experiments and two real-world benchmarks demonstrate better discovery performance compared to relevant baselines, with ablation studies revealing its robustness under model misspecification.

NeurIPS Competition Instructions and Guide: Causal Insights for Learning Paths in Education

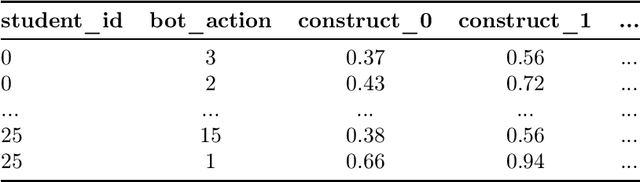
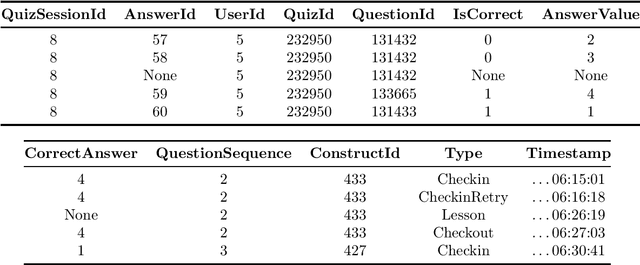
In this competition, participants will address two fundamental causal challenges in machine learning in the context of education using time-series data. The first is to identify the causal relationships between different constructs, where a construct is defined as the smallest element of learning. The second challenge is to predict the impact of learning one construct on the ability to answer questions on other constructs. Addressing these challenges will enable optimisation of students' knowledge acquisition, which can be deployed in a real edtech solution impacting millions of students. Participants will run these tasks in an idealised environment with synthetic data and a real-world scenario with evaluation data collected from a series of A/B tests.