Sampling-based Safe Reinforcement Learning for Nonlinear Dynamical Systems

We develop provably safe and convergent reinforcement learning (RL) algorithms for control of nonlinear dynamical systems, bridging the gap between the hard safety guarantees of control theory and the convergence guarantees of RL theory. Recent advances at the intersection of control and RL follow a two-stage, safety filter approach to enforcing hard safety constraints: model-free RL is used to learn a potentially unsafe controller, whose actions are projected onto safe sets prescribed, for example, by a control barrier function. Though safe, such approaches lose any convergence guarantees enjoyed by the underlying RL methods. In this paper, we develop a single-stage, sampling-based approach to hard constraint satisfaction that learns RL controllers enjoying classical convergence guarantees while satisfying hard safety constraints throughout training and deployment. We validate the efficacy of our approach in simulation, including safe control of a quadcopter in a challenging obstacle avoidance problem, and demonstrate that it outperforms existing benchmarks.

Towards Model-Free LQR Control over Rate-Limited Channels

Given the success of model-free methods for control design in many problem settings, it is natural to ask how things will change if realistic communication channels are utilized for the transmission of gradients or policies. While the resulting problem has analogies with the formulations studied under the rubric of networked control systems, the rich literature in that area has typically assumed that the model of the system is known. As a step towards bridging the fields of model-free control design and networked control systems, we ask: \textit{Is it possible to solve basic control problems - such as the linear quadratic regulator (LQR) problem - in a model-free manner over a rate-limited channel?} Toward answering this question, we study a setting where a worker agent transmits quantized policy gradients (of the LQR cost) to a server over a noiseless channel with a finite bit-rate. We propose a new algorithm titled Adaptively Quantized Gradient Descent (\texttt{AQGD}), and prove that above a certain finite threshold bit-rate, \texttt{AQGD} guarantees exponentially fast convergence to the globally optimal policy, with \textit{no deterioration of the exponent relative to the unquantized setting}. More generally, our approach reveals the benefits of adaptive quantization in preserving fast linear convergence rates, and, as such, may be of independent interest to the literature on compressed optimization.

Intrinsic and extrinsic deep learning on manifolds

We propose extrinsic and intrinsic deep neural network architectures as general frameworks for deep learning on manifolds. Specifically, extrinsic deep neural networks (eDNNs) preserve geometric features on manifolds by utilizing an equivariant embedding from the manifold to its image in the Euclidean space. Moreover, intrinsic deep neural networks (iDNNs) incorporate the underlying intrinsic geometry of manifolds via exponential and log maps with respect to a Riemannian structure. Consequently, we prove that the empirical risk of the empirical risk minimizers (ERM) of eDNNs and iDNNs converge in optimal rates. Overall, The eDNNs framework is simple and easy to compute, while the iDNNs framework is accurate and fast converging. To demonstrate the utilities of our framework, various simulation studies, and real data analyses are presented with eDNNs and iDNNs.

Regret Bounds for Learning Decentralized Linear Quadratic Regulator with Partially Nested Information Structure

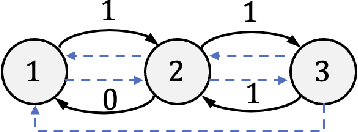
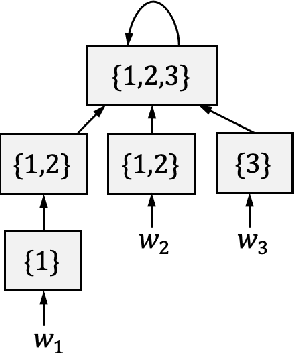
We study the problem of learning decentralized linear quadratic regulator under a partially nested information constraint, when the system model is unknown a priori. We propose an online learning algorithm that adaptively designs a control policy as new data samples from a single system trajectory become available. Our algorithm design uses a disturbance-feedback representation of state-feedback controllers coupled with online convex optimization with memory and delayed feedback. We show that our online algorithm yields a controller that satisfies the desired information constraint and enjoys an expected regret that scales as $\sqrt{T}$ with the time horizon $T$.

Cooperative Actor-Critic via TD Error Aggregation

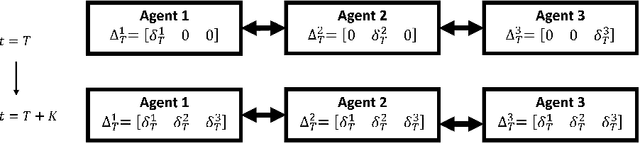
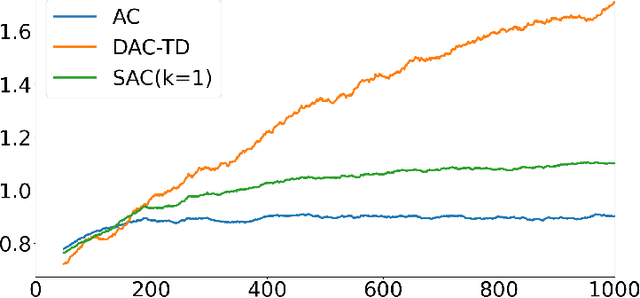
In decentralized cooperative multi-agent reinforcement learning, agents can aggregate information from one another to learn policies that maximize a team-average objective function. Despite the willingness to cooperate with others, the individual agents may find direct sharing of information about their local state, reward, and value function undesirable due to privacy issues. In this work, we introduce a decentralized actor-critic algorithm with TD error aggregation that does not violate privacy issues and assumes that communication channels are subject to time delays and packet dropouts. The cost we pay for making such weak assumptions is an increased communication burden for every agent as measured by the dimension of the transmitted data. Interestingly, the communication burden is only quadratic in the graph size, which renders the algorithm applicable in large networks. We provide a convergence analysis under diminishing step size to verify that the agents maximize the team-average objective function.

Robustness against Adversarial Attacks in Neural Networks using Incremental Dissipativity

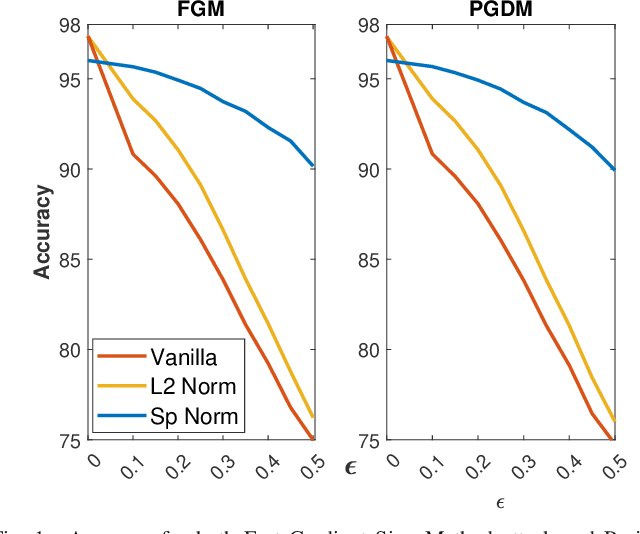
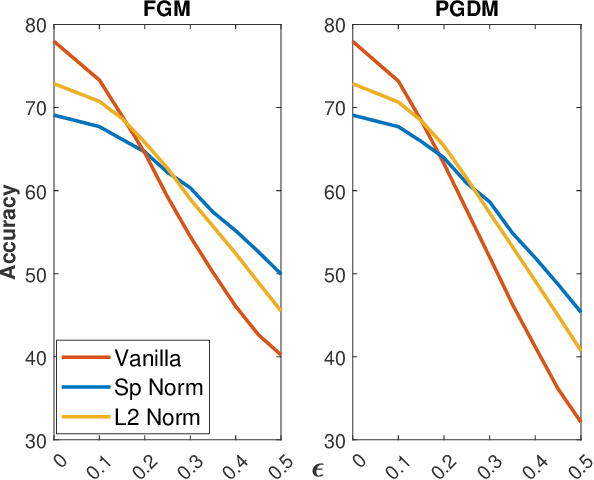
Adversarial examples can easily degrade the classification performance in neural networks. Empirical methods for promoting robustness to such examples have been proposed, but often lack both analytical insights and formal guarantees. Recently, some robustness certificates have appeared in the literature based on system theoretic notions. This work proposes an incremental dissipativity-based robustness certificate for neural networks in the form of a linear matrix inequality for each layer. We also propose an equivalent spectral norm bound for this certificate which is scalable to neural networks with multiple layers. We demonstrate the improved performance against adversarial attacks on a feed-forward neural network trained on MNIST and an Alexnet trained using CIFAR-10.

Finite-Time Error Bounds for Distributed Linear Stochastic Approximation

This paper considers a novel multi-agent linear stochastic approximation algorithm driven by Markovian noise and general consensus-type interaction, in which each agent evolves according to its local stochastic approximation process which depends on the information from its neighbors. The interconnection structure among the agents is described by a time-varying directed graph. While the convergence of consensus-based stochastic approximation algorithms when the interconnection among the agents is described by doubly stochastic matrices (at least in expectation) has been studied, less is known about the case when the interconnection matrix is simply stochastic. For any uniformly strongly connected graph sequences whose associated interaction matrices are stochastic, the paper derives finite-time bounds on the mean-square error, defined as the deviation of the output of the algorithm from the unique equilibrium point of the associated ordinary differential equation. For the case of interconnection matrices being stochastic, the equilibrium point can be any unspecified convex combination of the local equilibria of all the agents in the absence of communication. Both the cases with constant and time-varying step-sizes are considered. In the case when the convex combination is required to be a straight average and interaction between any pair of neighboring agents may be uni-directional, so that doubly stochastic matrices cannot be implemented in a distributed manner, the paper proposes a push-sum-type distributed stochastic approximation algorithm and provides its finite-time bound for the time-varying step-size case by leveraging the analysis for the consensus-type algorithm with stochastic matrices and developing novel properties of the push-sum algorithm.

Resilient Consensus-based Multi-agent Reinforcement Learning with Function Approximation

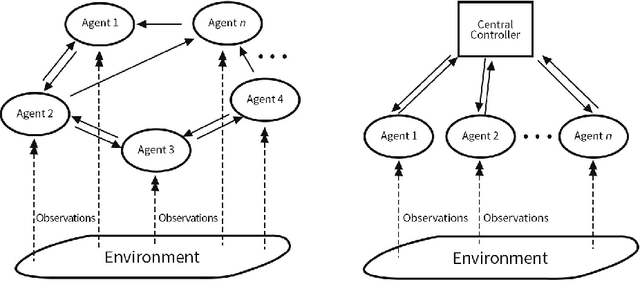
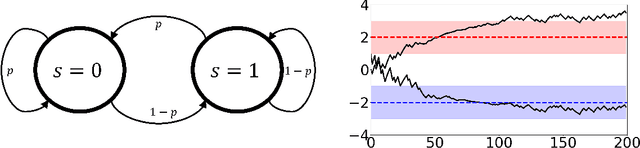
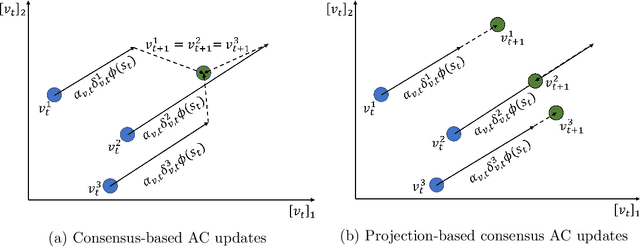
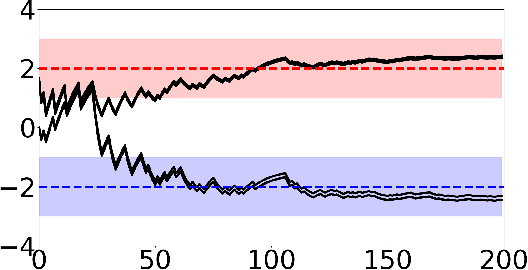
Adversarial attacks during training can strongly influence the performance of multi-agent reinforcement learning algorithms. It is, thus, highly desirable to augment existing algorithms such that the impact of adversarial attacks on cooperative networks is eliminated, or at least bounded. In this work, we consider a fully decentralized network, where each agent receives a local reward and observes the global state and action. We propose a resilient consensus-based actor-critic algorithm, whereby each agent estimates the team-average reward and value function, and communicates the associated parameter vectors to its immediate neighbors. We show that in the presence of Byzantine agents, whose estimation and communication strategies are completely arbitrary, the estimates of the cooperative agents converge to a bounded consensus value with probability one, provided that there are at most $H$ Byzantine agents in the neighborhood of each cooperative agent and the network is $(2H+1)$-robust. Furthermore, we prove that the policy of the cooperative agents converges with probability one to a bounded neighborhood around a local maximizer of their team-average objective function under the assumption that the policies of the adversarial agents asymptotically become stationary.

On the Sample Complexity of Decentralized Linear Quadratic Regulator with Partially Nested Information Structure

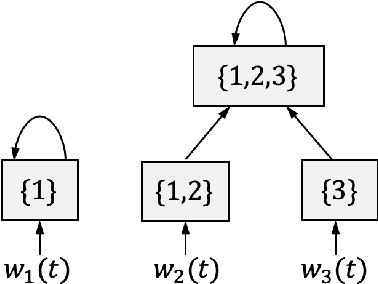
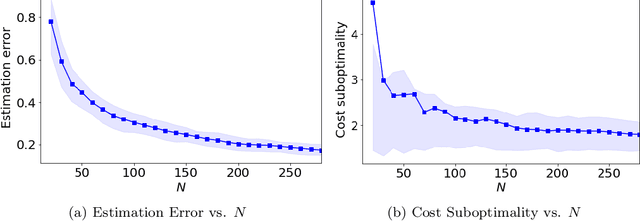
We study the problem of control policy design for decentralized state-feedback linear quadratic control with a partially nested information structure, when the system model is unknown. We propose a model-based learning solution, which consists of two steps. First, we estimate the unknown system model from a single system trajectory of finite length, using least squares estimation. Next, based on the estimated system model, we design a control policy that satisfies the desired information structure. We show that the suboptimality gap between our control policy and the optimal decentralized control policy (designed using accurate knowledge of the system model) scales linearly with the estimation error of the system model. Using this result, we provide an end-to-end sample complexity result for learning decentralized controllers for a linear quadratic control problem with a partially nested information structure.

Data-Driven Contract Design for Multi-Agent Systems with Collusion Detection

In applications such as participatory sensing and crowd sensing, self-interested agents exert costly effort towards achieving an objective for the system operator. We study such a setup where a principal incentivizes multiple agents of different types who can collude with each other to derive rent. The principal cannot observe the efforts exerted directly, but only the outcome of the task, which is a noisy function of the effort. The type of each agent influences the effort cost and task output. For a duopoly in which agents are coupled in their payments, we show that if the principal and the agents interact finitely many times, the agents can derive rent by colluding even if the principal knows the types of the agents. However, if the principal and the agents interact infinitely often, the principal can disincentivize agent collusion through a suitable data-driven contract.