Cooperative Actor-Critic via TD Error Aggregation

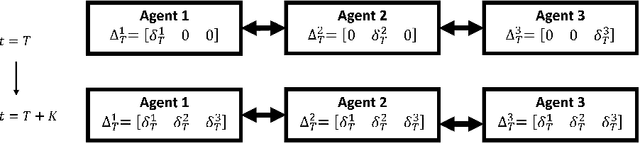
In decentralized cooperative multi-agent reinforcement learning, agents can aggregate information from one another to learn policies that maximize a team-average objective function. Despite the willingness to cooperate with others, the individual agents may find direct sharing of information about their local state, reward, and value function undesirable due to privacy issues. In this work, we introduce a decentralized actor-critic algorithm with TD error aggregation that does not violate privacy issues and assumes that communication channels are subject to time delays and packet dropouts. The cost we pay for making such weak assumptions is an increased communication burden for every agent as measured by the dimension of the transmitted data. Interestingly, the communication burden is only quadratic in the graph size, which renders the algorithm applicable in large networks. We provide a convergence analysis under diminishing step size to verify that the agents maximize the team-average objective function.

Finite-Time Error Bounds for Distributed Linear Stochastic Approximation

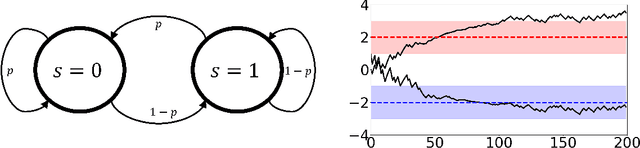
This paper considers a novel multi-agent linear stochastic approximation algorithm driven by Markovian noise and general consensus-type interaction, in which each agent evolves according to its local stochastic approximation process which depends on the information from its neighbors. The interconnection structure among the agents is described by a time-varying directed graph. While the convergence of consensus-based stochastic approximation algorithms when the interconnection among the agents is described by doubly stochastic matrices (at least in expectation) has been studied, less is known about the case when the interconnection matrix is simply stochastic. For any uniformly strongly connected graph sequences whose associated interaction matrices are stochastic, the paper derives finite-time bounds on the mean-square error, defined as the deviation of the output of the algorithm from the unique equilibrium point of the associated ordinary differential equation. For the case of interconnection matrices being stochastic, the equilibrium point can be any unspecified convex combination of the local equilibria of all the agents in the absence of communication. Both the cases with constant and time-varying step-sizes are considered. In the case when the convex combination is required to be a straight average and interaction between any pair of neighboring agents may be uni-directional, so that doubly stochastic matrices cannot be implemented in a distributed manner, the paper proposes a push-sum-type distributed stochastic approximation algorithm and provides its finite-time bound for the time-varying step-size case by leveraging the analysis for the consensus-type algorithm with stochastic matrices and developing novel properties of the push-sum algorithm.

Resilient Consensus-based Multi-agent Reinforcement Learning with Function Approximation

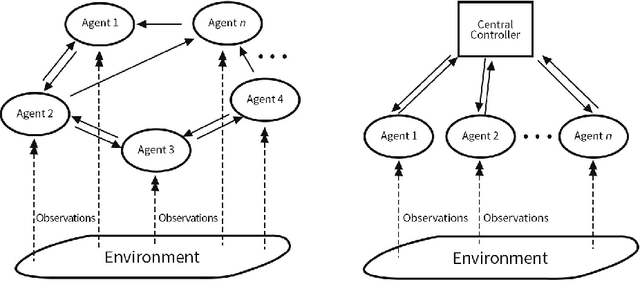
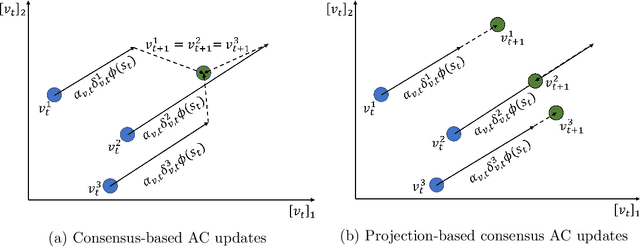
Adversarial attacks during training can strongly influence the performance of multi-agent reinforcement learning algorithms. It is, thus, highly desirable to augment existing algorithms such that the impact of adversarial attacks on cooperative networks is eliminated, or at least bounded. In this work, we consider a fully decentralized network, where each agent receives a local reward and observes the global state and action. We propose a resilient consensus-based actor-critic algorithm, whereby each agent estimates the team-average reward and value function, and communicates the associated parameter vectors to its immediate neighbors. We show that in the presence of Byzantine agents, whose estimation and communication strategies are completely arbitrary, the estimates of the cooperative agents converge to a bounded consensus value with probability one, provided that there are at most $H$ Byzantine agents in the neighborhood of each cooperative agent and the network is $(2H+1)$-robust. Furthermore, we prove that the policy of the cooperative agents converges with probability one to a bounded neighborhood around a local maximizer of their team-average objective function under the assumption that the policies of the adversarial agents asymptotically become stationary.

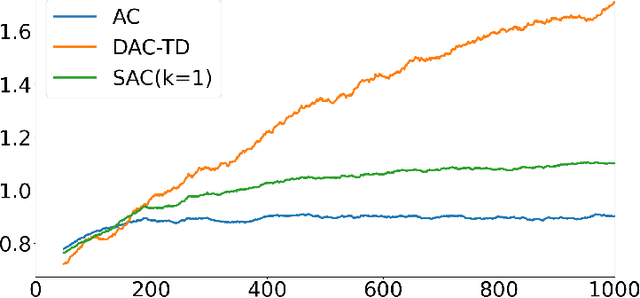
A Communication-Efficient Multi-Agent Actor-Critic Algorithm for Distributed Reinforcement Learning

This paper considers a distributed reinforcement learning problem in which a network of multiple agents aim to cooperatively maximize the globally averaged return through communication with only local neighbors. A randomized communication-efficient multi-agent actor-critic algorithm is proposed for possibly unidirectional communication relationships depicted by a directed graph. It is shown that the algorithm can solve the problem for strongly connected graphs by allowing each agent to transmit only two scalar-valued variables at one time.