Sparse Feature Selection Makes Batch Reinforcement Learning More Sample Efficient

This paper provides a statistical analysis of high-dimensional batch Reinforcement Learning (RL) using sparse linear function approximation. When there is a large number of candidate features, our result sheds light on the fact that sparsity-aware methods can make batch RL more sample efficient. We first consider the off-policy policy evaluation problem. To evaluate a new target policy, we analyze a Lasso fitted Q-evaluation method and establish a finite-sample error bound that has no polynomial dependence on the ambient dimension. To reduce the Lasso bias, we further propose a post model-selection estimator that applies fitted Q-evaluation to the features selected via group Lasso. Under an additional signal strength assumption, we derive a sharper instance-dependent error bound that depends on a divergence function measuring the distribution mismatch between the data distribution and occupancy measure of the target policy. Further, we study the Lasso fitted Q-iteration for batch policy optimization and establish a finite-sample error bound depending on the ratio between the number of relevant features and restricted minimal eigenvalue of the data's covariance. In the end, we complement the results with minimax lower bounds for batch-data policy evaluation/optimization that nearly match our upper bounds. The results suggest that having well-conditioned data is crucial for sparse batch policy learning.

Online Sparse Reinforcement Learning

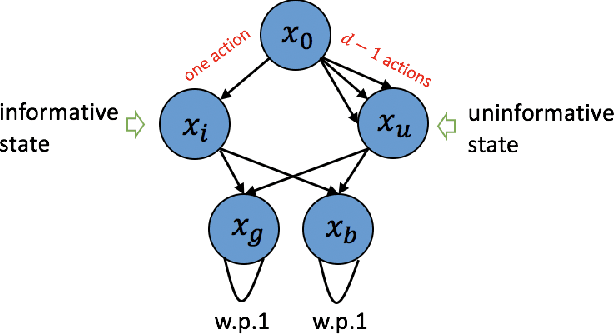
We investigate the hardness of online reinforcement learning in sparse linear Markov decision process (MDP), with a special focus on the high-dimensional regime where the ambient dimension is larger than the number of episodes. Our contribution is two-fold. First, we provide a lower bound showing that linear regret is generally unavoidable, even if there exists a policy that collects well-conditioned data. Second, we show that if the learner has oracle access to a policy that collects well-conditioned data, then a variant of Lasso fitted Q-iteration enjoys a regret of $\tilde{O}(N^{2/3})$ where $N$ is the number of episodes.

Mirror Descent and the Information Ratio

We establish a connection between the stability of mirror descent and the information ratio by Russo and Van Roy [2014]. Our analysis shows that mirror descent with suitable loss estimators and exploratory distributions enjoys the same bound on the adversarial regret as the bounds on the Bayesian regret for information-directed sampling. Along the way, we develop the theory for information-directed sampling and provide an efficient algorithm for adversarial bandits for which the regret upper bound matches exactly the best known information-theoretic upper bound.

Improved Regret for Zeroth-Order Adversarial Bandit Convex Optimisation

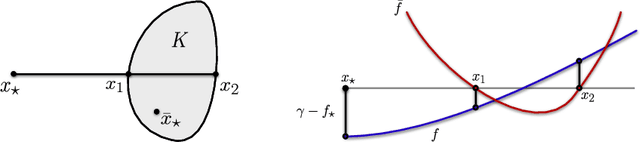
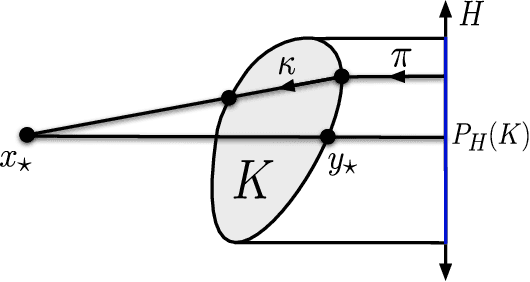
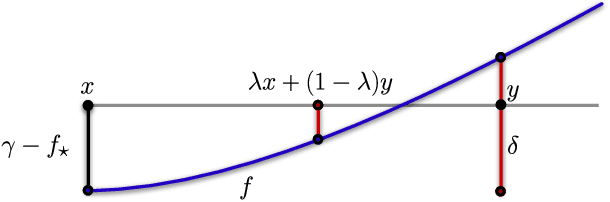
We prove that the information-theoretic upper bound on the minimax regret for zeroth-order adversarial bandit convex optimisation is at most $O(d^{2.5} \sqrt{n} \log(n))$, where $d$ is the dimension and $n$ is the number of interactions. This improves on $O(d^{9.5} \sqrt{n} \log(n)^{7.5}$ by Bubeck et al. (2017). The proof is based on identifying an improved exploratory distribution for convex functions.

Gaussian Gated Linear Networks

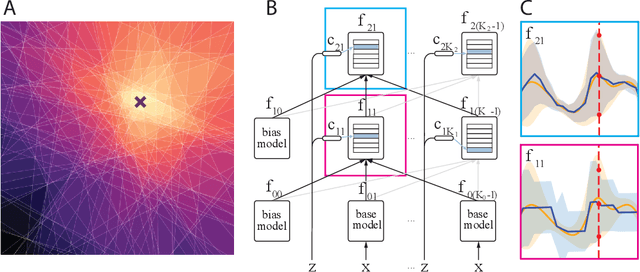
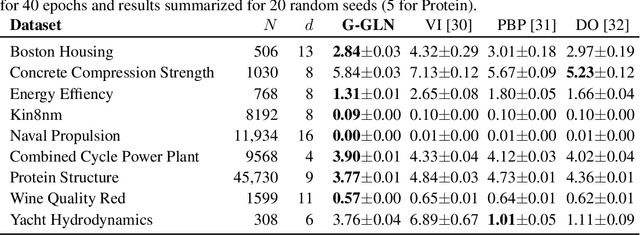
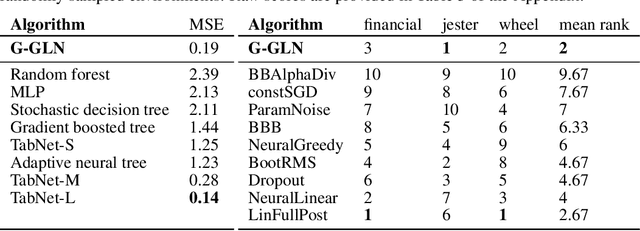
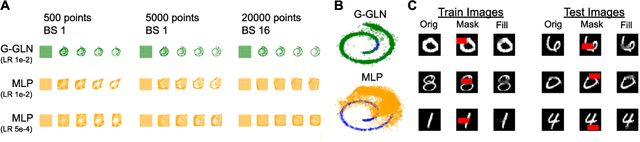
We propose the Gaussian Gated Linear Network (G-GLN), an extension to the recently proposed GLN family of deep neural networks. Instead of using backpropagation to learn features, GLNs have a distributed and local credit assignment mechanism based on optimizing a convex objective. This gives rise to many desirable properties including universality, data-efficient online learning, trivial interpretability and robustness to catastrophic forgetting. We extend the GLN framework from classification to multiple regression and density modelling by generalizing geometric mixing to a product of Gaussian densities. The G-GLN achieves competitive or state-of-the-art performance on several univariate and multivariate regression benchmarks, and we demonstrate its applicability to practical tasks including online contextual bandits and density estimation via denoising.

Stochastic matrix games with bandit feedback

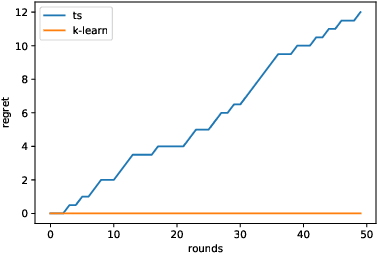
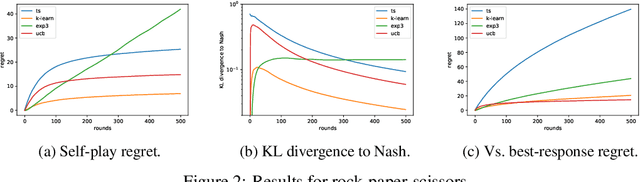
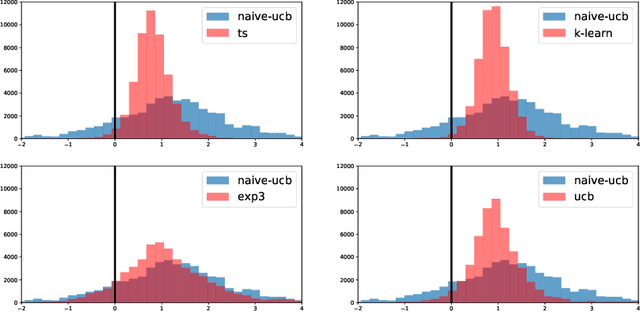
We study a version of the classical zero-sum matrix game with unknown payoff matrix and bandit feedback, where the players only observe each others actions and a noisy payoff. This generalizes the usual matrix game, where the payoff matrix is known to the players. Despite numerous applications, this problem has received relatively little attention. Although adversarial bandit algorithms achieve low regret, they do not exploit the matrix structure and perform poorly relative to the new algorithms. The main contributions are regret analyses of variants of UCB and K-learning that hold for any opponent, e.g., even when the opponent adversarially plays the best response to the learner's mixed strategy. Along the way, we show that Thompson fails catastrophically in this setting and provide empirical comparison to existing algorithms.

Model Selection in Contextual Stochastic Bandit Problems

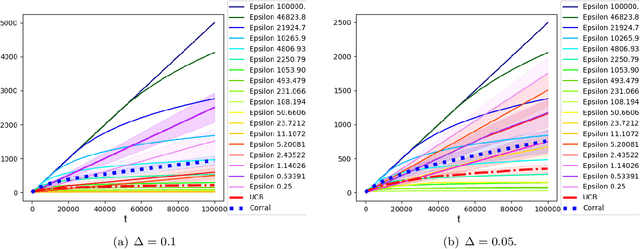
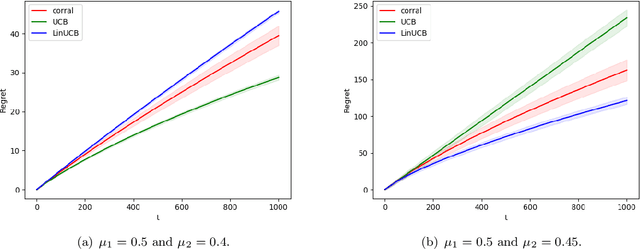
We study model selection in stochastic bandit problems. Our approach relies on a master algorithm that selects its actions among candidate base algorithms. While this problem is studied for specific classes of stochastic base algorithms, our objective is to provide a method that can work with more general classes of stochastic base algorithms. We propose a master algorithm inspired by CORRAL \cite{DBLP:conf/colt/AgarwalLNS17} and introduce a novel and generic smoothing transformation for stochastic bandit algorithms that permits us to obtain $O(\sqrt{T})$ regret guarantees for a wide class of base algorithms when working along with our master. We exhibit a lower bound showing that even when one of the base algorithms has $O(\log T)$ regret, in general it is impossible to get better than $\Omega(\sqrt{T})$ regret in model selection, even asymptotically. We apply our algorithm to choose among different values of $\epsilon$ for the $\epsilon$-greedy algorithm, and to choose between the $k$-armed UCB and linear UCB algorithms. Our empirical studies further confirm the effectiveness of our model-selection method.

Information Directed Sampling for Linear Partial Monitoring

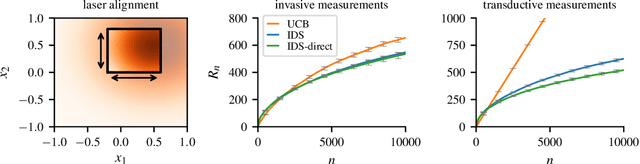
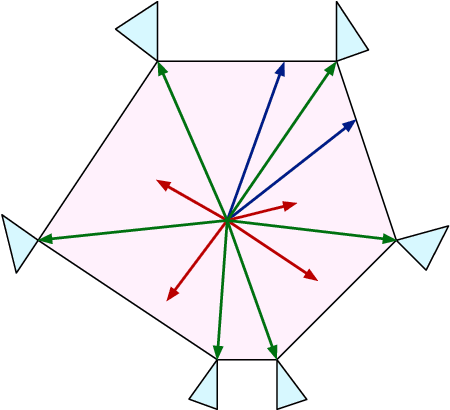
Partial monitoring is a rich framework for sequential decision making under uncertainty that generalizes many well known bandit models, including linear, combinatorial and dueling bandits. We introduce information directed sampling (IDS) for stochastic partial monitoring with a linear reward and observation structure. IDS achieves adaptive worst-case regret rates that depend on precise observability conditions of the game. Moreover, we prove lower bounds that classify the minimax regret of all finite games into four possible regimes. IDS achieves the optimal rate in all cases up to logarithmic factors, without tuning any hyper-parameters. We further extend our results to the contextual and the kernelized setting, which significantly increases the range of possible applications.

Learning with Good Feature Representations in Bandits and in RL with a Generative Model

The construction in the recent paper by Du et al. [2019] implies that searching for a near-optimal action in a bandit sometimes requires examining essentially all the actions, even if the learner is given linear features in $\mathbb R^d$ that approximate the rewards with a small uniform error. In this note we use the Kiefer-Wolfowitz theorem to show that by checking only a few actions, a learner can always find an action which is suboptimal with an error of at most $O(\varepsilon \sqrt{d})$ where $\varepsilon$ is the approximation error of the features. Thus, features are useful when the approximation error is small relative to the dimensionality of the features. The idea is applied to stochastic bandits and reinforcement learning with a generative model where the learner has access to $d$-dimensional linear features that approximate the action-value functions for all policies to an accuracy of $\varepsilon$. For bandits we prove a bound on the regret of order $\sqrt{dn \log(k)} + \varepsilon n \sqrt{d} \log(n)$ with $k$ the number of actions and $n$ the horizon. For RL we show that approximate policy iteration can learn a policy that is optimal up to an additive error of order $\varepsilon \sqrt{d} / (1 - \gamma)^2$ and using about $d / (\varepsilon^2(1-\gamma)^4)$ samples from the generative model.

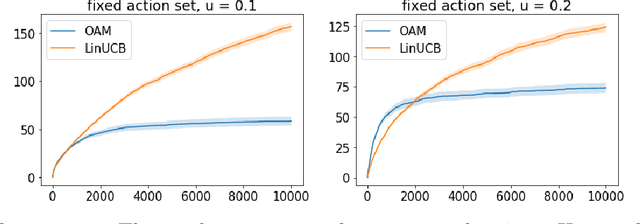
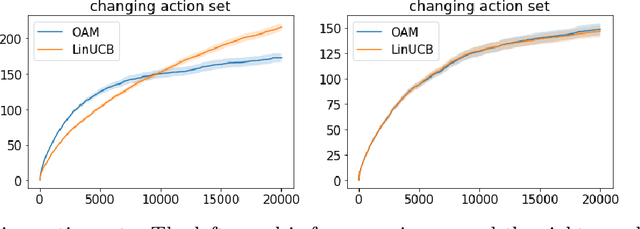
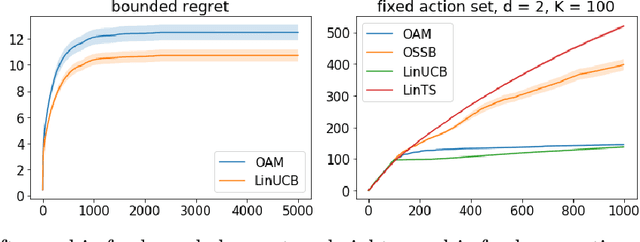
Adaptive Exploration in Linear Contextual Bandit

Contextual bandits serve as a fundamental model for many sequential decision making tasks. The most popular theoretically justified approaches are based on the optimism principle. While these algorithms can be practical, they are known to be suboptimal asymptotically (Lattimore and Szepesvari, 2017). On the other hand, existing asymptotically optimal algorithms for this problem do not exploit the linear structure in an optimal way and suffer from lower-order terms that dominate the regret in all practically interesting regimes. We start to bridge the gap by designing an algorithm that is asymptotically optimal and has good finite-time empirical performance. At the same time, we make connections to the recent literature on when exploration-free methods are effective. Indeed, if the distribution of contexts is well behaved, then our algorithm acts mostly greedily and enjoys sub-logarithmic regret. Furthermore, our approach is adaptive in the sense that it automatically detects the nice case. Numerical results demonstrate significant regret reductions by our method relative to several baselines.