Improved Regret for Zeroth-Order Adversarial Bandit Convex Optimisation
Paper and Code
Jun 19, 2020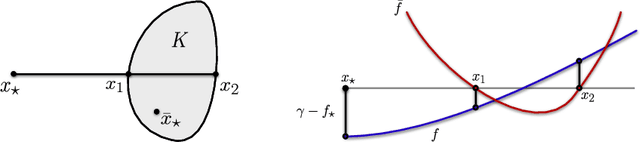
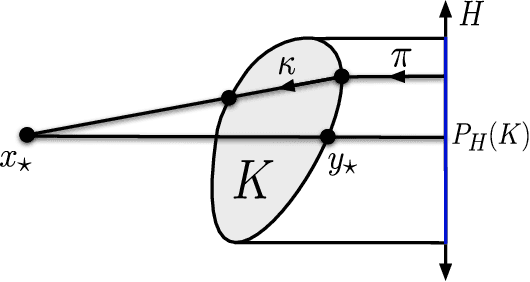
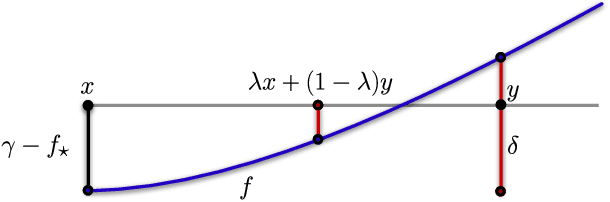
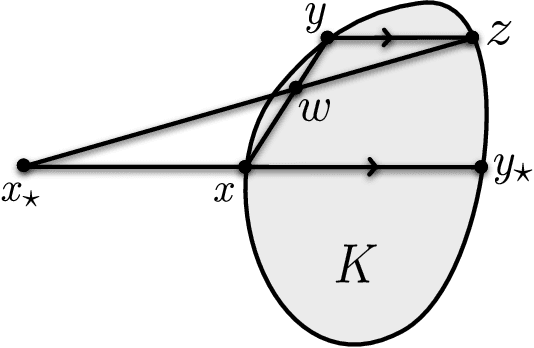
We prove that the information-theoretic upper bound on the minimax regret for zeroth-order adversarial bandit convex optimisation is at most $O(d^{2.5} \sqrt{n} \log(n))$, where $d$ is the dimension and $n$ is the number of interactions. This improves on $O(d^{9.5} \sqrt{n} \log(n)^{7.5}$ by Bubeck et al. (2017). The proof is based on identifying an improved exploratory distribution for convex functions.
* 20 pages, 5 figures. Bound is now improved by d^{1/2}
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge