Gradual Transition from Bellman Optimality Operator to Bellman Operator in Online Reinforcement Learning

For continuous action spaces, actor-critic methods are widely used in online reinforcement learning (RL). However, unlike RL algorithms for discrete actions, which generally model the optimal value function using the Bellman optimality operator, RL algorithms for continuous actions typically model Q-values for the current policy using the Bellman operator. These algorithms for continuous actions rely exclusively on policy updates for improvement, which often results in low sample efficiency. This study examines the effectiveness of incorporating the Bellman optimality operator into actor-critic frameworks. Experiments in a simple environment show that modeling optimal values accelerates learning but leads to overestimation bias. To address this, we propose an annealing approach that gradually transitions from the Bellman optimality operator to the Bellman operator, thereby accelerating learning while mitigating bias. Our method, combined with TD3 and SAC, significantly outperforms existing approaches across various locomotion and manipulation tasks, demonstrating improved performance and robustness to hyperparameters related to optimality.

Discovering Multiple Solutions from a Single Task in Offline Reinforcement Learning

Recent studies on online reinforcement learning (RL) have demonstrated the advantages of learning multiple behaviors from a single task, as in the case of few-shot adaptation to a new environment. Although this approach is expected to yield similar benefits in offline RL, appropriate methods for learning multiple solutions have not been fully investigated in previous studies. In this study, we therefore addressed the problem of finding multiple solutions from a single task in offline RL. We propose algorithms that can learn multiple solutions in offline RL, and empirically investigate their performance. Our experimental results show that the proposed algorithm learns multiple qualitatively and quantitatively distinctive solutions in offline RL.

Stabilizing Extreme Q-learning by Maclaurin Expansion

In Extreme Q-learning (XQL), Gumbel Regression is performed with an assumed Gumbel distribution for the error distribution. This allows learning of the value function without sampling out-of-distribution actions and has shown excellent performance mainly in Offline RL. However, issues remained, including the exponential term in the loss function causing instability and the potential for an error distribution diverging from the Gumbel distribution. Therefore, we propose Maclaurin Expanded Extreme Q-learning to enhance stability. In this method, applying Maclaurin expansion to the loss function in XQL enhances stability against large errors. It also allows adjusting the error distribution assumption from normal to Gumbel based on the expansion order. Our method significantly stabilizes learning in Online RL tasks from DM Control, where XQL was previously unstable. Additionally, it improves performance in several Offline RL tasks from D4RL, where XQL already showed excellent results.

Offline Reinforcement Learning from Datasets with Structured Non-Stationarity

Current Reinforcement Learning (RL) is often limited by the large amount of data needed to learn a successful policy. Offline RL aims to solve this issue by using transitions collected by a different behavior policy. We address a novel Offline RL problem setting in which, while collecting the dataset, the transition and reward functions gradually change between episodes but stay constant within each episode. We propose a method based on Contrastive Predictive Coding that identifies this non-stationarity in the offline dataset, accounts for it when training a policy, and predicts it during evaluation. We analyze our proposed method and show that it performs well in simple continuous control tasks and challenging, high-dimensional locomotion tasks. We show that our method often achieves the oracle performance and performs better than baselines.

Symmetric Q-learning: Reducing Skewness of Bellman Error in Online Reinforcement Learning

In deep reinforcement learning, estimating the value function to evaluate the quality of states and actions is essential. The value function is often trained using the least squares method, which implicitly assumes a Gaussian error distribution. However, a recent study suggested that the error distribution for training the value function is often skewed because of the properties of the Bellman operator, and violates the implicit assumption of normal error distribution in the least squares method. To address this, we proposed a method called Symmetric Q-learning, in which the synthetic noise generated from a zero-mean distribution is added to the target values to generate a Gaussian error distribution. We evaluated the proposed method on continuous control benchmark tasks in MuJoCo. It improved the sample efficiency of a state-of-the-art reinforcement learning method by reducing the skewness of the error distribution.

Open X-Embodiment: Robotic Learning Datasets and RT-X Models

Large, high-capacity models trained on diverse datasets have shown remarkable successes on efficiently tackling downstream applications. In domains from NLP to Computer Vision, this has led to a consolidation of pretrained models, with general pretrained backbones serving as a starting point for many applications. Can such a consolidation happen in robotics? Conventionally, robotic learning methods train a separate model for every application, every robot, and even every environment. Can we instead train generalist X-robot policy that can be adapted efficiently to new robots, tasks, and environments? In this paper, we provide datasets in standardized data formats and models to make it possible to explore this possibility in the context of robotic manipulation, alongside experimental results that provide an example of effective X-robot policies. We assemble a dataset from 22 different robots collected through a collaboration between 21 institutions, demonstrating 527 skills (160266 tasks). We show that a high-capacity model trained on this data, which we call RT-X, exhibits positive transfer and improves the capabilities of multiple robots by leveraging experience from other platforms. More details can be found on the project website $\href{https://robotics-transformer-x.github.io}{\text{robotics-transformer-x.github.io}}$.

Motion Planning by Learning the Solution Manifold in Trajectory Optimization

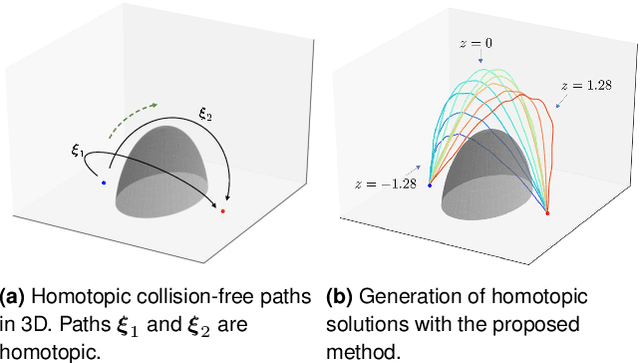
The objective function used in trajectory optimization is often non-convex and can have an infinite set of local optima. In such cases, there are diverse solutions to perform a given task. Although there are a few methods to find multiple solutions for motion planning, they are limited to generating a finite set of solutions. To address this issue, we presents an optimization method that learns an infinite set of solutions in trajectory optimization. In our framework, diverse solutions are obtained by learning latent representations of solutions. Our approach can be interpreted as training a deep generative model of collision-free trajectories for motion planning. The experimental results indicate that the trained model represents an infinite set of homotopic solutions for motion planning problems.

Discovering Diverse Solutions in Deep Reinforcement Learning

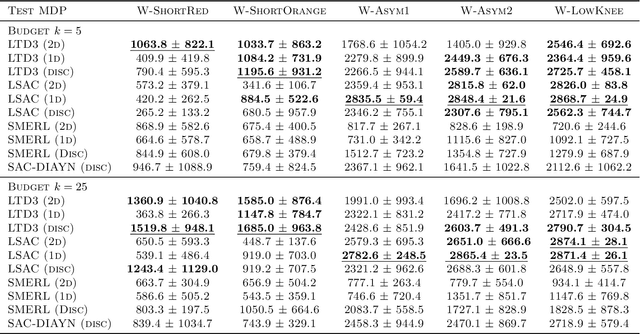
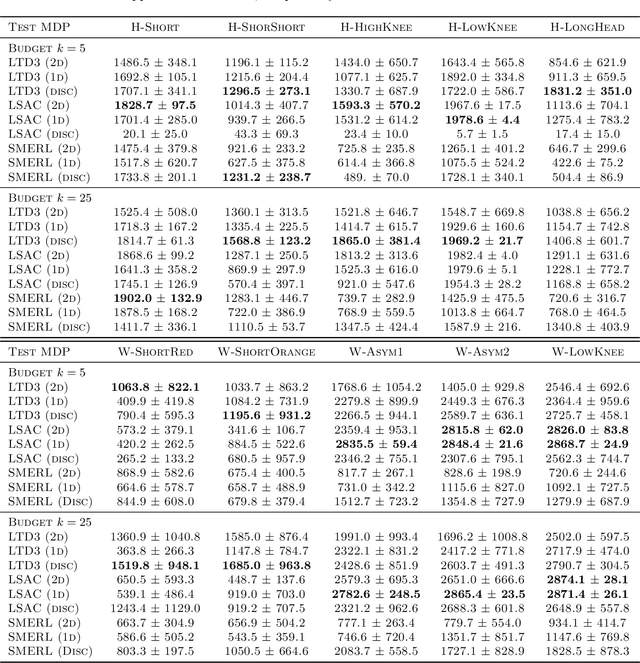
Reinforcement learning (RL) algorithms are typically limited to learning a single solution of a specified task, even though there often exists diverse solutions to a given task. Compared with learning a single solution, learning a set of diverse solutions is beneficial because diverse solutions enable robust few-shot adaptation and allow the user to select a preferred solution. Although previous studies have showed that diverse behaviors can be modeled with a policy conditioned on latent variables, an approach for modeling an infinite set of diverse solutions with continuous latent variables has not been investigated. In this study, we propose an RL method that can learn infinitely many solutions by training a policy conditioned on a continuous or discrete low-dimensional latent variable. Through continuous control tasks, we demonstrate that our method can learn diverse solutions in a data-efficient manner and that the solutions can be used for few-shot adaptation to solve unseen tasks.

Learning the Solution Manifold in Optimization and Its Application in Motion Planning

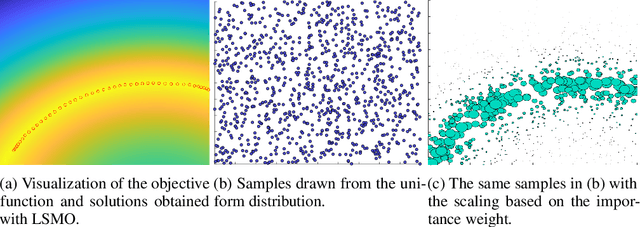
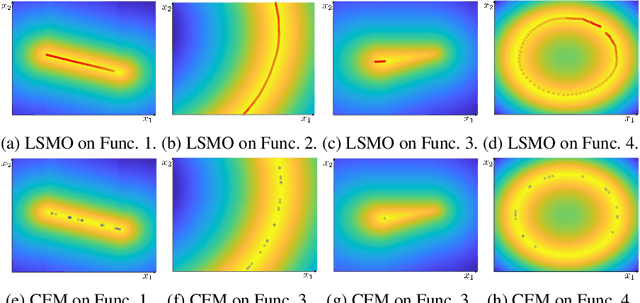
Optimization is an essential component for solving problems in wide-ranging fields. Ideally, the objective function should be designed such that the solution is unique and the optimization problem can be solved stably. However, the objective function used in a practical application is usually non-convex, and sometimes it even has an infinite set of solutions. To address this issue, we propose to learn the solution manifold in optimization. We train a model conditioned on the latent variable such that the model represents an infinite set of solutions. In our framework, we reduce this problem to density estimation by using importance sampling, and the latent representation of the solutions is learned by maximizing the variational lower bound. We apply the proposed algorithm to motion-planning problems, which involve the optimization of high-dimensional parameters. The experimental results indicate that the solution manifold can be learned with the proposed algorithm, and the trained model represents an infinite set of homotopic solutions for motion-planning problems.

Meta-Model-Based Meta-Policy Optimization

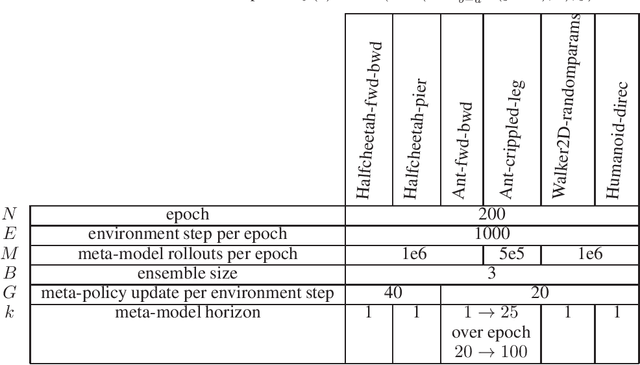
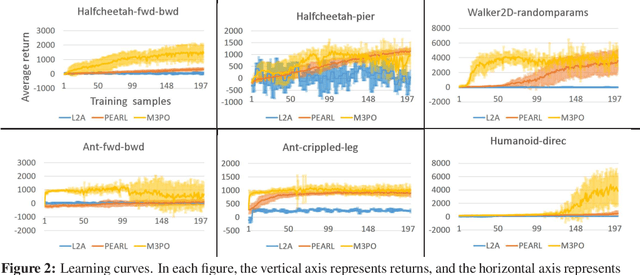
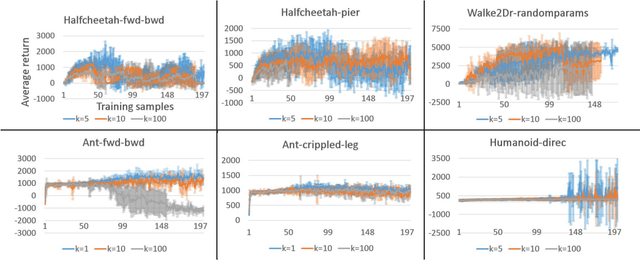
Model-based reinforcement learning (MBRL) has been applied to meta-learning settings and demonstrated its high sample efficiency. However, in previous MBRL for meta-learning settings, policies are optimized via rollouts that fully rely on a predictive model for an environment, and thus its performance in a real environment tends to degrade when the predictive model is inaccurate. In this paper, we prove that the performance degradation can be suppressed by using branched meta-rollouts. Based on this theoretical analysis, we propose meta-model-based meta-policy optimization (M3PO), in which the branched meta-rollouts are used for policy optimization. We demonstrate that M3PO outperforms existing meta reinforcement learning methods in continuous-control benchmarks.