Improved Sample Complexity of Imitation Learning for Barrier Model Predictive Control

Recent work in imitation learning has shown that having an expert controller that is both suitably smooth and stable enables stronger guarantees on the performance of the learned controller. However, constructing such smoothed expert controllers for arbitrary systems remains challenging, especially in the presence of input and state constraints. As our primary contribution, we show how such a smoothed expert can be designed for a general class of systems using a log-barrier-based relaxation of a standard Model Predictive Control (MPC) optimization problem. Improving upon our previous work, we show that barrier MPC achieves theoretically optimal error-to-smoothness tradeoff along some direction. At the core of this theoretical guarantee on smoothness is an improved lower bound we prove on the optimality gap of the analytic center associated with a convex Lipschitz function, which we believe could be of independent interest. We validate our theoretical findings via experiments, demonstrating the merits of our smoothing approach over randomized smoothing.

On the Hardness of Meaningful Local Guarantees in Nonsmooth Nonconvex Optimization

We study the oracle complexity of nonsmooth nonconvex optimization, with the algorithm assumed to have access only to local function information. It has been shown by Davis, Drusvyatskiy, and Jiang (2023) that for nonsmooth Lipschitz functions satisfying certain regularity and strictness conditions, perturbed gradient descent converges to local minimizers asymptotically. Motivated by this result and by other recent algorithmic advances in nonconvex nonsmooth optimization concerning Goldstein stationarity, we consider the question of obtaining a non-asymptotic rate of convergence to local minima for this problem class. We provide the following negative answer to this question: Local algorithms acting on regular Lipschitz functions cannot, in the worst case, provide meaningful local guarantees in terms of function value in sub-exponential time, even when all near-stationary points are global minima. This sharply contrasts with the smooth setting, for which it is well-known that standard gradient methods can do so in a dimension-independent rate. Our result complements the rich body of work in the theoretical computer science literature that provide hardness results conditional on conjectures such as $\mathsf{P}\neq\mathsf{NP}$ or cryptographic assumptions, in that ours holds unconditional of any such assumptions.

First-Order Methods for Linearly Constrained Bilevel Optimization

Algorithms for bilevel optimization often encounter Hessian computations, which are prohibitive in high dimensions. While recent works offer first-order methods for unconstrained bilevel problems, the constrained setting remains relatively underexplored. We present first-order linearly constrained optimization methods with finite-time hypergradient stationarity guarantees. For linear equality constraints, we attain $\epsilon$-stationarity in $\widetilde{O}(\epsilon^{-2})$ gradient oracle calls, which is nearly-optimal. For linear inequality constraints, we attain $(\delta,\epsilon)$-Goldstein stationarity in $\widetilde{O}(d{\delta^{-1} \epsilon^{-3}})$ gradient oracle calls, where $d$ is the upper-level dimension. Finally, we obtain for the linear inequality setting dimension-free rates of $\widetilde{O}({\delta^{-1} \epsilon^{-4}})$ oracle complexity under the additional assumption of oracle access to the optimal dual variable. Along the way, we develop new nonsmooth nonconvex optimization methods with inexact oracles. We verify these guarantees with preliminary numerical experiments.

Computing Approximate $\ell_p$ Sensitivities

Recent works in dimensionality reduction for regression tasks have introduced the notion of sensitivity, an estimate of the importance of a specific datapoint in a dataset, offering provable guarantees on the quality of the approximation after removing low-sensitivity datapoints via subsampling. However, fast algorithms for approximating $\ell_p$ sensitivities, which we show is equivalent to approximate $\ell_p$ regression, are known for only the $\ell_2$ setting, in which they are termed leverage scores. In this work, we provide efficient algorithms for approximating $\ell_p$ sensitivities and related summary statistics of a given matrix. In particular, for a given $n \times d$ matrix, we compute $\alpha$-approximation to its $\ell_1$ sensitivities at the cost of $O(n/\alpha)$ sensitivity computations. For estimating the total $\ell_p$ sensitivity (i.e. the sum of $\ell_p$ sensitivities), we provide an algorithm based on importance sampling of $\ell_p$ Lewis weights, which computes a constant factor approximation to the total sensitivity at the cost of roughly $O(\sqrt{d})$ sensitivity computations. Furthermore, we estimate the maximum $\ell_1$ sensitivity, up to a $\sqrt{d}$ factor, using $O(d)$ sensitivity computations. We generalize all these results to $\ell_p$ norms for $p > 1$. Lastly, we experimentally show that for a wide class of matrices in real-world datasets, the total sensitivity can be quickly approximated and is significantly smaller than the theoretical prediction, demonstrating that real-world datasets have low intrinsic effective dimensionality.

Online Bidding Algorithms for Return-on-Spend Constrained Advertisers

Online advertising has recently grown into a highly competitive and complex multi-billion-dollar industry, with advertisers bidding for ad slots at large scales and high frequencies. This has resulted in a growing need for efficient "auto-bidding" algorithms that determine the bids for incoming queries to maximize advertisers' targets subject to their specified constraints. This work explores efficient online algorithms for a single value-maximizing advertiser under an increasingly popular constraint: Return-on-Spend (RoS). We quantify efficiency in terms of regret relative to the optimal algorithm, which knows all queries a priori. We contribute a simple online algorithm that achieves near-optimal regret in expectation while always respecting the specified RoS constraint when the input sequence of queries are i.i.d. samples from some distribution. We also integrate our results with the previous work of Balseiro, Lu, and Mirrokni [BLM20] to achieve near-optimal regret while respecting both RoS and fixed budget constraints. Our algorithm follows the primal-dual framework and uses online mirror descent (OMD) for the dual updates. However, we need to use a non-canonical setup of OMD, and therefore the classic low-regret guarantee of OMD, which is for the adversarial setting in online learning, no longer holds. Nonetheless, in our case and more generally where low-regret dynamics are applied in algorithm design, the gradients encountered by OMD can be far from adversarial but influenced by our algorithmic choices. We exploit this key insight to show our OMD setup achieves low regret in the realm of our algorithm.

Decomposable Non-Smooth Convex Optimization with Nearly-Linear Gradient Oracle Complexity

Many fundamental problems in machine learning can be formulated by the convex program \[ \min_{\theta\in R^d}\ \sum_{i=1}^{n}f_{i}(\theta), \] where each $f_i$ is a convex, Lipschitz function supported on a subset of $d_i$ coordinates of $\theta$. One common approach to this problem, exemplified by stochastic gradient descent, involves sampling one $f_i$ term at every iteration to make progress. This approach crucially relies on a notion of uniformity across the $f_i$'s, formally captured by their condition number. In this work, we give an algorithm that minimizes the above convex formulation to $\epsilon$-accuracy in $\widetilde{O}(\sum_{i=1}^n d_i \log (1 /\epsilon))$ gradient computations, with no assumptions on the condition number. The previous best algorithm independent of the condition number is the standard cutting plane method, which requires $O(nd \log (1/\epsilon))$ gradient computations. As a corollary, we improve upon the evaluation oracle complexity for decomposable submodular minimization by Axiotis et al. (ICML 2021). Our main technical contribution is an adaptive procedure to select an $f_i$ term at every iteration via a novel combination of cutting-plane and interior-point methods.

A Fast Scale-Invariant Algorithm for Non-negative Least Squares with Non-negative Data

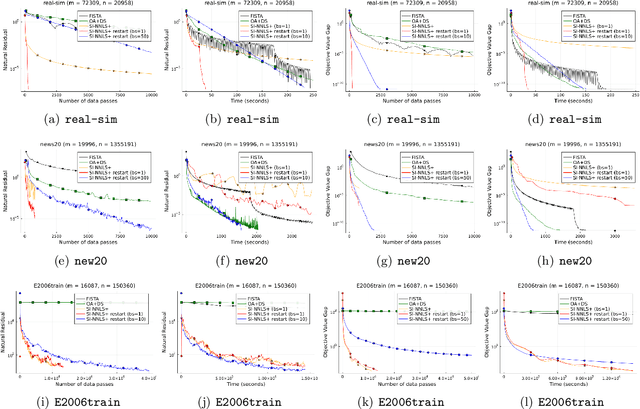
Nonnegative (linear) least square problems are a fundamental class of problems that is well-studied in statistical learning and for which solvers have been implemented in many of the standard programming languages used within the machine learning community. The existing off-the-shelf solvers view the non-negativity constraint in these problems as an obstacle and, compared to unconstrained least squares, perform additional effort to address it. However, in many of the typical applications, the data itself is nonnegative as well, and we show that the nonnegativity in this case makes the problem easier. In particular, while the oracle complexity of unconstrained least squares problems necessarily scales with one of the data matrix constants (typically the spectral norm) and these problems are solved to additive error, we show that nonnegative least squares problems with nonnegative data are solvable to multiplicative error and with complexity that is independent of any matrix constants. The algorithm we introduce is accelerated and based on a primal-dual perspective. We further show how to provably obtain linear convergence using adaptive restart coupled with our method and demonstrate its effectiveness on large-scale data via numerical experiments.