Multi-Armed Bandits with Interference

Experimentation with interference poses a significant challenge in contemporary online platforms. Prior research on experimentation with interference has concentrated on the final output of a policy. The cumulative performance, while equally crucial, is less well understood. To address this gap, we introduce the problem of {\em Multi-armed Bandits with Interference} (MABI), where the learner assigns an arm to each of $N$ experimental units over a time horizon of $T$ rounds. The reward of each unit in each round depends on the treatments of {\em all} units, where the influence of a unit decays in the spatial distance between units. Furthermore, we employ a general setup wherein the reward functions are chosen by an adversary and may vary arbitrarily across rounds and units. We first show that switchback policies achieve an optimal {\em expected} regret $\tilde O(\sqrt T)$ against the best fixed-arm policy. Nonetheless, the regret (as a random variable) for any switchback policy suffers a high variance, as it does not account for $N$. We propose a cluster randomization policy whose regret (i) is optimal in {\em expectation} and (ii) admits a high probability bound that vanishes in $N$.

Faster Rates for Switchback Experiments

Switchback experimental design, wherein a single unit (e.g., a whole system) is exposed to a single random treatment for interspersed blocks of time, tackles both cross-unit and temporal interference. Hu and Wager (2022) recently proposed a treatment-effect estimator that truncates the beginnings of blocks and established a $T^{-1/3}$ rate for estimating the global average treatment effect (GATE) in a Markov setting with rapid mixing. They claim this rate is optimal and suggest focusing instead on a different (and design-dependent) estimand so as to enjoy a faster rate. For the same design we propose an alternative estimator that uses the whole block and surprisingly show that it in fact achieves an estimation rate of $\sqrt{\log T/T}$ for the original design-independent GATE estimand under the same assumptions.

Optimal Decision Tree with Noisy Outcomes

In pool-based active learning, the learner is given an unlabeled data set and aims to efficiently learn the unknown hypothesis by querying the labels of the data points. This can be formulated as the classical Optimal Decision Tree (ODT) problem: Given a set of tests, a set of hypotheses, and an outcome for each pair of test and hypothesis, our objective is to find a low-cost testing procedure (i.e., decision tree) that identifies the true hypothesis. This optimization problem has been extensively studied under the assumption that each test generates a deterministic outcome. However, in numerous applications, for example, clinical trials, the outcomes may be uncertain, which renders the ideas from the deterministic setting invalid. In this work, we study a fundamental variant of the ODT problem in which some test outcomes are noisy, even in the more general case where the noise is persistent, i.e., repeating a test gives the same noisy output. Our approximation algorithms provide guarantees that are nearly best possible and hold for the general case of a large number of noisy outcomes per test or per hypothesis where the performance degrades continuously with this number. We numerically evaluated our algorithms for identifying toxic chemicals and learning linear classifiers, and observed that our algorithms have costs very close to the information-theoretic minimum.

Markdown Pricing Under an Unknown Parametric Demand Model

Consider a single-product revenue-maximization problem where the seller monotonically decreases the price in $n$ rounds with an unknown demand model coming from a given family. Without monotonicity, the minimax regret is $\tilde O(n^{2/3})$ for the Lipschitz demand family and $\tilde O(n^{1/2})$ for a general class of parametric demand models. With monotonicity, the minimax regret is $\tilde O(n^{3/4})$ if the revenue function is Lipschitz and unimodal. However, the minimax regret for parametric families remained open. In this work, we provide a complete settlement for this fundamental problem. We introduce the crossing number to measure the complexity of a family of demand functions. In particular, the family of degree-$k$ polynomials has a crossing number $k$. Based on conservatism under uncertainty, we present (i) a policy with an optimal $\Theta(\log^2 n)$ regret for families with crossing number $k=0$, and (ii) another policy with an optimal $\tilde \Theta(n^{k/(k+1)})$ regret when $k\ge 1$. These bounds are asymptotically higher than the $\tilde O(\log n)$ and $\tilde \Theta(\sqrt n)$ minimax regret for the same families without the monotonicity constraint.

Short-lived High-volume Multi-A/B Testing

Modern platforms leverage randomized experiments to make informed decisions from a given set of items (``treatments''). As a particularly challenging scenario, these items may (i) arrive in high volume, with thousands of new items being released per hour, and (ii) have short lifetime, say, due to the item's transient nature or underlying non-stationarity that impels the platform to perceive the same item as distinct copies over time. Thus motivated, we study a Bayesian multiple-play bandit problem that encapsulates the key features of the multivariate testing (or ``multi-A/B testing'') problem with a high volume of short-lived arms. In each round, a set of $k$ arms arrive, each available for $w$ rounds. Without knowing the mean reward for each arm, the learner selects a multiset of $n$ arms and immediately observes their realized rewards. We aim to minimize the loss due to not knowing the mean rewards, averaged over instances generated from a given prior distribution. We show that when $k = O(n^\rho)$ for some constant $\rho>0$, our proposed policy has $\tilde O(n^{-\min \{\rho, \frac 12 (1+\frac 1w)^{-1}\}})$ loss on a sufficiently large class of prior distributions. We complement this result by showing that every policy suffers $\Omega (n^{-\min \{\rho, \frac 12\}})$ loss on the same class of distributions. We further validate the effectiveness of our policy through a large-scale field experiment on {\em Glance}, a content-card-serving platform that faces exactly the above challenge. A simple variant of our policy outperforms the platform's current recommender by 4.32\% in total duration and 7.48\% in total number of click-throughs.

From Stream to Pool: Dynamic Pricing Beyond i.i.d. Arrivals

The dynamic pricing problem has been extensively studied under the \textbf{stream} model: A stream of customers arrives sequentially, each with an independently and identically distributed valuation. However, this formulation is not entirely reflective of the real world. In many scenarios, high-valuation customers tend to make purchases earlier and leave the market, leading to a \emph{shift} in the valuation distribution. Thus motivated, we consider a model where a \textbf{pool} of $n$ non-strategic unit-demand customers interact repeatedly with the seller. Each customer monitors the price intermittently according to an independent Poisson process and makes a purchase if the observed price is lower than her \emph{private} valuation, whereupon she leaves the market permanently. We present a minimax \emph{optimal} algorithm that efficiently computes a non-adaptive policy which guarantees a $1/k$ fraction of the optimal revenue, given any set of $k$ prices. Moreover, we present an adaptive \emph{learn-then-earn} policy based on a novel \emph{debiasing} approach, and prove an $\tilde O(kn^{3/4})$ regret bound. We further improve the bound to $\tilde O(k^{3/4} n^{3/4})$ using martingale concentration inequalities.

Smooth Non-Stationary Bandits

In many applications of online decision making, the environment is non-stationary and it is therefore crucial to use bandit algorithms that handle changes. Most existing approaches are designed to protect against non-smooth changes, constrained only by total variation or Lipschitzness over time, where they guarantee $T^{2/3}$ regret. However, in practice environments are often changing {\it smoothly}, so such algorithms may incur higher-than-necessary regret in these settings and do not leverage information on the {\it rate of change}. In this paper, we study a non-stationary two-arm bandit problem where we assume an arm's mean reward is a $\beta$-H\"older function over (normalized) time, meaning it is $(\beta-1)$-times Lipschitz-continuously differentiable. We show the first {\it separation} between the smooth and non-smooth regimes by presenting a policy with $T^{3/5}$ regret for $\beta=2$. We complement this result by a $T^{\frac{\beta+1}{2\beta+1}}$ lower bound for any integer $\beta\ge 1$, which matches our upper bound for $\beta=2$.

Approximation Algorithms for Active Sequential Hypothesis Testing

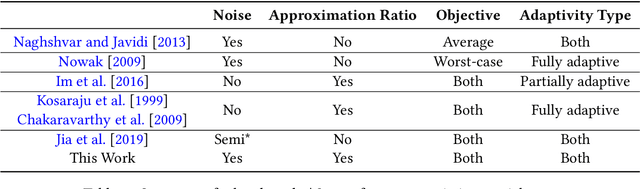
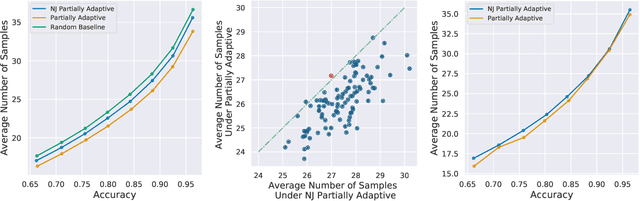
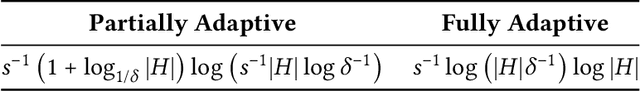
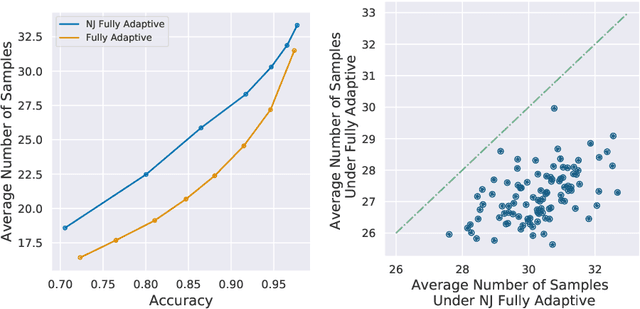
In the problem of active sequential hypotheses testing (ASHT), a learner seeks to identify the true hypothesis $h^*$ from among a set of hypotheses $H$. The learner is given a set of actions and knows the outcome distribution of any action under any true hypothesis. While repeatedly playing the entire set of actions suffices to identify $h^*$, a cost is incurred with each action. Thus, given a target error $\delta>0$, the goal is to find the minimal cost policy for sequentially selecting actions that identify $h^*$ with probability at least $1 - \delta$. This paper provides the first approximation algorithms for ASHT, under two types of adaptivity. First, a policy is partially adaptive if it fixes a sequence of actions in advance and adaptively decides when to terminate and what hypothesis to return. Under partial adaptivity, we provide an $O\big(s^{-1}(1+\log_{1/\delta}|H|)\log (s^{-1}|H| \log |H|)\big)$-approximation algorithm, where $s$ is a natural separation parameter between the hypotheses. Second, a policy is fully adaptive if action selection is allowed to depend on previous outcomes. Under full adaptivity, we provide an $O(s^{-1}\log (|H|/\delta)\log |H|)$-approximation algorithm. We numerically investigate the performance of our algorithms using both synthetic and real-world data, showing that our algorithms outperform a previously proposed heuristic policy.

Input Aggregated Network for Face Video Representation

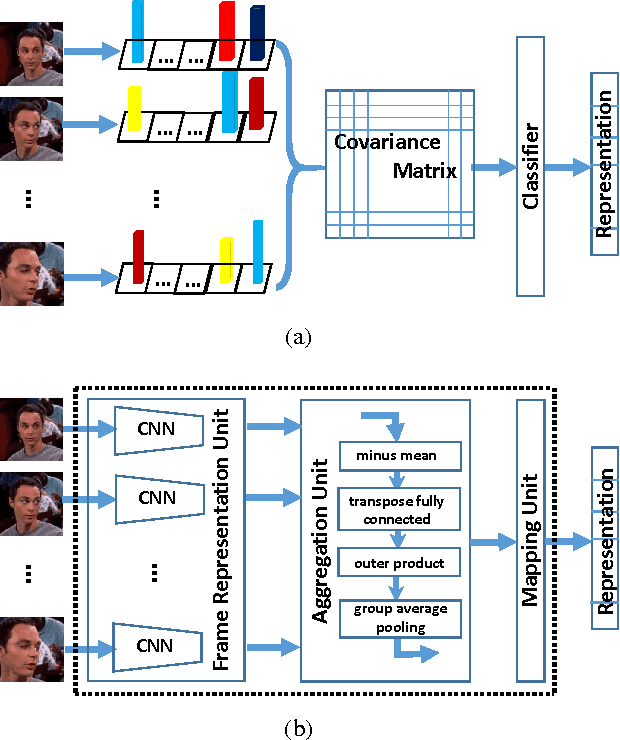
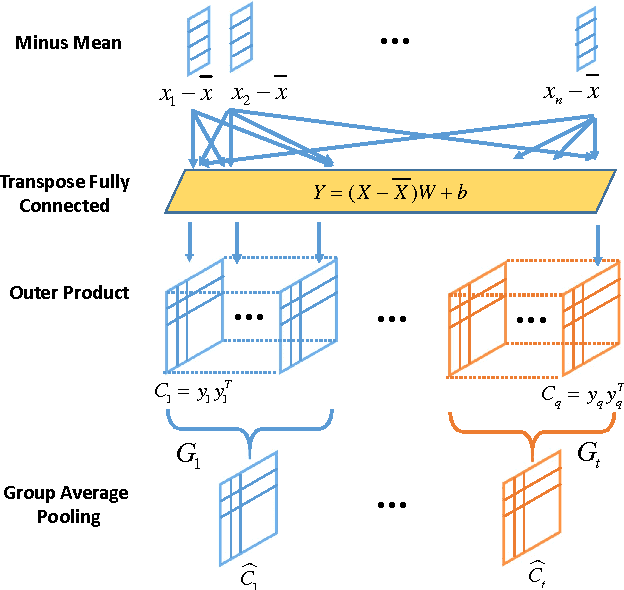
Recently, deep neural network has shown promising performance in face image recognition. The inputs of most networks are face images, and there is hardly any work reported in literature on network with face videos as input. To sufficiently discover the useful information contained in face videos, we present a novel network architecture called input aggregated network which is able to learn fixed-length representations for variable-length face videos. To accomplish this goal, an aggregation unit is designed to model a face video with various frames as a point on a Riemannian manifold, and the mapping unit aims at mapping the point into high-dimensional space where face videos belonging to the same subject are close-by and others are distant. These two units together with the frame representation unit build an end-to-end learning system which can learn representations of face videos for the specific tasks. Experiments on two public face video datasets demonstrate the effectiveness of the proposed network.