Lower Bound on the Greedy Approximation Ratio for Adaptive Submodular Cover

We show that the greedy algorithm for adaptive-submodular cover has approximation ratio at least 1.3*(1+ln Q). Moreover, the instance demonstrating this gap has Q=1. So, it invalidates a prior result in the paper ``Adaptive Submodularity: A New Approach to Active Learning and Stochastic Optimization'' by Golovin-Krause, that claimed a (1+ln Q)^2 approximation ratio for the same algorithm.

Semi-Bandit Learning for Monotone Stochastic Optimization

Stochastic optimization is a widely used approach for optimization under uncertainty, where uncertain input parameters are modeled by random variables. Exact or approximation algorithms have been obtained for several fundamental problems in this area. However, a significant limitation of this approach is that it requires full knowledge of the underlying probability distributions. Can we still get good (approximation) algorithms if these distributions are unknown, and the algorithm needs to learn them through repeated interactions? In this paper, we resolve this question for a large class of "monotone" stochastic problems, by providing a generic online learning algorithm with $\sqrt{T \log T}$ regret relative to the best approximation algorithm (under known distributions). Importantly, our online algorithm works in a semi-bandit setting, where in each period, the algorithm only observes samples from the r.v.s that were actually probed. Our framework applies to several fundamental problems in stochastic optimization such as prophet inequality, Pandora's box, stochastic knapsack, stochastic matchings and stochastic submodular optimization.

Optimal Decision Tree with Noisy Outcomes

In pool-based active learning, the learner is given an unlabeled data set and aims to efficiently learn the unknown hypothesis by querying the labels of the data points. This can be formulated as the classical Optimal Decision Tree (ODT) problem: Given a set of tests, a set of hypotheses, and an outcome for each pair of test and hypothesis, our objective is to find a low-cost testing procedure (i.e., decision tree) that identifies the true hypothesis. This optimization problem has been extensively studied under the assumption that each test generates a deterministic outcome. However, in numerous applications, for example, clinical trials, the outcomes may be uncertain, which renders the ideas from the deterministic setting invalid. In this work, we study a fundamental variant of the ODT problem in which some test outcomes are noisy, even in the more general case where the noise is persistent, i.e., repeating a test gives the same noisy output. Our approximation algorithms provide guarantees that are nearly best possible and hold for the general case of a large number of noisy outcomes per test or per hypothesis where the performance degrades continuously with this number. We numerically evaluated our algorithms for identifying toxic chemicals and learning linear classifiers, and observed that our algorithms have costs very close to the information-theoretic minimum.

An Asymptotically Optimal Batched Algorithm for the Dueling Bandit Problem

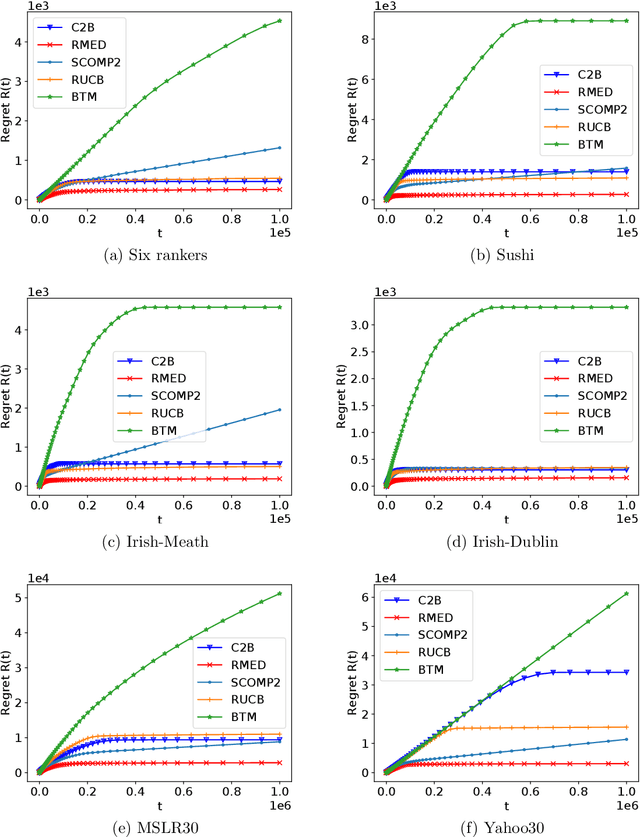
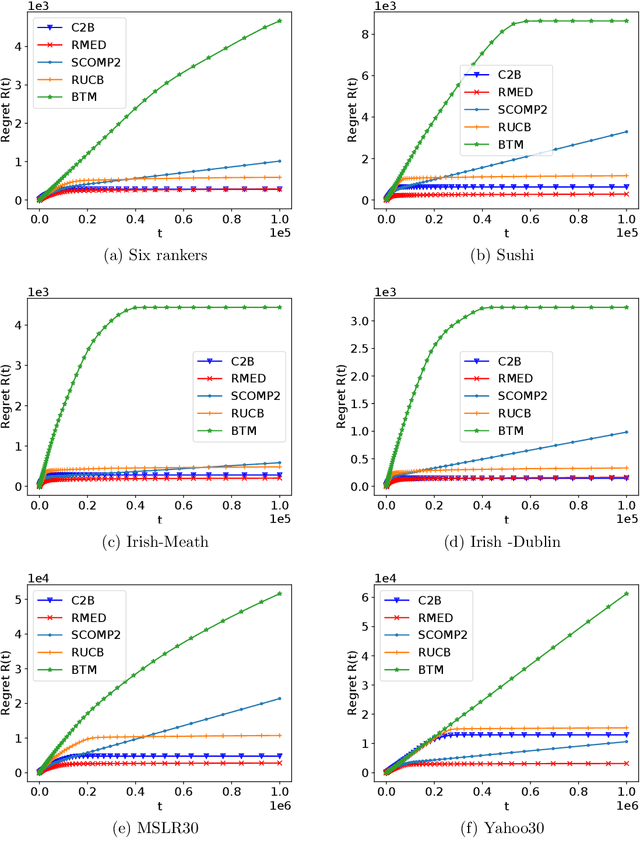
We study the $K$-armed dueling bandit problem, a variation of the traditional multi-armed bandit problem in which feedback is obtained in the form of pairwise comparisons. Previous learning algorithms have focused on the $\textit{fully adaptive}$ setting, where the algorithm can make updates after every comparison. The "batched" dueling bandit problem is motivated by large-scale applications like web search ranking and recommendation systems, where performing sequential updates may be infeasible. In this work, we ask: $\textit{is there a solution using only a few adaptive rounds that matches the asymptotic regret bounds of the best sequential algorithms for $K$-armed dueling bandits?}$ We answer this in the affirmative $\textit{under the Condorcet condition}$, a standard setting of the $K$-armed dueling bandit problem. We obtain asymptotic regret of $O(K^2\log^2(K)) + O(K\log(T))$ in $O(\log(T))$ rounds, where $T$ is the time horizon. Our regret bounds nearly match the best regret bounds known in the fully sequential setting under the Condorcet condition. Finally, in computational experiments over a variety of real-world datasets, we observe that our algorithm using $O(\log(T))$ rounds achieves almost the same performance as fully sequential algorithms (that use $T$ rounds).

Minimum Cost Adaptive Submodular Cover

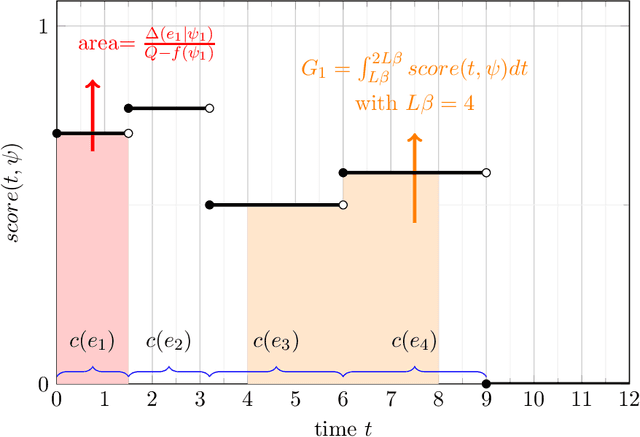
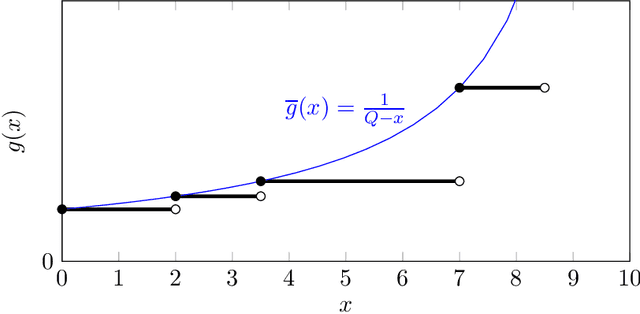
We consider the problem of minimum cost cover of adaptive-submodular functions, and provide a 4(ln Q+1)-approximation algorithm, where Q is the goal value. This bound is nearly the best possible as the problem does not admit any approximation ratio better than ln Q (unless P=NP). Our result is the first O(ln Q)-approximation algorithm for this problem. Previously, O(ln Q) approximation algorithms were only known assuming either independent items or unit-cost items. Furthermore, our result easily extends to the setting where one wants to simultaneously cover multiple adaptive-submodular functions: we obtain the first approximation algorithm for this generalization.

Batched Dueling Bandits

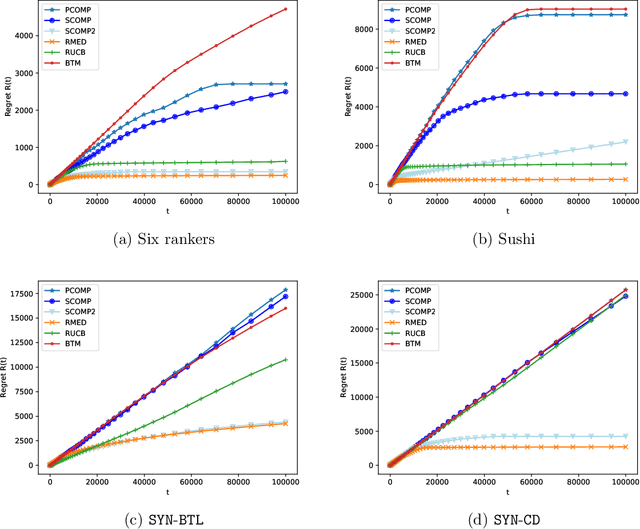
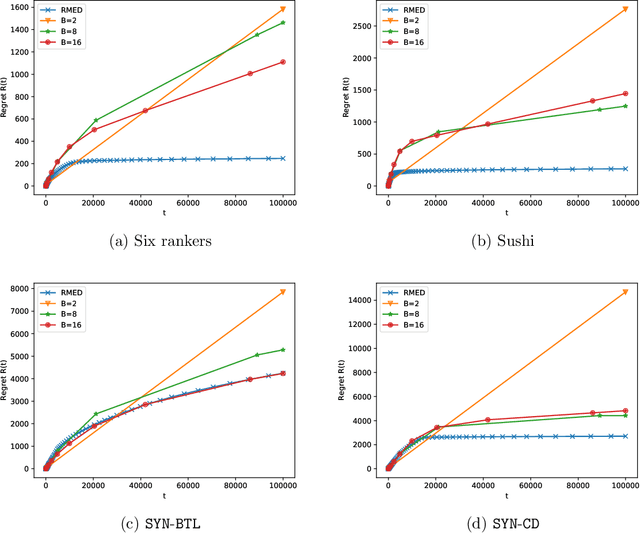
The $K$-armed dueling bandit problem, where the feedback is in the form of noisy pairwise comparisons, has been widely studied. Previous works have only focused on the sequential setting where the policy adapts after every comparison. However, in many applications such as search ranking and recommendation systems, it is preferable to perform comparisons in a limited number of parallel batches. We study the batched $K$-armed dueling bandit problem under two standard settings: (i) existence of a Condorcet winner, and (ii) strong stochastic transitivity and stochastic triangle inequality. For both settings, we obtain algorithms with a smooth trade-off between the number of batches and regret. Our regret bounds match the best known sequential regret bounds (up to poly-logarithmic factors), using only a logarithmic number of batches. We complement our regret analysis with a nearly-matching lower bound. Finally, we also validate our theoretical results via experiments on synthetic and real data.

Adaptive Submodular Ranking

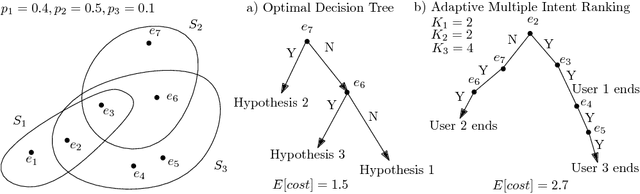
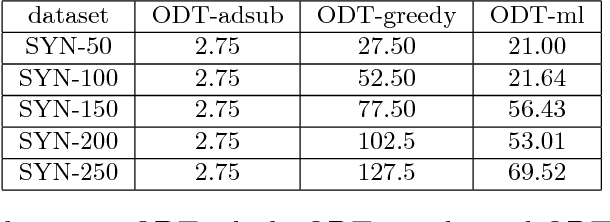
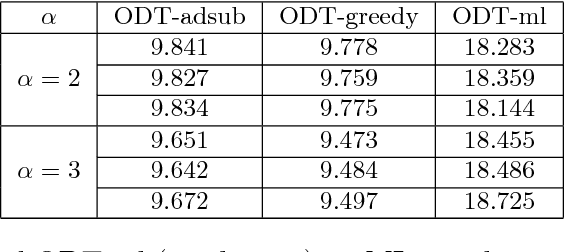
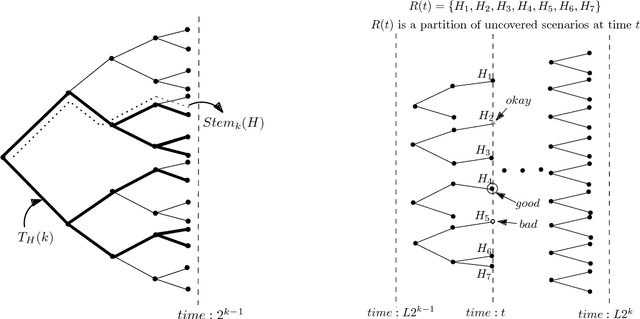
We study a general adaptive ranking problem where an algorithm needs to perform a sequence of actions on a random user, drawn from a known distribution, so as to "satisfy" the user as early as possible. The satisfaction of each user is captured by an individual submodular function, where the user is said to be satisfied when the function value goes above some threshold. We obtain a logarithmic factor approximation algorithm for this adaptive ranking problem, which is the best possible. The adaptive ranking problem has many applications in active learning and ranking: it significantly generalizes previously-studied problems such as optimal decision trees, equivalence class determination, decision region determination and submodular cover. We also present some preliminary experimental results based on our algorithm.