Fatemeh Navidi
Optimal Decision Tree with Noisy Outcomes
Dec 23, 2023



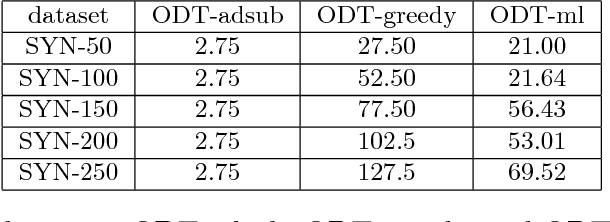
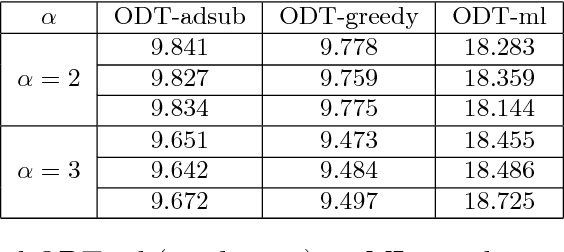
Abstract:In pool-based active learning, the learner is given an unlabeled data set and aims to efficiently learn the unknown hypothesis by querying the labels of the data points. This can be formulated as the classical Optimal Decision Tree (ODT) problem: Given a set of tests, a set of hypotheses, and an outcome for each pair of test and hypothesis, our objective is to find a low-cost testing procedure (i.e., decision tree) that identifies the true hypothesis. This optimization problem has been extensively studied under the assumption that each test generates a deterministic outcome. However, in numerous applications, for example, clinical trials, the outcomes may be uncertain, which renders the ideas from the deterministic setting invalid. In this work, we study a fundamental variant of the ODT problem in which some test outcomes are noisy, even in the more general case where the noise is persistent, i.e., repeating a test gives the same noisy output. Our approximation algorithms provide guarantees that are nearly best possible and hold for the general case of a large number of noisy outcomes per test or per hypothesis where the performance degrades continuously with this number. We numerically evaluated our algorithms for identifying toxic chemicals and learning linear classifiers, and observed that our algorithms have costs very close to the information-theoretic minimum.
Adaptive Submodular Ranking
Jun 05, 2016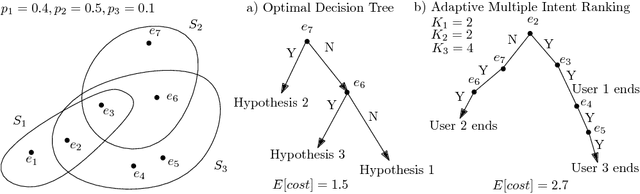
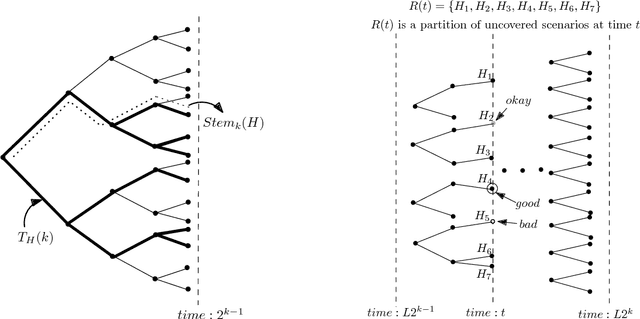
Abstract:We study a general adaptive ranking problem where an algorithm needs to perform a sequence of actions on a random user, drawn from a known distribution, so as to "satisfy" the user as early as possible. The satisfaction of each user is captured by an individual submodular function, where the user is said to be satisfied when the function value goes above some threshold. We obtain a logarithmic factor approximation algorithm for this adaptive ranking problem, which is the best possible. The adaptive ranking problem has many applications in active learning and ranking: it significantly generalizes previously-studied problems such as optimal decision trees, equivalence class determination, decision region determination and submodular cover. We also present some preliminary experimental results based on our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge