Is Flow Matching Just Trajectory Replay for Sequential Data?

Flow matching (FM) is increasingly used for time-series generation, but it is not well understood whether it learns a general dynamical structure or simply performs an effective "trajectory replay". We study this question by deriving the velocity field targeted by the empirical FM objective on sequential data, in the limit of perfect function approximation. For the Gaussian conditional paths commonly used in practice, we show that the implied sampler is an ODE whose dynamics constitutes a nonparametric, memory-augmented continuous-time dynamical system. The optimal field admits a closed-form expression as a similarity-weighted mixture of instantaneous velocities induced by past transitions, making the dataset dependence explicit and interpretable. This perspective positions neural FM models trained by stochastic optimization as parametric surrogates of an ideal nonparametric solution. Using the structure of the optimal field, we study sampling and approximation schemes that improve the efficiency and numerical robustness of ODE-based generation. On nonlinear dynamical system benchmarks, the resulting closed-form sampler yields strong probabilistic forecasts directly from historical transitions, without training.

A Kinetic-Energy Perspective of Flow Matching

Flow-based generative models can be viewed through a physics lens: sampling transports a particle from noise to data by integrating a time-varying velocity field, and each sample corresponds to a trajectory with its own dynamical effort. Motivated by classical mechanics, we introduce Kinetic Path Energy (KPE), an action-like, per-sample diagnostic that measures the accumulated kinetic effort along an Ordinary Differential Equation (ODE) trajectory. Empirically, KPE exhibits two robust correspondences: (i) higher KPE predicts stronger semantic fidelity; (ii) high-KPE trajectories terminate on low-density manifold frontiers. We further provide theoretical guarantees linking trajectory energy to data density. Paradoxically, this correlation is non-monotonic. At sufficiently high energy, generation can degenerate into memorization. Leveraging the closed-form of empirical flow matching, we show that extreme energies drive trajectories toward near-copies of training examples. This yields a Goldilocks principle and motivates Kinetic Trajectory Shaping (KTS), a training-free two-phase inference strategy that boosts early motion and enforces a late-time soft landing, reducing memorization and improving generation quality across benchmark tasks.

On The Hidden Biases of Flow Matching Samplers

We study the implicit bias of flow matching (FM) samplers via the lens of empirical flow matching. Although population FM may produce gradient-field velocities resembling optimal transport (OT), we show that the empirical FM minimizer is almost never a gradient field, even when each conditional flow is. Consequently, empirical FM is intrinsically energetically suboptimal. In view of this, we analyze the kinetic energy of generated samples. With Gaussian sources, both instantaneous and integrated kinetic energies exhibit exponential concentration, while heavy-tailed sources lead to polynomial tails. These behaviors are governed primarily by the choice of source distribution rather than the data. Overall, these notes provide a concise mathematical account of the structural and energetic biases arising in empirical FM.

FLEX: A Backbone for Diffusion-Based Modeling of Spatio-temporal Physical Systems

We introduce FLEX (FLow EXpert), a backbone architecture for generative modeling of spatio-temporal physical systems using diffusion models. FLEX operates in the residual space rather than on raw data, a modeling choice that we motivate theoretically, showing that it reduces the variance of the velocity field in the diffusion model, which helps stabilize training. FLEX integrates a latent Transformer into a U-Net with standard convolutional ResNet layers and incorporates a redesigned skip connection scheme. This hybrid design enables the model to capture both local spatial detail and long-range dependencies in latent space. To improve spatio-temporal conditioning, FLEX uses a task-specific encoder that processes auxiliary inputs such as coarse or past snapshots. Weak conditioning is applied to the shared encoder via skip connections to promote generalization, while strong conditioning is applied to the decoder through both skip and bottleneck features to ensure reconstruction fidelity. FLEX achieves accurate predictions for super-resolution and forecasting tasks using as few as two reverse diffusion steps. It also produces calibrated uncertainty estimates through sampling. Evaluations on high-resolution 2D turbulence data show that FLEX outperforms strong baselines and generalizes to out-of-distribution settings, including unseen Reynolds numbers, physical observables (e.g., fluid flow velocity fields), and boundary conditions.

Elucidating the Design Choice of Probability Paths in Flow Matching for Forecasting

Flow matching has recently emerged as a powerful paradigm for generative modeling and has been extended to probabilistic time series forecasting in latent spaces. However, the impact of the specific choice of probability path model on forecasting performance remains under-explored. In this work, we demonstrate that forecasting spatio-temporal data with flow matching is highly sensitive to the selection of the probability path model. Motivated by this insight, we propose a novel probability path model designed to improve forecasting performance. Our empirical results across various dynamical system benchmarks show that our model achieves faster convergence during training and improved predictive performance compared to existing probability path models. Importantly, our approach is efficient during inference, requiring only a few sampling steps. This makes our proposed model practical for real-world applications and opens new avenues for probabilistic forecasting.

Tuning Frequency Bias of State Space Models

State space models (SSMs) leverage linear, time-invariant (LTI) systems to effectively learn sequences with long-range dependencies. By analyzing the transfer functions of LTI systems, we find that SSMs exhibit an implicit bias toward capturing low-frequency components more effectively than high-frequency ones. This behavior aligns with the broader notion of frequency bias in deep learning model training. We show that the initialization of an SSM assigns it an innate frequency bias and that training the model in a conventional way does not alter this bias. Based on our theory, we propose two mechanisms to tune frequency bias: either by scaling the initialization to tune the inborn frequency bias; or by applying a Sobolev-norm-based filter to adjust the sensitivity of the gradients to high-frequency inputs, which allows us to change the frequency bias via training. Using an image-denoising task, we empirically show that we can strengthen, weaken, or even reverse the frequency bias using both mechanisms. By tuning the frequency bias, we can also improve SSMs' performance on learning long-range sequences, averaging an 88.26% accuracy on the Long-Range Arena (LRA) benchmark tasks.

Gated Recurrent Neural Networks with Weighted Time-Delay Feedback

We introduce a novel gated recurrent unit (GRU) with a weighted time-delay feedback mechanism in order to improve the modeling of long-term dependencies in sequential data. This model is a discretized version of a continuous-time formulation of a recurrent unit, where the dynamics are governed by delay differential equations (DDEs). By considering a suitable time-discretization scheme, we propose $\tau$-GRU, a discrete-time gated recurrent unit with delay. We prove the existence and uniqueness of solutions for the continuous-time model, and we demonstrate that the proposed feedback mechanism can help improve the modeling of long-term dependencies. Our empirical results show that $\tau$-GRU can converge faster and generalize better than state-of-the-art recurrent units and gated recurrent architectures on a range of tasks, including time-series classification, human activity recognition, and speech recognition.

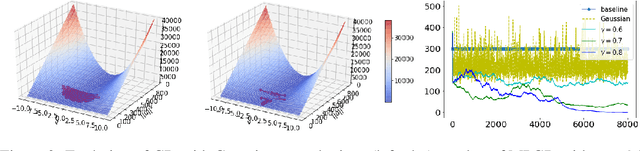
Chaotic Regularization and Heavy-Tailed Limits for Deterministic Gradient Descent

Recent studies have shown that gradient descent (GD) can achieve improved generalization when its dynamics exhibits a chaotic behavior. However, to obtain the desired effect, the step-size should be chosen sufficiently large, a task which is problem dependent and can be difficult in practice. In this study, we incorporate a chaotic component to GD in a controlled manner, and introduce multiscale perturbed GD (MPGD), a novel optimization framework where the GD recursion is augmented with chaotic perturbations that evolve via an independent dynamical system. We analyze MPGD from three different angles: (i) By building up on recent advances in rough paths theory, we show that, under appropriate assumptions, as the step-size decreases, the MPGD recursion converges weakly to a stochastic differential equation (SDE) driven by a heavy-tailed L\'evy-stable process. (ii) By making connections to recently developed generalization bounds for heavy-tailed processes, we derive a generalization bound for the limiting SDE and relate the worst-case generalization error over the trajectories of the process to the parameters of MPGD. (iii) We analyze the implicit regularization effect brought by the dynamical regularization and show that, in the weak perturbation regime, MPGD introduces terms that penalize the Hessian of the loss function. Empirical results are provided to demonstrate the advantages of MPGD.

NoisyMix: Boosting Robustness by Combining Data Augmentations, Stability Training, and Noise Injections

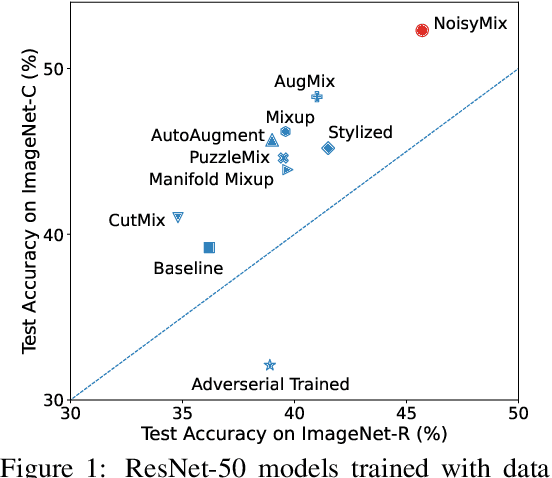
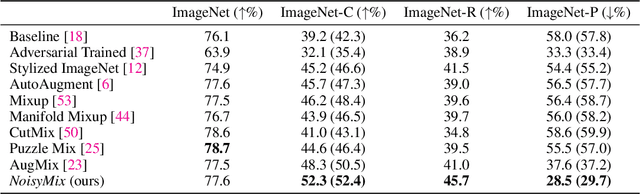
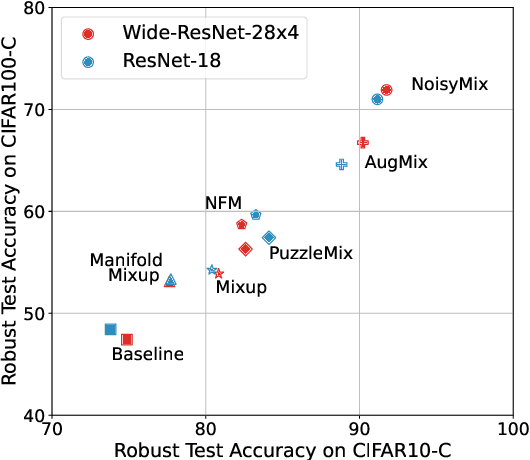
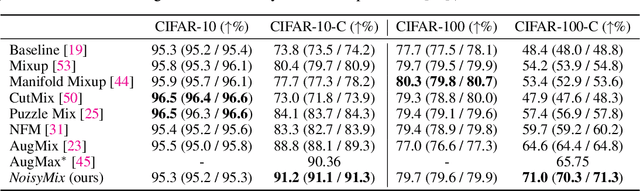
For many real-world applications, obtaining stable and robust statistical performance is more important than simply achieving state-of-the-art predictive test accuracy, and thus robustness of neural networks is an increasingly important topic. Relatedly, data augmentation schemes have been shown to improve robustness with respect to input perturbations and domain shifts. Motivated by this, we introduce NoisyMix, a training scheme that combines data augmentations with stability training and noise injections to improve both model robustness and in-domain accuracy. This combination promotes models that are consistently more robust and that provide well-calibrated estimates of class membership probabilities. We demonstrate the benefits of NoisyMix on a range of benchmark datasets, including ImageNet-C, ImageNet-R, and ImageNet-P. Moreover, we provide theory to understand implicit regularization and robustness of NoisyMix.

Noisy Feature Mixup

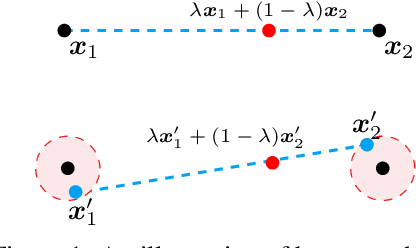
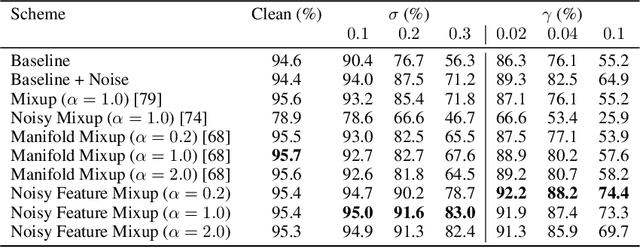
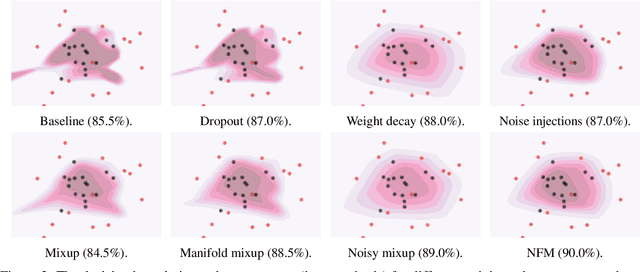
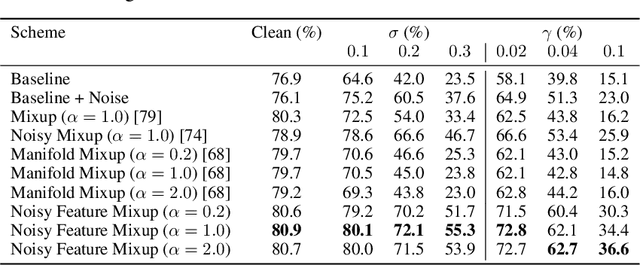
We introduce Noisy Feature Mixup (NFM), an inexpensive yet effective method for data augmentation that combines the best of interpolation based training and noise injection schemes. Rather than training with convex combinations of pairs of examples and their labels, we use noise-perturbed convex combinations of pairs of data points in both input and feature space. This method includes mixup and manifold mixup as special cases, but it has additional advantages, including better smoothing of decision boundaries and enabling improved model robustness. We provide theory to understand this as well as the implicit regularization effects of NFM. Our theory is supported by empirical results, demonstrating the advantage of NFM, as compared to mixup and manifold mixup. We show that residual networks and vision transformers trained with NFM have favorable trade-offs between predictive accuracy on clean data and robustness with respect to various types of data perturbation across a range of computer vision benchmark datasets.