UPETrack: Unidirectional Position Estimation for Tracking Occluded Deformable Linear Objects

Real-time state tracking of Deformable Linear Objects (DLOs) is critical for enabling robotic manipulation of DLOs in industrial assembly, medical procedures, and daily-life applications. However, the high-dimensional configuration space, nonlinear dynamics, and frequent partial occlusions present fundamental barriers to robust real-time DLO tracking. To address these limitations, this study introduces UPETrack, a geometry-driven framework based on Unidirectional Position Estimation (UPE), which facilitates tracking without the requirement for physical modeling, virtual simulation, or visual markers. The framework operates in two phases: (1) visible segment tracking is based on a Gaussian Mixture Model (GMM) fitted via the Expectation Maximization (EM) algorithm, and (2) occlusion region prediction employing UPE algorithm we proposed. UPE leverages the geometric continuity inherent in DLO shapes and their temporal evolution patterns to derive a closed-form positional estimator through three principal mechanisms: (i) local linear combination displacement term, (ii) proximal linear constraint term, and (iii) historical curvature term. This analytical formulation allows efficient and stable estimation of occluded nodes through explicit linear combinations of geometric components, eliminating the need for additional iterative optimization. Experimental results demonstrate that UPETrack surpasses two state-of-the-art tracking algorithms, including TrackDLO and CDCPD2, in both positioning accuracy and computational efficiency.

Recall and Learn: A Memory-augmented Solver for Math Word Problems

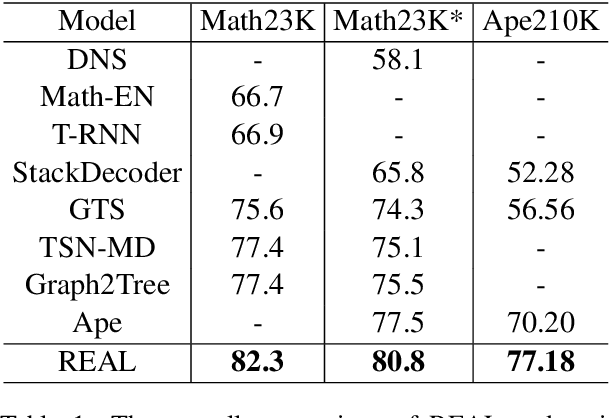
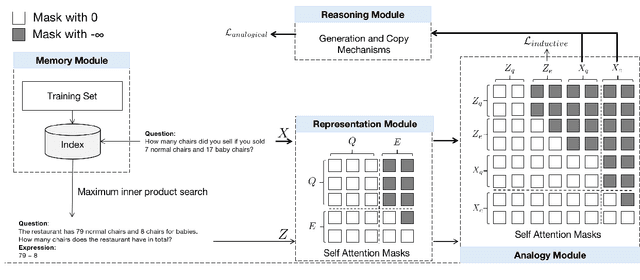
In this article, we tackle the math word problem, namely, automatically answering a mathematical problem according to its textual description. Although recent methods have demonstrated their promising results, most of these methods are based on template-based generation scheme which results in limited generalization capability. To this end, we propose a novel human-like analogical learning method in a recall and learn manner. Our proposed framework is composed of modules of memory, representation, analogy, and reasoning, which are designed to make a new exercise by referring to the exercises learned in the past. Specifically, given a math word problem, the model first retrieves similar questions by a memory module and then encodes the unsolved problem and each retrieved question using a representation module. Moreover, to solve the problem in a way of analogy, an analogy module and a reasoning module with a copy mechanism are proposed to model the interrelationship between the problem and each retrieved question. Extensive experiments on two well-known datasets show the superiority of our proposed algorithm as compared to other state-of-the-art competitors from both overall performance comparison and micro-scope studies.