Unrolling Particles: Unsupervised Learning of Sampling Distributions

Particle filtering is used to compute good nonlinear estimates of complex systems. It samples trajectories from a chosen distribution and computes the estimate as a weighted average. Easy-to-sample distributions often lead to degenerate samples where only one trajectory carries all the weight, negatively affecting the resulting performance of the estimate. While much research has been done on the design of appropriate sampling distributions that would lead to controlled degeneracy, in this paper our objective is to \emph{learn} sampling distributions. Leveraging the framework of algorithm unrolling, we model the sampling distribution as a multivariate normal, and we use neural networks to learn both the mean and the covariance. We carry out unsupervised training of the model to minimize weight degeneracy, relying only on the observed measurements of the system. We show in simulations that the resulting particle filter yields good estimates in a wide range of scenarios.

Joint inference of multiple graphs with hidden variables from stationary graph signals

Learning graphs from sets of nodal observations represents a prominent problem formally known as graph topology inference. However, current approaches are limited by typically focusing on inferring single networks, and they assume that observations from all nodes are available. First, many contemporary setups involve multiple related networks, and second, it is often the case that only a subset of nodes is observed while the rest remain hidden. Motivated by these facts, we introduce a joint graph topology inference method that models the influence of the hidden variables. Under the assumptions that the observed signals are stationary on the sought graphs and the graphs are closely related, the joint estimation of multiple networks allows us to exploit such relationships to improve the quality of the learned graphs. Moreover, we confront the challenging problem of modeling the influence of the hidden nodes to minimize their detrimental effect. To obtain an amenable approach, we take advantage of the particular structure of the setup at hand and leverage the similarity between the different graphs, which affects both the observed and the hidden nodes. To test the proposed method, numerical simulations over synthetic and real-world graphs are provided.

A Robust Alternative for Graph Convolutional Neural Networks via Graph Neighborhood Filters

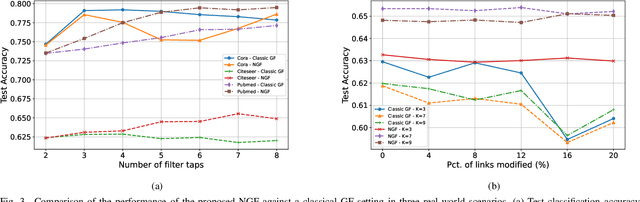
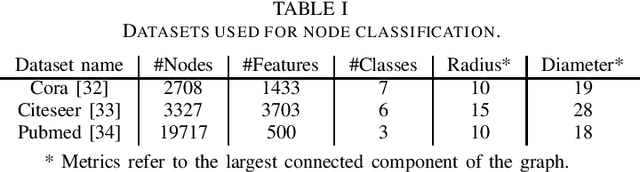
Graph convolutional neural networks (GCNNs) are popular deep learning architectures that, upon replacing regular convolutions with graph filters (GFs), generalize CNNs to irregular domains. However, classical GFs are prone to numerical errors since they consist of high-order polynomials. This problem is aggravated when several filters are applied in cascade, limiting the practical depth of GCNNs. To tackle this issue, we present the neighborhood graph filters (NGFs), a family of GFs that replaces the powers of the graph shift operator with $k$-hop neighborhood adjacency matrices. NGFs help to alleviate the numerical issues of traditional GFs, allow for the design of deeper GCNNs, and enhance the robustness to errors in the topology of the graph. To illustrate the advantage over traditional GFs in practical applications, we use NGFs in the design of deep neighborhood GCNNs to solve graph signal denoising and node classification problems over both synthetic and real-world data.

Untrained Graph Neural Networks for Denoising

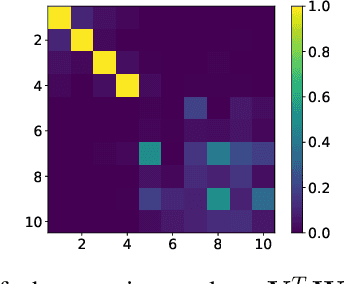
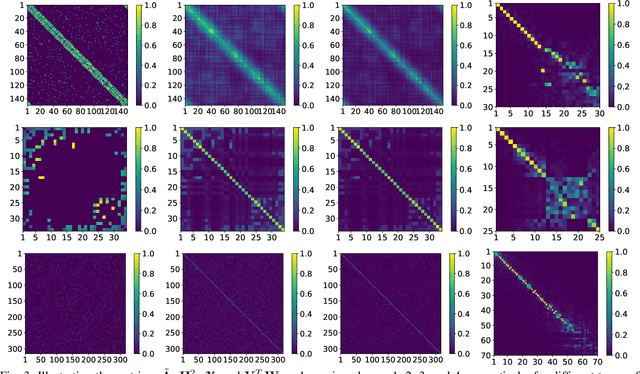
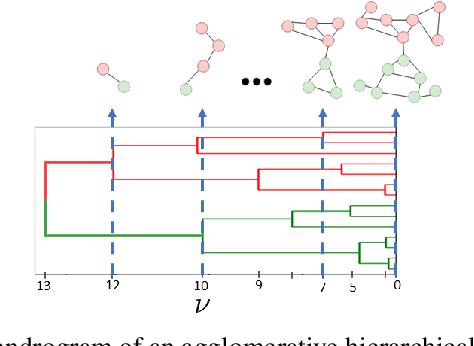
A fundamental problem in signal processing is to denoise a signal. While there are many well-performing methods for denoising signals defined on regular supports, such as images defined on two-dimensional grids of pixels, many important classes of signals are defined over irregular domains such as graphs. This paper introduces two untrained graph neural network architectures for graph signal denoising, provides theoretical guarantees for their denoising capabilities in a simple setup, and numerically validates the theoretical results in more general scenarios. The two architectures differ on how they incorporate the information encoded in the graph, with one relying on graph convolutions and the other employing graph upsampling operators based on hierarchical clustering. Each architecture implements a different prior over the targeted signals. To numerically illustrate the validity of the theoretical results and to compare the performance of the proposed architectures with other denoising alternatives, we present several experimental results with real and synthetic datasets.

Hodgelets: Localized Spectral Representations of Flows on Simplicial Complexes

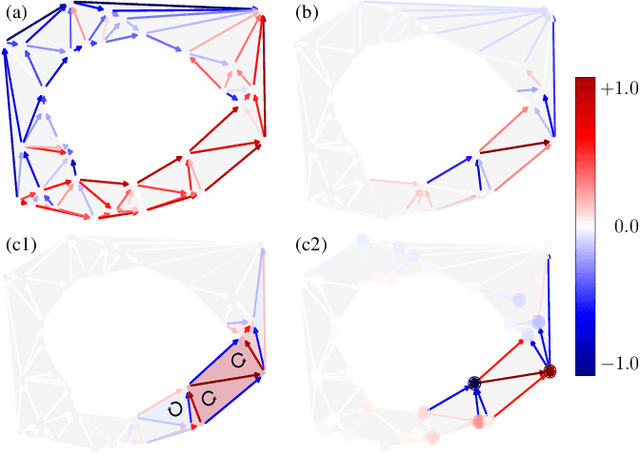
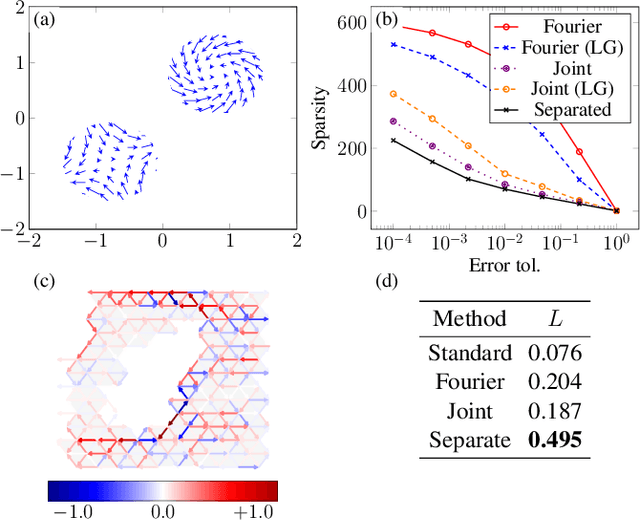
We develop wavelet representations for edge-flows on simplicial complexes, using ideas rooted in combinatorial Hodge theory and spectral graph wavelets. We first show that the Hodge Laplacian can be used in lieu of the graph Laplacian to construct a family of wavelets for higher-order signals on simplicial complexes. Then, we refine this idea to construct wavelets that respect the Hodge-Helmholtz decomposition. For these Hodgelets, familiar notions of curl-free and divergence-free flows from vector calculus are preserved. We characterize the representational quality of our Hodgelets for edge flows in terms of frame bounds and demonstrate the use of these spectral wavelets for sparse representation of edge flows on real and synthetic data.

ML-aided power allocation for Tactical MIMO

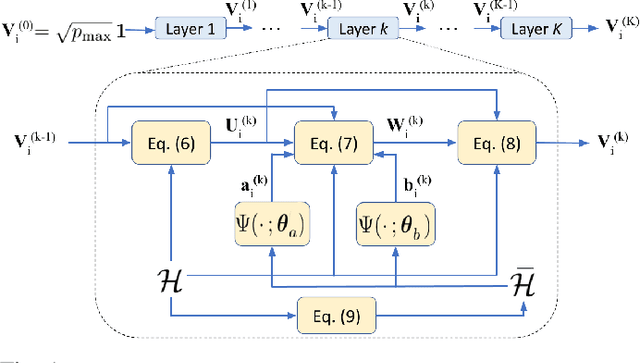
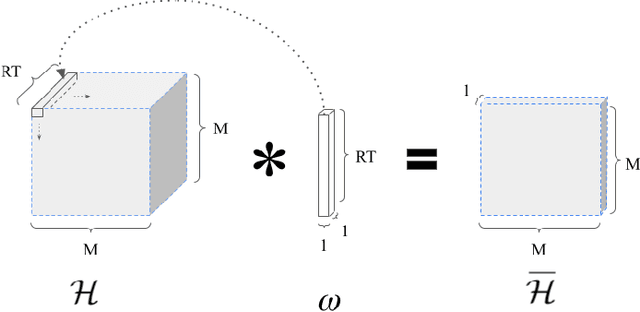
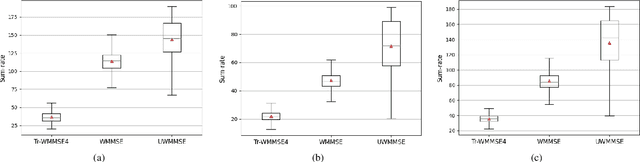
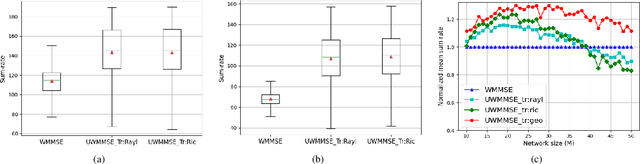
We study the problem of optimal power allocation in single-hop multi-antenna ad-hoc wireless networks. A standard technique to solve this problem involves optimizing a tri-convex function under power constraints using a block-coordinate-descent (BCD) based iterative algorithm. This approach, termed WMMSE, tends to be computationally complex and time consuming. Several learning-based approaches have been proposed to speed up the power allocation process. A recent work, UWMMSE, learns an affine transformation of a WMMSE parameter in an unfolded structure to accelerate convergence. In spite of achieving promising results, its application is limited to single-antenna wireless networks. In this work, we present a UWMMSE framework for power allocation in (multiple-input multiple-output) MIMO interference networks. Through an empirical study, we illustrate the superiority of our approach in comparison to WMMSE and also analyze its robustness to changes in channel conditions and network size.

Link Scheduling using Graph Neural Networks

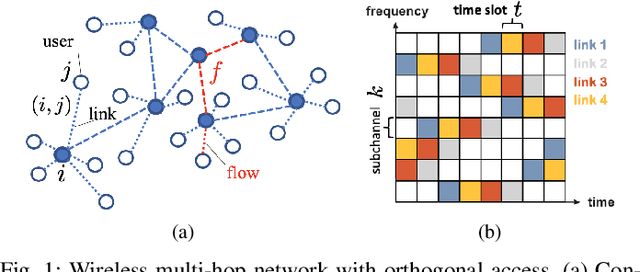
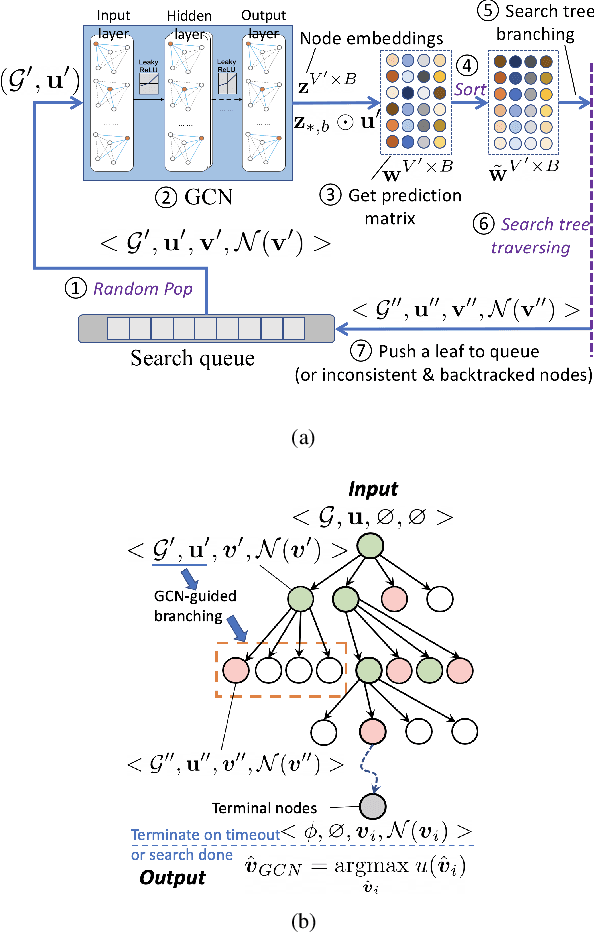
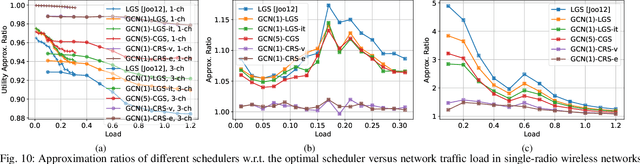
Efficient scheduling of transmissions is a key problem in wireless networks. The main challenge stems from the fact that optimal link scheduling involves solving a maximum weighted independent set (MWIS) problem, which is known to be NP-hard. For practical link scheduling schemes, centralized and distributed greedy heuristics are commonly used to approximate the solution to the MWIS problem. However, these greedy schemes mostly ignore important topological information of the wireless network. To overcome this limitation, we propose fast heuristics based on graph convolutional networks (GCNs) that can be implemented in centralized and distributed manners. Our centralized MWIS solver is based on tree search guided by a trainable GCN module and 1-step rollout. In our distributed MWIS solver, a trainable GCN module learns topology-aware node embeddings that are combined with the network weights before calling a distributed greedy solver. Test results on medium-sized wireless networks show that a GCN-based centralized MWIS solver can reach a near-optimal solution quickly. Moreover, we demonstrate that a shallow GCN-based distributed MWIS scheduler can reduce by nearly half the suboptimality gap of the distributed greedy solver with minimal increase in complexity. The proposed scheduling solutions also exhibit good generalizability across graph and weight distributions.

Robust Hierarchical Clustering for Directed Networks: An Axiomatic Approach

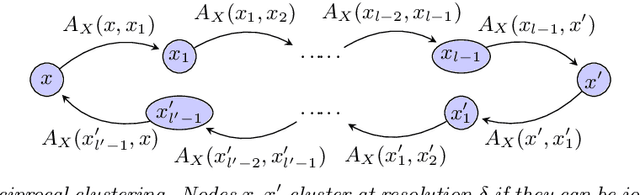
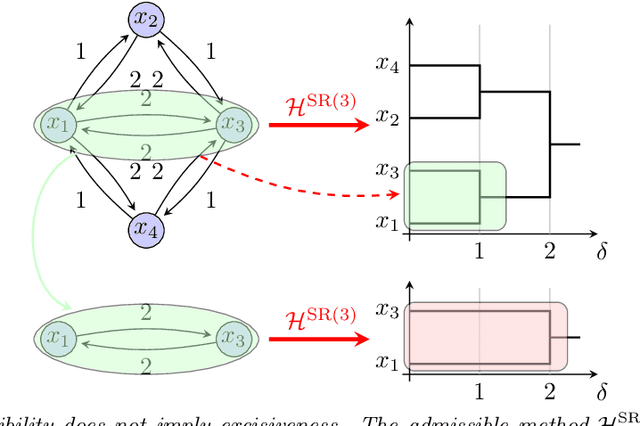
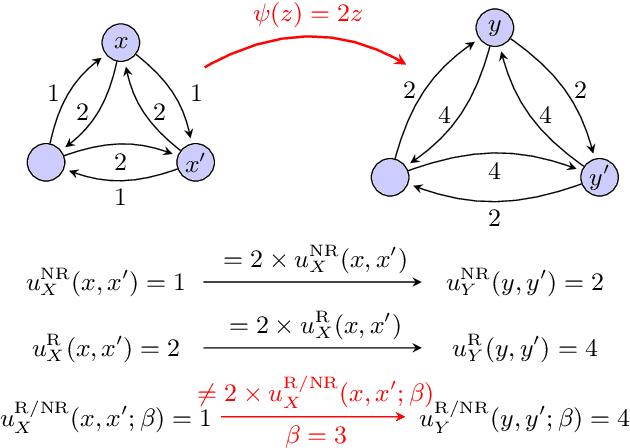
We provide a complete taxonomic characterization of robust hierarchical clustering methods for directed networks following an axiomatic approach. We begin by introducing three practical properties associated with the notion of robustness in hierarchical clustering: linear scale preservation, stability, and excisiveness. Linear scale preservation enforces imperviousness to change in units of measure whereas stability ensures that a bounded perturbation in the input network entails a bounded perturbation in the clustering output. Excisiveness refers to the local consistency of the clustering outcome. Algorithmically, excisiveness implies that we can reduce computational complexity by only clustering a subset of our data while theoretically guaranteeing that the same hierarchical outcome would be observed when clustering the whole dataset. In parallel to these three properties, we introduce the concept of representability, a generative model for describing clustering methods through the specification of their action on a collection of networks. Our main result is to leverage this generative model to give a precise characterization of all robust -- i.e., excisive, linear scale preserving, and stable -- hierarchical clustering methods for directed networks. We also address the implementation of our methods and describe an application to real data.

Signal processing on simplicial complexes

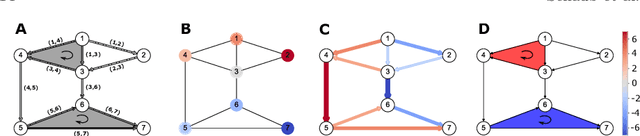
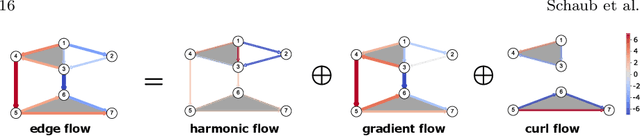
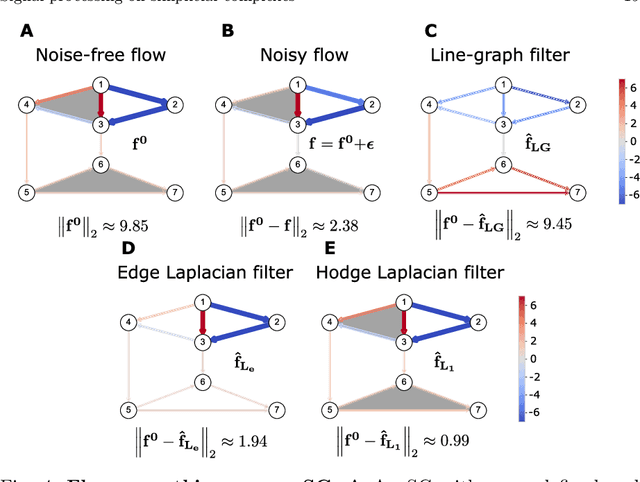
Higher-order networks have so far been considered primarily in the context of studying the structure of complex systems, i.e., the higher-order or multi-way relations connecting the constituent entities. More recently, a number of studies have considered dynamical processes that explicitly account for such higher-order dependencies, e.g., in the context of epidemic spreading processes or opinion formation. In this chapter, we focus on a closely related, but distinct third perspective: how can we use higher-order relationships to process signals and data supported on higher-order network structures. In particular, we survey how ideas from signal processing of data supported on regular domains, such as time series or images, can be extended to graphs and simplicial complexes. We discuss Fourier analysis, signal denoising, signal interpolation, and nonlinear processing through neural networks based on simplicial complexes. Key to our developments is the Hodge Laplacian matrix, a multi-relational operator that leverages the special structure of simplicial complexes and generalizes desirable properties of the Laplacian matrix in graph signal processing.

Graph-signal Reconstruction and Blind Deconvolution for Structured Inputs

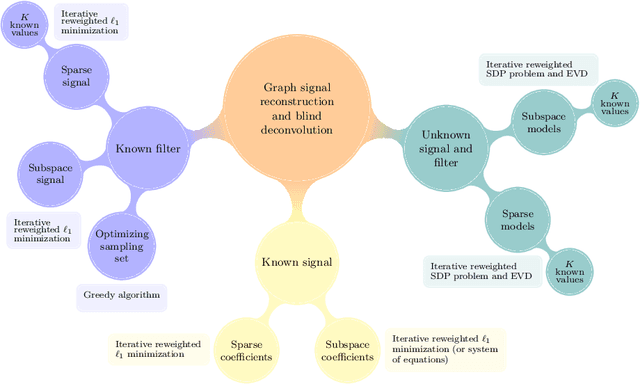
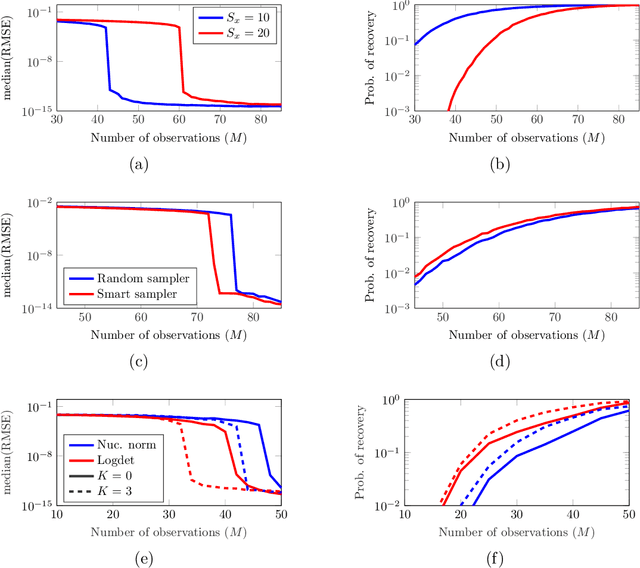
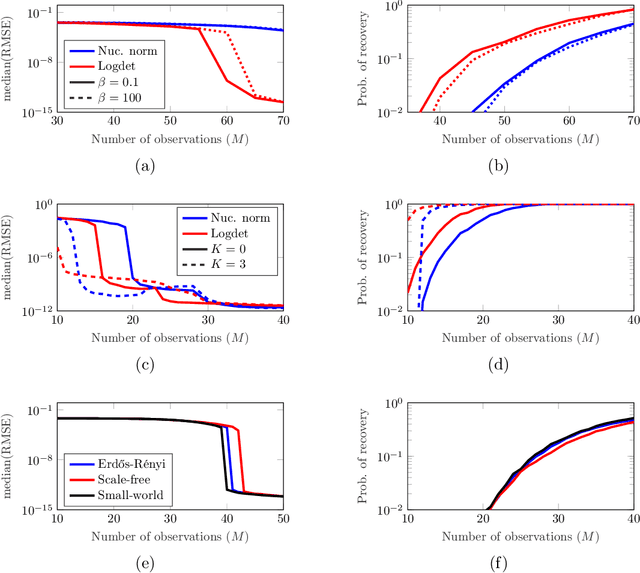
Key to successfully deal with complex contemporary datasets is the development of tractable models that account for the irregular structure of the information at hand. This paper provides a comprehensive and unifying view of several sampling, reconstruction, and recovery problems for signals defined on irregular domains that can be accurately represented by a graph. The workhorse assumption is that the (partially) observed signals can be modeled as the output of a graph filter to a structured (parsimonious) input graph signal. When either the input or the filter coefficients are known, this is tantamount to assuming that the signals of interest live on a subspace defined by the supporting graph. When neither is known, the model becomes bilinear. Upon imposing different priors and additional structure on either the input or the filter coefficients, a broad range of relevant problem formulations arise. The goal is then to leverage those priors, the shift operator of the supporting graph, and the samples of the signal of interest to recover: the signal at the non-sampled nodes (graph-signal interpolation), the input (deconvolution), the filter coefficients (system identification), or any combination thereof (blind deconvolution).