Model-Driven Graph Contrastive Learning

We propose $\textbf{MGCL}$, a model-driven graph contrastive learning (GCL) framework that leverages graphons (probabilistic generative models for graphs) to guide contrastive learning by accounting for the data's underlying generative process. GCL has emerged as a powerful self-supervised framework for learning expressive node or graph representations without relying on annotated labels, which are often scarce in real-world data. By contrasting augmented views of graph data, GCL has demonstrated strong performance across various downstream tasks, such as node and graph classification. However, existing methods typically rely on manually designed or heuristic augmentation strategies that are not tailored to the underlying data distribution and operate at the individual graph level, ignoring similarities among graphs generated from the same model. Conversely, in our proposed approach, MGCL first estimates the graphon associated with the observed data and then defines a graphon-informed augmentation process, enabling data-adaptive and principled augmentations. Additionally, for graph-level tasks, MGCL clusters the dataset and estimates a graphon per group, enabling contrastive pairs to reflect shared semantics and structure. Extensive experiments on benchmark datasets demonstrate that MGCL achieves state-of-the-art performance, highlighting the advantages of incorporating generative models into GCL.

Graph Guided Diffusion: Unified Guidance for Conditional Graph Generation

Diffusion models have emerged as powerful generative models for graph generation, yet their use for conditional graph generation remains a fundamental challenge. In particular, guiding diffusion models on graphs under arbitrary reward signals is difficult: gradient-based methods, while powerful, are often unsuitable due to the discrete and combinatorial nature of graphs, and non-differentiable rewards further complicate gradient-based guidance. We propose Graph Guided Diffusion (GGDiff), a novel guidance framework that interprets conditional diffusion on graphs as a stochastic control problem to address this challenge. GGDiff unifies multiple guidance strategies, including gradient-based guidance (for differentiable rewards), control-based guidance (using control signals from forward reward evaluations), and zero-order approximations (bridging gradient-based and gradient-free optimization). This comprehensive, plug-and-play framework enables zero-shot guidance of pre-trained diffusion models under both differentiable and non-differentiable reward functions, adapting well-established guidance techniques to graph generation--a direction largely unexplored. Our formulation balances computational efficiency, reward alignment, and sample quality, enabling practical conditional generation across diverse reward types. We demonstrate the efficacy of GGDiff in various tasks, including constraints on graph motifs, fairness, and link prediction, achieving superior alignment with target rewards while maintaining diversity and fidelity.

Scalable Implicit Graphon Learning

Graphons are continuous models that represent the structure of graphs and allow the generation of graphs of varying sizes. We propose Scalable Implicit Graphon Learning (SIGL), a scalable method that combines implicit neural representations (INRs) and graph neural networks (GNNs) to estimate a graphon from observed graphs. Unlike existing methods, which face important limitations like fixed resolution and scalability issues, SIGL learns a continuous graphon at arbitrary resolutions. GNNs are used to determine the correct node ordering, improving graph alignment. Furthermore, we characterize the asymptotic consistency of our estimator, showing that more expressive INRs and GNNs lead to consistent estimators. We evaluate SIGL in synthetic and real-world graphs, showing that it outperforms existing methods and scales effectively to larger graphs, making it ideal for tasks like graph data augmentation.

Repulsive Score Distillation for Diverse Sampling of Diffusion Models

Score distillation sampling has been pivotal for integrating diffusion models into generation of complex visuals. Despite impressive results it suffers from mode collapse and lack of diversity. To cope with this challenge, we leverage the gradient flow interpretation of score distillation to propose Repulsive Score Distillation (RSD). In particular, we propose a variational framework based on repulsion of an ensemble of particles that promotes diversity. Using a variational approximation that incorporates a coupling among particles, the repulsion appears as a simple regularization that allows interaction of particles based on their relative pairwise similarity, measured e.g., via radial basis kernels. We design RSD for both unconstrained and constrained sampling scenarios. For constrained sampling we focus on inverse problems in the latent space that leads to an augmented variational formulation, that strikes a good balance between compute, quality and diversity. Our extensive experiments for text-to-image generation, and inverse problems demonstrate that RSD achieves a superior trade-off between diversity and quality compared with state-of-the-art alternatives.

Joint channel estimation and data detection in massive MIMO systems based on diffusion models

We propose a joint channel estimation and data detection algorithm for massive multilple-input multiple-output systems based on diffusion models. Our proposed method solves the blind inverse problem by sampling from the joint posterior distribution of the symbols and channels and computing an approximate maximum a posteriori estimation. To achieve this, we construct a diffusion process that models the joint distribution of the channels and symbols given noisy observations, and then run the reverse process to generate the samples. A unique contribution of the algorithm is to include the discrete prior distribution of the symbols and a learned prior for the channels. Indeed, this is key as it allows a more efficient exploration of the joint search space and, therefore, enhances the sampling process. Through numerical experiments, we demonstrate that our method yields a lower normalized mean squared error than competing approaches and reduces the pilot overhead.

Solving Linear Inverse Problems using Higher-Order Annealed Langevin Diffusion

We propose a solution for linear inverse problems based on higher-order Langevin diffusion. More precisely, we propose pre-conditioned second-order and third-order Langevin dynamics that provably sample from the posterior distribution of our unknown variables of interest while being computationally more efficient than their first-order counterpart and the non-conditioned versions of both dynamics. Moreover, we prove that both pre-conditioned dynamics are well-defined and have the same unique invariant distributions as the non-conditioned cases. We also incorporate an annealing procedure that has the double benefit of further accelerating the convergence of the algorithm and allowing us to accommodate the case where the unknown variables are discrete. Numerical experiments in two different tasks (MIMO symbol detection and channel estimation) showcase the generality of our method and illustrate the high performance achieved relative to competing approaches (including learning-based ones) while having comparable or lower computational complexity.

Unsupervised Learning of Sampling Distributions for Particle Filters

Accurate estimation of the states of a nonlinear dynamical system is crucial for their design, synthesis, and analysis. Particle filters are estimators constructed by simulating trajectories from a sampling distribution and averaging them based on their importance weight. For particle filters to be computationally tractable, it must be feasible to simulate the trajectories by drawing from the sampling distribution. Simultaneously, these trajectories need to reflect the reality of the nonlinear dynamical system so that the resulting estimators are accurate. Thus, the crux of particle filters lies in designing sampling distributions that are both easy to sample from and lead to accurate estimators. In this work, we propose to learn the sampling distributions. We put forward four methods for learning sampling distributions from observed measurements. Three of the methods are parametric methods in which we learn the mean and covariance matrix of a multivariate Gaussian distribution; each methods exploits a different aspect of the data (generic, time structure, graph structure). The fourth method is a nonparametric alternative in which we directly learn a transform of a uniform random variable. All four methods are trained in an unsupervised manner by maximizing the likelihood that the states may have produced the observed measurements. Our computational experiments demonstrate that learned sampling distributions exhibit better performance than designed, minimum-degeneracy sampling distributions.

Accelerated massive MIMO detector based on annealed underdamped Langevin dynamics

We propose a multiple-input multiple-output (MIMO) detector based on an annealed version of the \emph{underdamped} Langevin (stochastic) dynamic. Our detector achieves state-of-the-art performance in terms of symbol error rate (SER) while keeping the computational complexity in check. Indeed, our method can be easily tuned to strike the right balance between computational complexity and performance as required by the application at hand. This balance is achieved by tuning hyperparameters that control the length of the simulated Langevin dynamic. Through numerical experiments, we demonstrate that our detector yields lower SER than competing approaches (including learning-based ones) with a lower running time compared to a previously proposed \emph{overdamped} Langevin-based MIMO detector.

Annealed Langevin Dynamics for Massive MIMO Detection

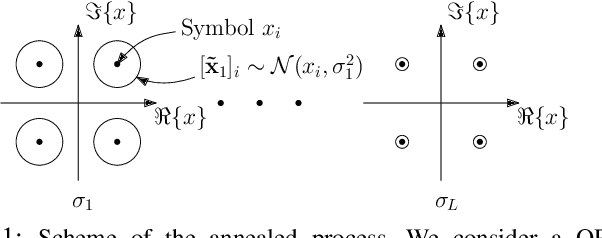
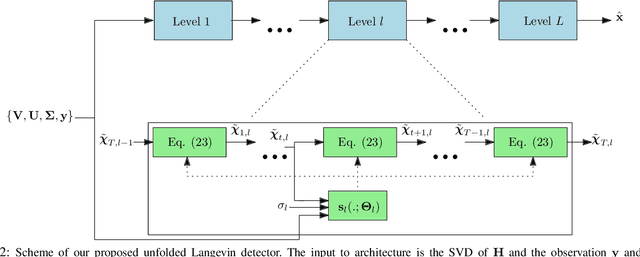
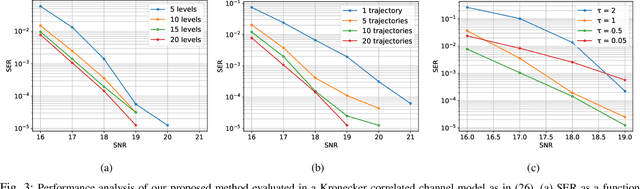
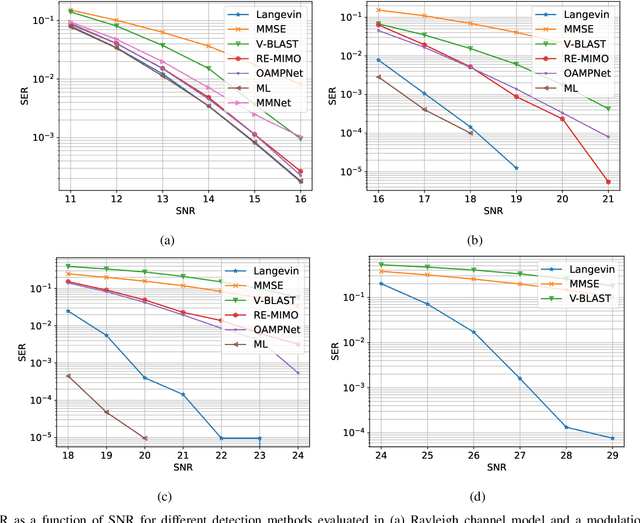
Solving the optimal symbol detection problem in multiple-input multiple-output (MIMO) systems is known to be NP-hard. Hence, the objective of any detector of practical relevance is to get reasonably close to the optimal solution while keeping the computational complexity in check. In this work, we propose a MIMO detector based on an annealed version of Langevin (stochastic) dynamics. More precisely, we define a stochastic dynamical process whose stationary distribution coincides with the posterior distribution of the symbols given our observations. In essence, this allows us to approximate the maximum a posteriori estimator of the transmitted symbols by sampling from the proposed Langevin dynamic. Furthermore, we carefully craft this stochastic dynamic by gradually adding a sequence of noise with decreasing variance to the trajectories, which ensures that the estimated symbols belong to a pre-specified discrete constellation. Based on the proposed MIMO detector, we also design a robust version of the method by unfolding and parameterizing one term -- the score of the likelihood -- by a neural network. Through numerical experiments in both synthetic and real-world data, we show that our proposed detector yields state-of-the-art symbol error rate performance and the robust version becomes noise-variance agnostic.

Detection by Sampling: Massive MIMO Detector based on Langevin Dynamics

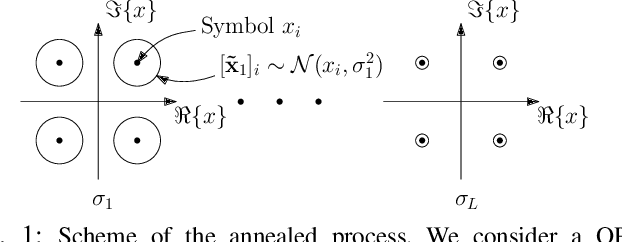
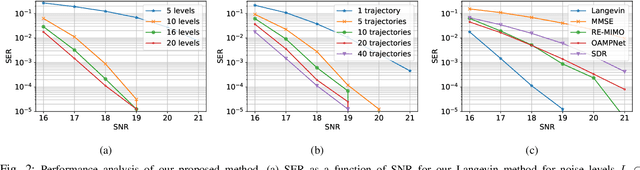
Optimal symbol detection in multiple-input multiple-output (MIMO) systems is known to be an NP-hard problem. Hence, the objective of any detector of practical relevance is to get reasonably close to the optimal solution while keeping the computational complexity in check. In this work, we propose a MIMO detector based on an annealed version of Langevin (stochastic) dynamics. More precisely, we define a stochastic dynamical process whose stationary distribution coincides with the posterior distribution of the symbols given our observations. In essence, this allows us to approximate the maximum a posteriori estimator of the transmitted symbols by sampling from the proposed Langevin dynamic. Furthermore, we carefully craft this stochastic dynamic by gradually adding a sequence of noise with decreasing variance to the trajectories, which ensures that the estimated symbols belong to a pre-specified discrete constellation. Through numerical experiments, we show that our proposed detector yields state-of-the-art symbol error rate performance.