Gunnar Carlsson
Position Paper: Challenges and Opportunities in Topological Deep Learning
Feb 14, 2024
Abstract:Topological deep learning (TDL) is a rapidly evolving field that uses topological features to understand and design deep learning models. This paper posits that TDL may complement graph representation learning and geometric deep learning by incorporating topological concepts, and can thus provide a natural choice for various machine learning settings. To this end, this paper discusses open problems in TDL, ranging from practical benefits to theoretical foundations. For each problem, it outlines potential solutions and future research opportunities. At the same time, this paper serves as an invitation to the scientific community to actively participate in TDL research to unlock the potential of this emerging field.
Current Topological and Machine Learning Applications for Bias Detection in Text
Nov 22, 2023



Abstract:Institutional bias can impact patient outcomes, educational attainment, and legal system navigation. Written records often reflect bias, and once bias is identified; it is possible to refer individuals for training to reduce bias. Many machine learning tools exist to explore text data and create predictive models that can search written records to identify real-time bias. However, few previous studies investigate large language model embeddings and geometric models of biased text data to understand geometry's impact on bias modeling accuracy. To overcome this issue, this study utilizes the RedditBias database to analyze textual biases. Four transformer models, including BERT and RoBERTa variants, were explored. Post-embedding, t-SNE allowed two-dimensional visualization of data. KNN classifiers differentiated bias types, with lower k-values proving more effective. Findings suggest BERT, particularly mini BERT, excels in bias classification, while multilingual models lag. The recommendation emphasizes refining monolingual models and exploring domain-specific biases.
Robust Hierarchical Clustering for Directed Networks: An Axiomatic Approach
Aug 16, 2021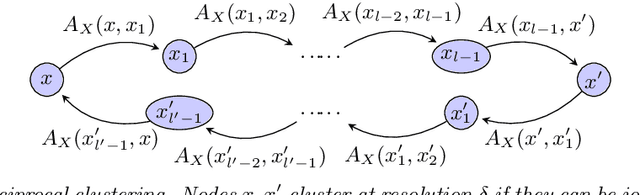

Abstract:We provide a complete taxonomic characterization of robust hierarchical clustering methods for directed networks following an axiomatic approach. We begin by introducing three practical properties associated with the notion of robustness in hierarchical clustering: linear scale preservation, stability, and excisiveness. Linear scale preservation enforces imperviousness to change in units of measure whereas stability ensures that a bounded perturbation in the input network entails a bounded perturbation in the clustering output. Excisiveness refers to the local consistency of the clustering outcome. Algorithmically, excisiveness implies that we can reduce computational complexity by only clustering a subset of our data while theoretically guaranteeing that the same hierarchical outcome would be observed when clustering the whole dataset. In parallel to these three properties, we introduce the concept of representability, a generative model for describing clustering methods through the specification of their action on a collection of networks. Our main result is to leverage this generative model to give a precise characterization of all robust -- i.e., excisive, linear scale preserving, and stable -- hierarchical clustering methods for directed networks. We also address the implementation of our methods and describe an application to real data.
Topological Deep Learning
Jan 14, 2021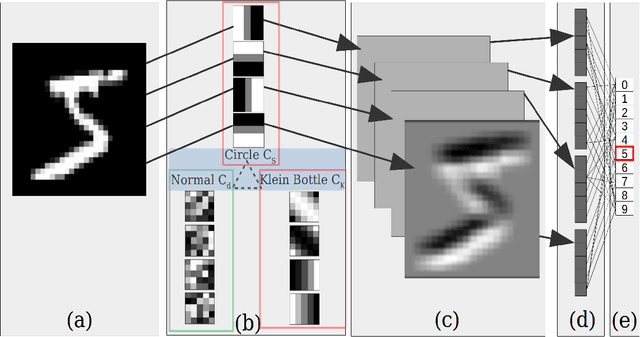

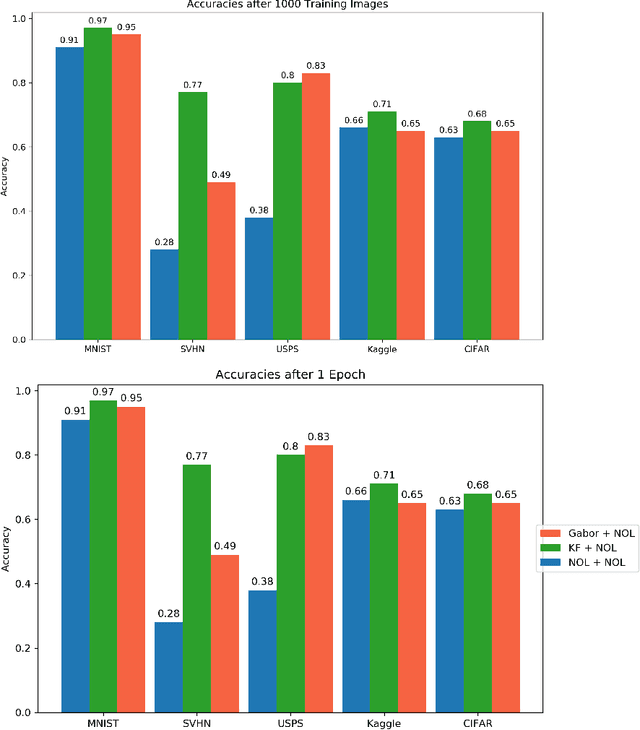

Abstract:This work introduces the Topological CNN (TCNN), which encompasses several topologically defined convolutional methods. Manifolds with important relationships to the natural image space are used to parameterize image filters which are used as convolutional weights in a TCNN. These manifolds also parameterize slices in layers of a TCNN across which the weights are localized. We show evidence that TCNNs learn faster, on less data, with fewer learned parameters, and with greater generalizability and interpretability than conventional CNNs. We introduce and explore TCNN layers for both image and video data. We propose extensions to 3D images and 3D video.
The space of sections of a smooth function
Jun 22, 2020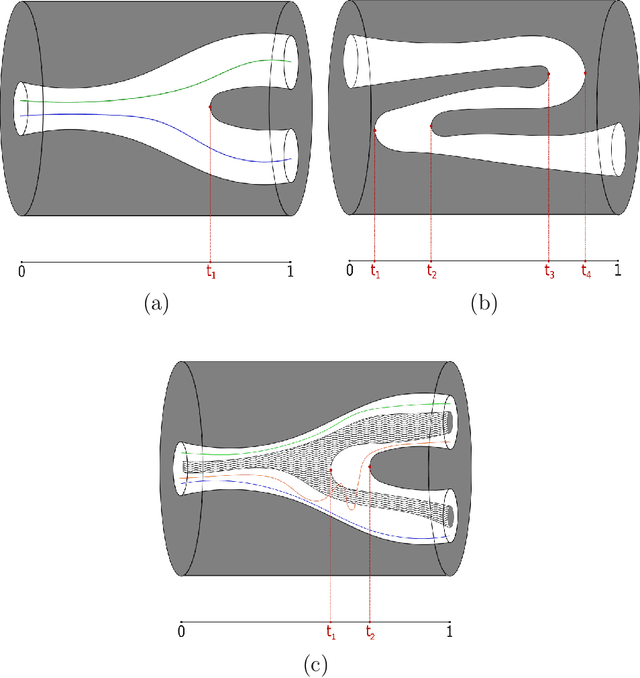
Abstract:Given a compact manifold $X$ with boundary and a submersion $f : X \rightarrow Y$ whose restriction to the boundary of $X$ has isolated critical points with distinct critical values and where $Y$ is $[0,1]$ or $S^1$, the connected components of the space of sections of $f$ are computed from $\pi_0$ and $\pi_1$ of the fibers of $f$. This computation is then leveraged to provide new results on a smoothed version of the evasion path problem for mobile sensor networks: From the time-varying homology of the covered region and the time-varying cup-product on cohomology of the boundary, a necessary and sufficient condition for existence of an evasion path and a lower bound on the number of homotopy classes of evasion paths are computed. No connectivity assumptions are required.
A Topology Layer for Machine Learning
May 29, 2019
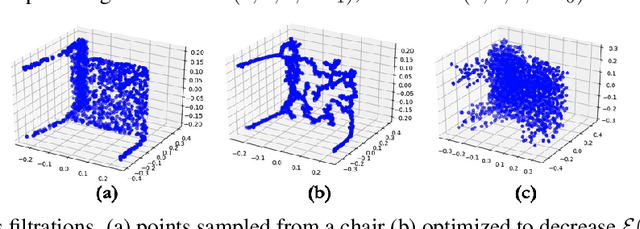

Abstract:Topology applied to real world data using persistent homology has started to find applications within machine learning, including deep learning. We present a differentiable topology layer that computes persistent homology based on level set filtrations and distance-bases filtrations. We present three novel applications: the topological layer can (i) serve as a regularizer directly on data or the weights of machine learning models, (ii) construct a loss on the output of a deep generative network to incorporate topological priors, and (iii) perform topological adversarial attacks on deep networks trained with persistence features. The code is publicly available and we hope its availability will facilitate the use of persistent homology in deep learning and other gradient based applications.
Topological Approaches to Deep Learning
Nov 02, 2018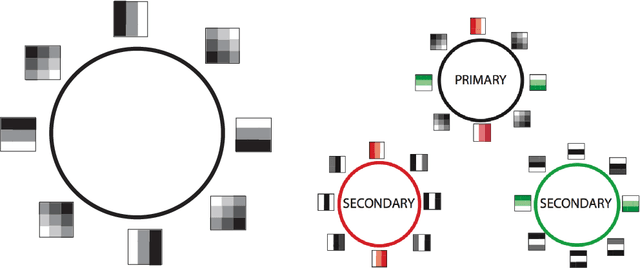

Abstract:We perform topological data analysis on the internal states of convolutional deep neural networks to develop an understanding of the computations that they perform. We apply this understanding to modify the computations so as to (a) speed up computations and (b) improve generalization from one data set of digits to another. One byproduct of the analysis is the production of a geometry on new sets of features on data sets of images, and use this observation to develop a methodology for constructing analogues of CNN's for many other geometries, including the graph structures constructed by topological data analysis.
A look at the topology of convolutional neural networks
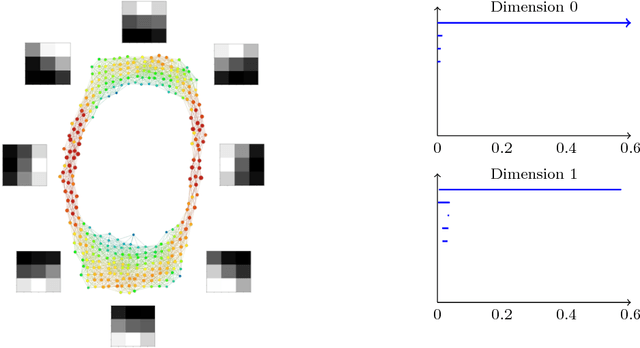
Oct 08, 2018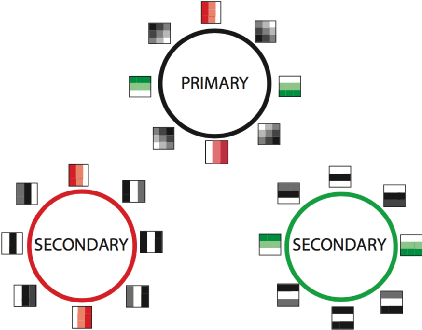


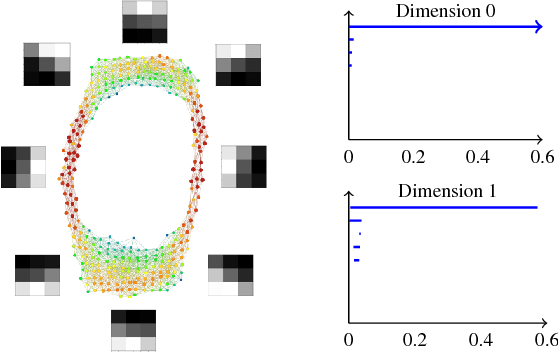
Abstract:Convolutional neural networks (CNN's) are powerful and widely used tools. However, their interpretability is far from ideal. In this paper we use topological data analysis to investigate what various CNN's learn. We show that the weights of convolutional layers at depths from 1 through 13 learn simple global structures. We also demonstrate the change of the simple structures over the course of training. In particular, we define and analyze the spaces of spatial filters of convolutional layers and show the recurrence, among all networks, depths, and during training, of a simple circle consisting of rotating edges, as well as a less recurring unanticipated complex circle that combines lines, edges, and non-linear patterns. We train over a thousand CNN's on MNIST and CIFAR-10, as well as use VGG-networks pretrained on ImageNet.
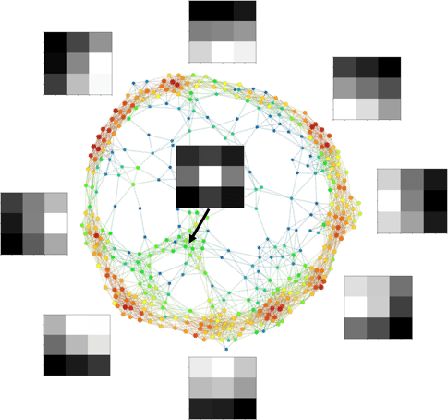
Fibres of Failure: Classifying errors in predictive processes
Feb 09, 2018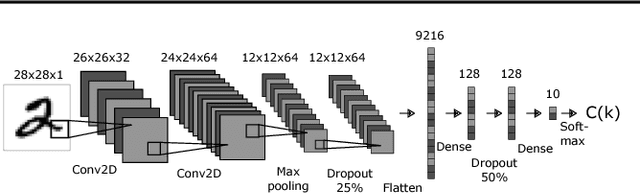
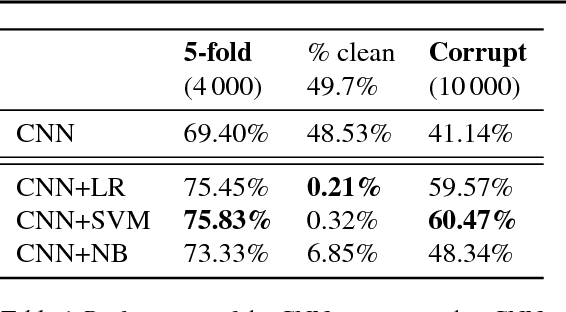
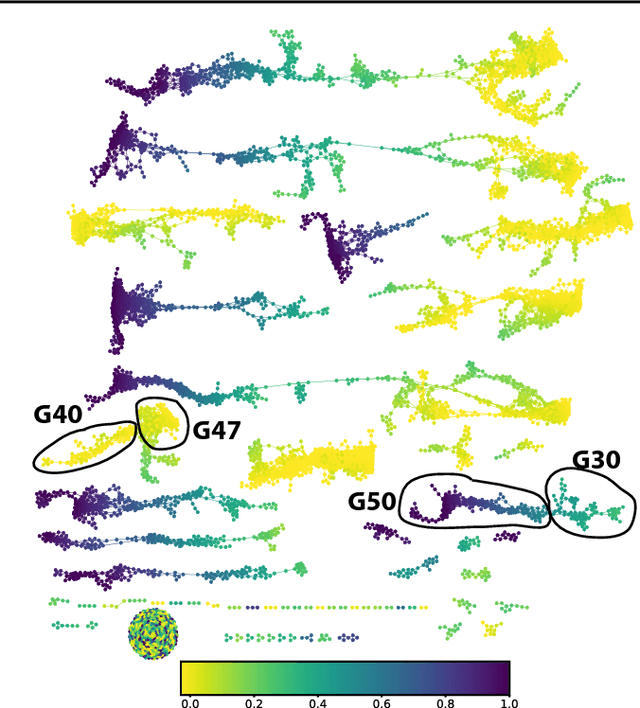
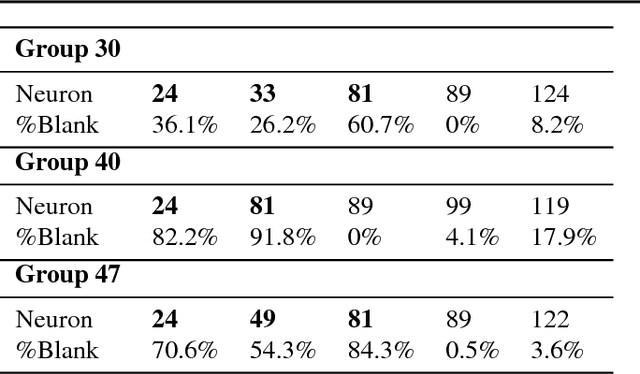
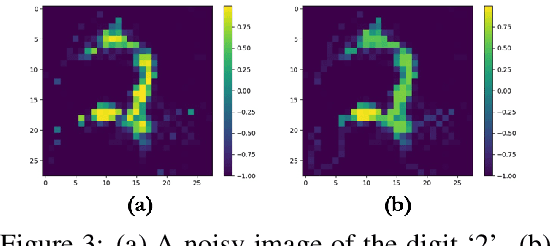
Abstract:We describe Fibres of Failure (FiFa), a method to classify failure modes of predictive processes using the Mapper algorithm from Topological Data Analysis. Our method uses Mapper to build a graph model of input data stratified by prediction error. Groupings found in high-error regions of the Mapper model then provide distinct failure modes of the predictive process. We demonstrate FiFa on misclassifications of MNIST images with added noise, and demonstrate two ways to use the failure mode classification: either to produce a correction layer that adjusts predictions by similarity to the failure modes; or to inspect members of the failure modes to illustrate and investigate what characterizes each failure mode.
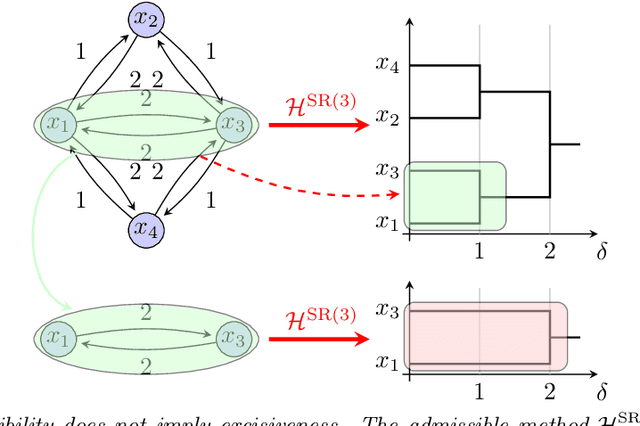
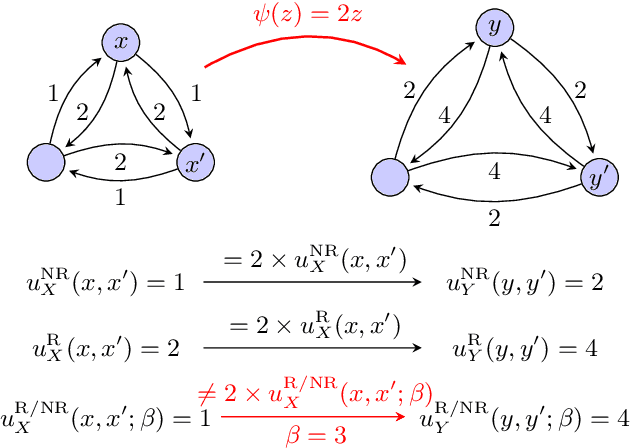
Excisive Hierarchical Clustering Methods for Network Data
Jul 21, 2016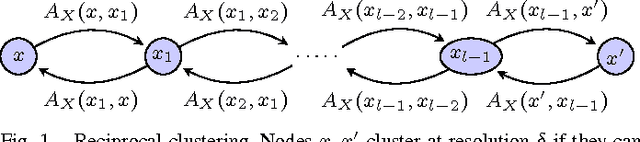
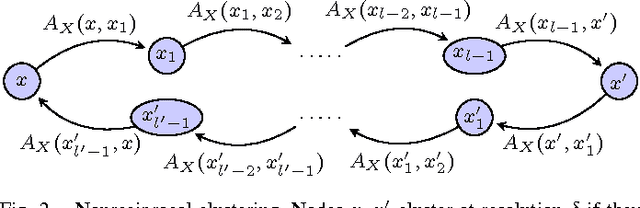
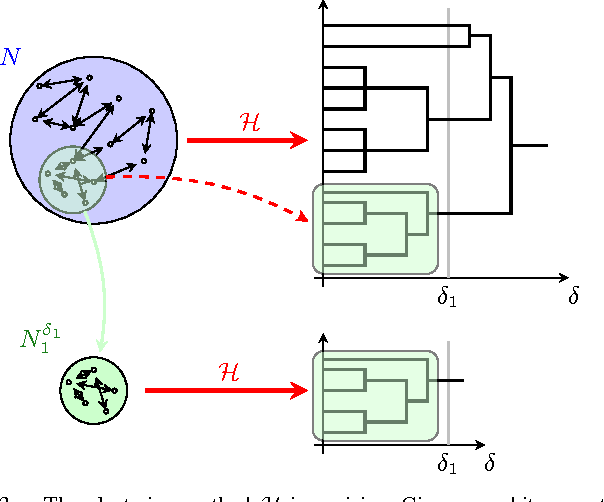
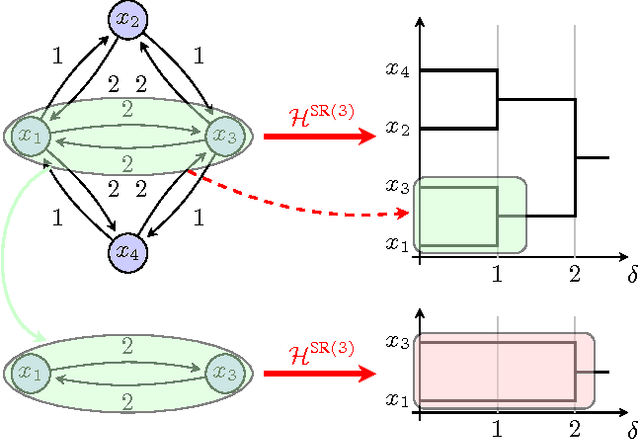
Abstract:We introduce two practical properties of hierarchical clustering methods for (possibly asymmetric) network data: excisiveness and linear scale preservation. The latter enforces imperviousness to change in units of measure whereas the former ensures local consistency of the clustering outcome. Algorithmically, excisiveness implies that we can reduce computational complexity by only clustering a data subset of interest while theoretically guaranteeing that the same hierarchical outcome would be observed when clustering the whole dataset. Moreover, we introduce the concept of representability, i.e. a generative model for describing clustering methods through the specification of their action on a collection of networks. We further show that, within a rich set of admissible methods, requiring representability is equivalent to requiring both excisiveness and linear scale preservation. Leveraging this equivalence, we show that all excisive and linear scale preserving methods can be factored into two steps: a transformation of the weights in the input network followed by the application of a canonical clustering method. Furthermore, their factorization can be used to show stability of excisive and linear scale preserving methods in the sense that a bounded perturbation in the input network entails a bounded perturbation in the clustering output.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge