The Z-Gromov-Wasserstein Distance

The Gromov-Wasserstein (GW) distance is a powerful tool for comparing metric measure spaces which has found broad applications in data science and machine learning. Driven by the need to analyze datasets whose objects have increasingly complex structure (such as node and edge-attributed graphs), several variants of GW distance have been introduced in the recent literature. With a view toward establishing a general framework for the theory of GW-like distances, this paper considers a vast generalization of the notion of a metric measure space: for an arbitrary metric space $Z$, we define a $Z$-network to be a measure space endowed with a kernel valued in $Z$. We introduce a method for comparing $Z$-networks by defining a generalization of GW distance, which we refer to as $Z$-Gromov-Wasserstein ($Z$-GW) distance. This construction subsumes many previously known metrics and offers a unified approach to understanding their shared properties. The paper demonstrates that the $Z$-GW distance defines a metric on the space of $Z$-networks which retains desirable properties of $Z$, such as separability, completeness, and geodesicity. Many of these properties were unknown for existing variants of GW distance that fall under our framework. Our focus is on foundational theory, but our results also include computable lower bounds and approximations of the distance which will be useful for practical applications.

Geometry and Stability of Supervised Learning Problems

We introduce a notion of distance between supervised learning problems, which we call the Risk distance. This optimal-transport-inspired distance facilitates stability results; one can quantify how seriously issues like sampling bias, noise, limited data, and approximations might change a given problem by bounding how much these modifications can move the problem under the Risk distance. With the distance established, we explore the geometry of the resulting space of supervised learning problems, providing explicit geodesics and proving that the set of classification problems is dense in a larger class of problems. We also provide two variants of the Risk distance: one that incorporates specified weights on a problem's predictors, and one that is more sensitive to the contours of a problem's risk landscape.

The Weisfeiler-Lehman Distance: Reinterpretation and Connection with GNNs

In this paper, we present a novel interpretation of the so-called Weisfeiler-Lehman (WL) distance, introduced by Chen et al. (2022), using concepts from stochastic processes. The WL distance aims at comparing graphs with node features, has the same discriminative power as the classic Weisfeiler-Lehman graph isomorphism test and has deep connections to the Gromov-Wasserstein distance. This new interpretation connects the WL distance to the literature on distances for stochastic processes, which also makes the interpretation of the distance more accessible and intuitive. We further explore the connections between the WL distance and certain Message Passing Neural Networks, and discuss the implications of the WL distance for understanding the Lipschitz property and the universal approximation results for these networks.

Weisfeiler-Lehman meets Gromov-Wasserstein

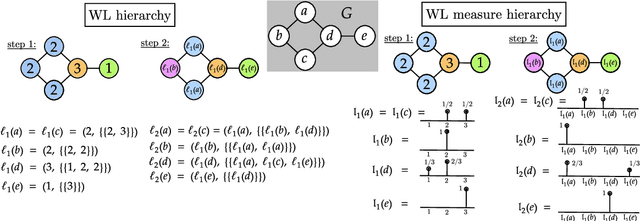
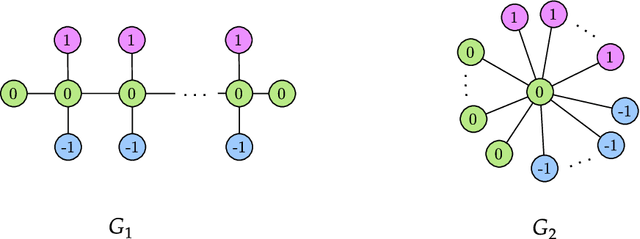
The Weisfeiler-Lehman (WL) test is a classical procedure for graph isomorphism testing. The WL test has also been widely used both for designing graph kernels and for analyzing graph neural networks. In this paper, we propose the Weisfeiler-Lehman (WL) distance, a notion of distance between labeled measure Markov chains (LMMCs), of which labeled graphs are special cases. The WL distance is polynomial time computable and is also compatible with the WL test in the sense that the former is positive if and only if the WL test can distinguish the two involved graphs. The WL distance captures and compares subtle structures of the underlying LMMCs and, as a consequence of this, it is more discriminating than the distance between graphs used for defining the state-of-the-art Wasserstein Weisfeiler-Lehman graph kernel. Inspired by the structure of the WL distance we identify a neural network architecture on LMMCs which turns out to be universal w.r.t. continuous functions defined on the space of all LMMCs (which includes all graphs) endowed with the WL distance. Finally, the WL distance turns out to be stable w.r.t. a natural variant of the Gromov-Wasserstein (GW) distance for comparing metric Markov chains that we identify. Hence, the WL distance can also be construed as a polynomial time lower bound for the GW distance which is in general NP-hard to compute.

Robust Hierarchical Clustering for Directed Networks: An Axiomatic Approach

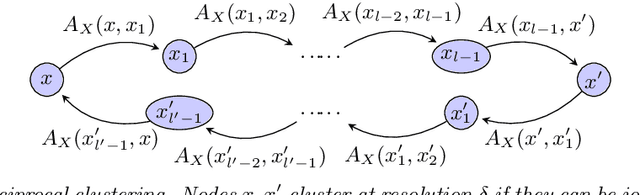
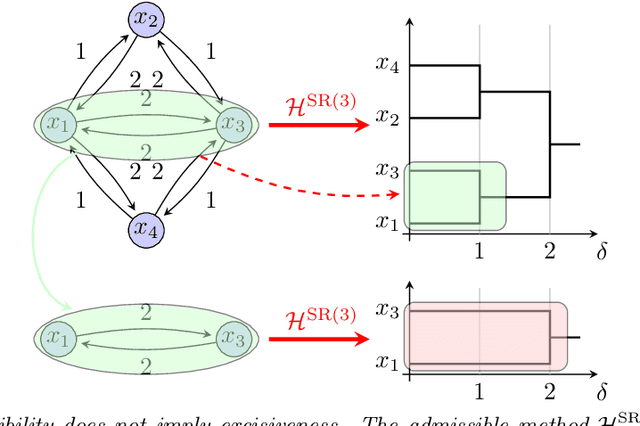
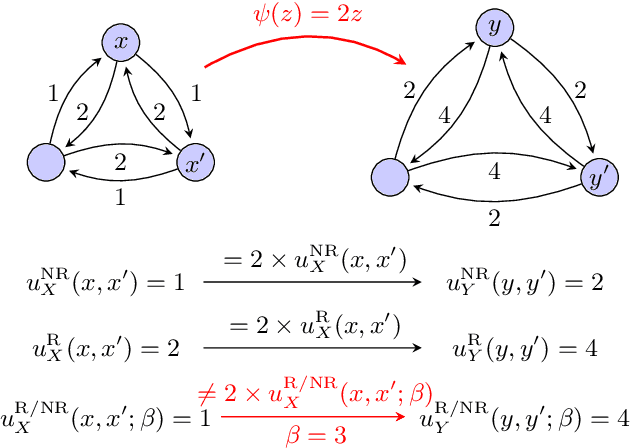
We provide a complete taxonomic characterization of robust hierarchical clustering methods for directed networks following an axiomatic approach. We begin by introducing three practical properties associated with the notion of robustness in hierarchical clustering: linear scale preservation, stability, and excisiveness. Linear scale preservation enforces imperviousness to change in units of measure whereas stability ensures that a bounded perturbation in the input network entails a bounded perturbation in the clustering output. Excisiveness refers to the local consistency of the clustering outcome. Algorithmically, excisiveness implies that we can reduce computational complexity by only clustering a subset of our data while theoretically guaranteeing that the same hierarchical outcome would be observed when clustering the whole dataset. In parallel to these three properties, we introduce the concept of representability, a generative model for describing clustering methods through the specification of their action on a collection of networks. Our main result is to leverage this generative model to give a precise characterization of all robust -- i.e., excisive, linear scale preserving, and stable -- hierarchical clustering methods for directed networks. We also address the implementation of our methods and describe an application to real data.

The Gaussian Transform

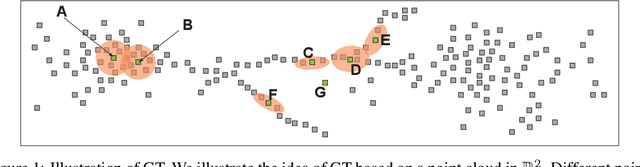
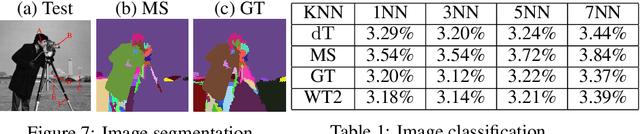
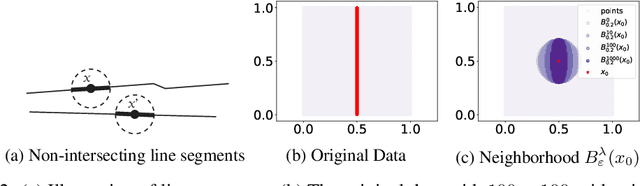
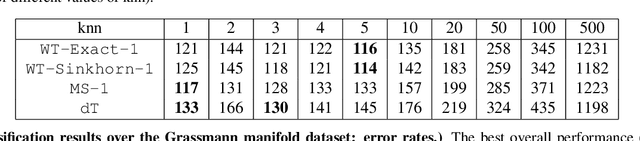
We introduce the Gaussian transform (GT), an optimal transport inspired iterative method for denoising and enhancing latent structures in datasets. Under the hood, GT generates a new distance function (GT distance) on a given dataset by computing the $\ell^2$-Wasserstein distance between certain Gaussian density estimates obtained by localizing the dataset to individual points. Our contribution is twofold: (1) theoretically, we establish firstly that GT is stable under perturbations and secondly that in the continuous case, each point possesses an asymptotically ellipsoidal neighborhood with respect to the GT distance; (2) computationally, we accelerate GT both by identifying a strategy for reducing the number of matrix square root computations inherent to the $\ell^2$-Wasserstein distance between Gaussian measures, and by avoiding redundant computations of GT distances between points via enhanced neighborhood mechanisms. We also observe that GT is both a generalization and a strengthening of the mean shift (MS) method, and it is also a computationally efficient specialization of the recently proposed Wasserstein Transform (WT) method. We perform extensive experimentation comparing their performance in different scenarios.

Motivic clustering schemes for directed graphs

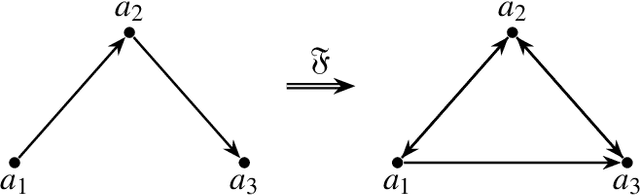
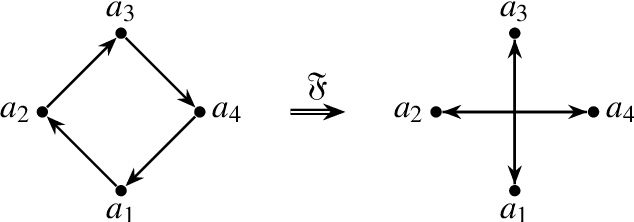
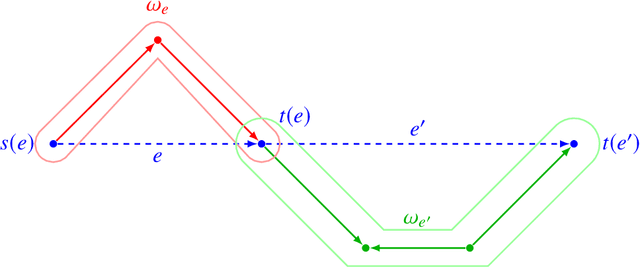
Motivated by the concept of network motifs we construct certain clustering methods (functors) which are parametrized by a given collection of motifs (or representers).

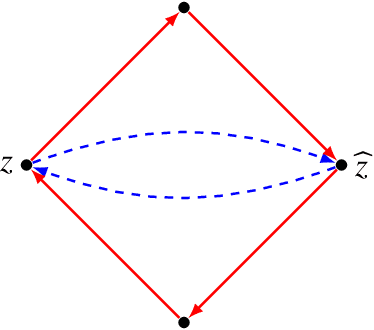
The Wasserstein transform

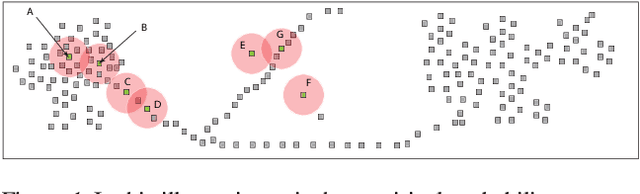
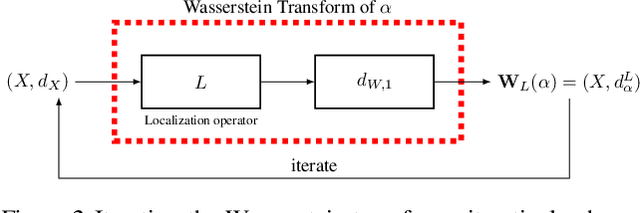
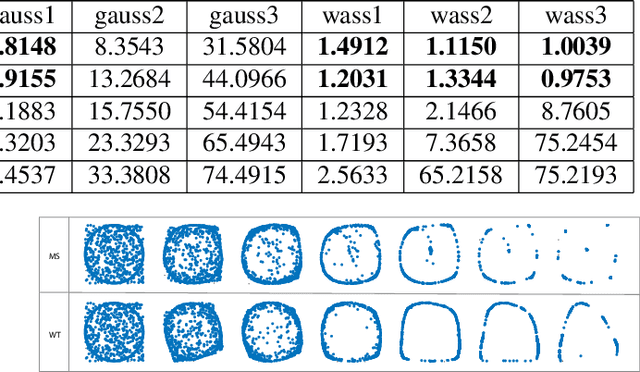
We introduce the Wasserstein transform, a method for enhancing and denoising datasets defined on general metric spaces. The construction draws inspiration from Optimal Transportation ideas. We establish precise connections with the mean shift family of algorithms and establish the stability of both our method and mean shift under data perturbation.

The Shape of Data and Probability Measures

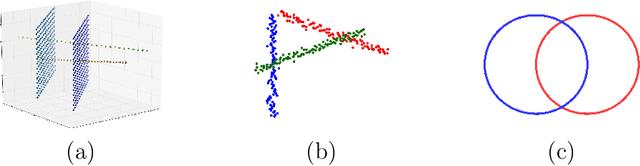
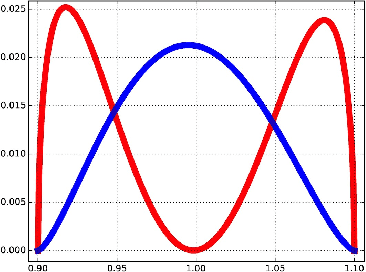
We introduce the notion of multiscale covariance tensor fields (CTF) associated with Euclidean random variables as a gateway to the shape of their distributions. Multiscale CTFs quantify variation of the data about every point in the data landscape at all spatial scales, unlike the usual covariance tensor that only quantifies global variation about the mean. Empirical forms of localized covariance previously have been used in data analysis and visualization, but we develop a framework for the systematic treatment of theoretical questions and computational models based on localized covariance. We prove strong stability theorems with respect to the Wasserstein distance between probability measures, obtain consistency results, as well as estimates for the rate of convergence of empirical CTFs. These results ensure that CTFs are robust to sampling, noise and outliers. We provide numerous illustrations of how CTFs let us extract shape from data and also apply CTFs to manifold clustering, the problem of categorizing data points according to their noisy membership in a collection of possibly intersecting, smooth submanifolds of Euclidean space. We prove that the proposed manifold clustering method is stable and carry out several experiments to validate the method.

Excisive Hierarchical Clustering Methods for Network Data

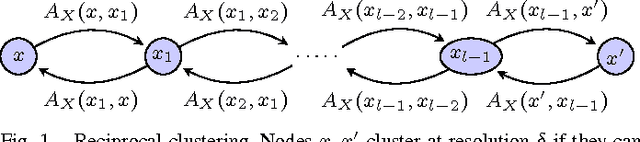
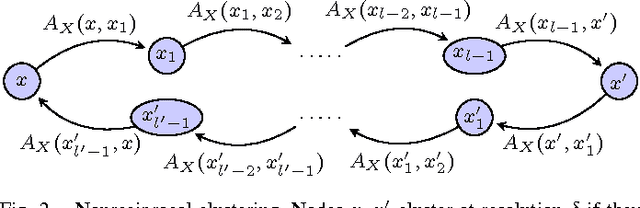
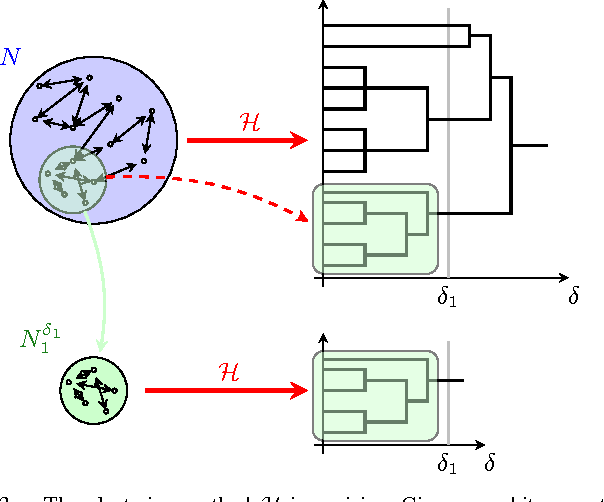
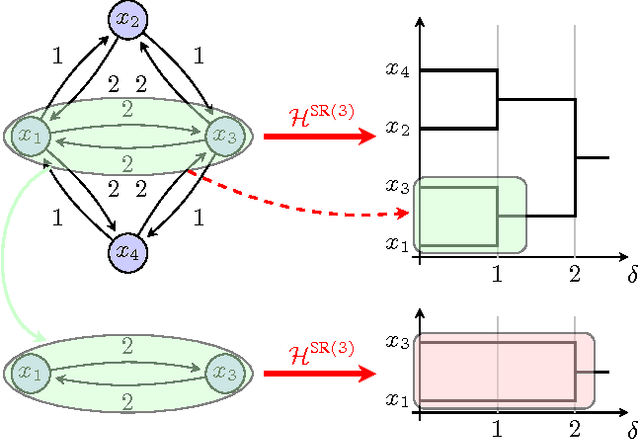
We introduce two practical properties of hierarchical clustering methods for (possibly asymmetric) network data: excisiveness and linear scale preservation. The latter enforces imperviousness to change in units of measure whereas the former ensures local consistency of the clustering outcome. Algorithmically, excisiveness implies that we can reduce computational complexity by only clustering a data subset of interest while theoretically guaranteeing that the same hierarchical outcome would be observed when clustering the whole dataset. Moreover, we introduce the concept of representability, i.e. a generative model for describing clustering methods through the specification of their action on a collection of networks. We further show that, within a rich set of admissible methods, requiring representability is equivalent to requiring both excisiveness and linear scale preservation. Leveraging this equivalence, we show that all excisive and linear scale preserving methods can be factored into two steps: a transformation of the weights in the input network followed by the application of a canonical clustering method. Furthermore, their factorization can be used to show stability of excisive and linear scale preserving methods in the sense that a bounded perturbation in the input network entails a bounded perturbation in the clustering output.