Task-Specific Skill Localization in Fine-tuned Language Models

Pre-trained language models can be fine-tuned to solve diverse NLP tasks, including in few-shot settings. Thus fine-tuning allows the model to quickly pick up task-specific ``skills,'' but there has been limited study of where these newly-learnt skills reside inside the massive model. This paper introduces the term skill localization for this problem and proposes a solution. Given the downstream task and a model fine-tuned on that task, a simple optimization is used to identify a very small subset of parameters ($\sim0.01$% of model parameters) responsible for ($>95$%) of the model's performance, in the sense that grafting the fine-tuned values for just this tiny subset onto the pre-trained model gives performance almost as well as the fine-tuned model. While reminiscent of recent works on parameter-efficient fine-tuning, the novel aspects here are that: (i) No further re-training is needed on the subset (unlike, say, with lottery tickets). (ii) Notable improvements are seen over vanilla fine-tuning with respect to calibration of predictions in-distribution ($40$-$90$% error reduction) as well as the quality of predictions out-of-distribution (OOD). In models trained on multiple tasks, a stronger notion of skill localization is observed, where the sparse regions corresponding to different tasks are almost disjoint, and their overlap (when it happens) is a proxy for task similarity. Experiments suggest that localization via grafting can assist certain forms of continual learning.

New Definitions and Evaluations for Saliency Methods: Staying Intrinsic, Complete and Sound

Saliency methods compute heat maps that highlight portions of an input that were most {\em important} for the label assigned to it by a deep net. Evaluations of saliency methods convert this heat map into a new {\em masked input} by retaining the $k$ highest-ranked pixels of the original input and replacing the rest with \textquotedblleft uninformative\textquotedblright\ pixels, and checking if the net's output is mostly unchanged. This is usually seen as an {\em explanation} of the output, but the current paper highlights reasons why this inference of causality may be suspect. Inspired by logic concepts of {\em completeness \& soundness}, it observes that the above type of evaluation focuses on completeness of the explanation, but ignores soundness. New evaluation metrics are introduced to capture both notions, while staying in an {\em intrinsic} framework -- i.e., using the dataset and the net, but no separately trained nets, human evaluations, etc. A simple saliency method is described that matches or outperforms prior methods in the evaluations. Experiments also suggest new intrinsic justifications, based on soundness, for popular heuristic tricks such as TV regularization and upsampling.

A Kernel-Based View of Language Model Fine-Tuning

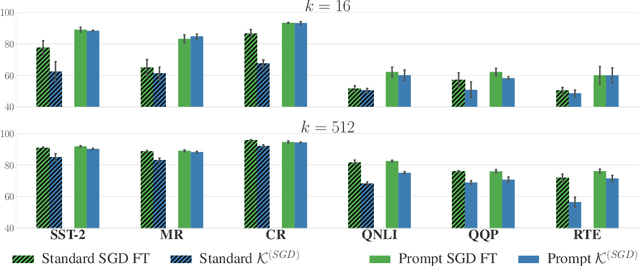
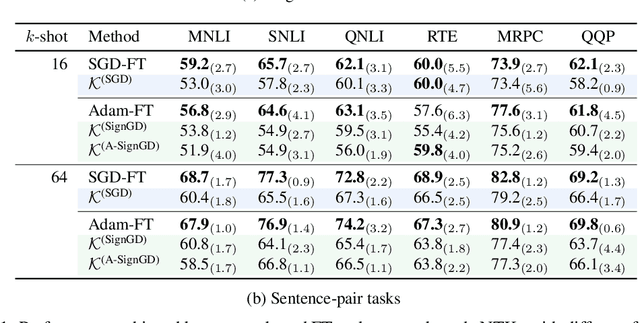
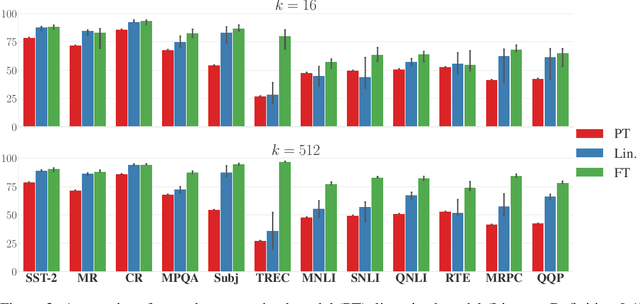
It has become standard to solve NLP tasks by fine-tuning pre-trained language models (LMs), especially in low-data settings. There is minimal theoretical understanding of empirical success, e.g., why fine-tuning a model with $10^8$ or more parameters on a couple dozen training points does not result in overfitting. We investigate whether the Neural Tangent Kernel (NTK) - which originated as a model to study the gradient descent dynamics of infinitely wide networks with suitable random initialization - describes fine-tuning of pre-trained LMs. This study was inspired by the decent performance of NTK for computer vision tasks (Wei et al., 2022). We also extend the NTK formalism to fine-tuning with Adam. We present extensive experiments that show that once the downstream task is formulated as a language modeling problem through prompting, the NTK lens can often reasonably describe the model updates during fine-tuning with both SGD and Adam. This kernel view also suggests an explanation for success of parameter-efficient subspace-based fine-tuning methods. Finally, we suggest a path toward a formal explanation for our findings via Tensor Programs (Yang, 2020).

Understanding Influence Functions and Datamodels via Harmonic Analysis

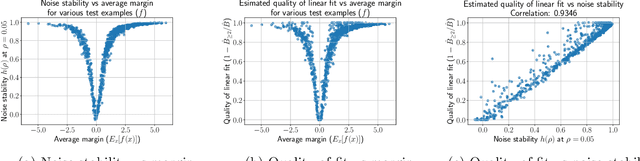
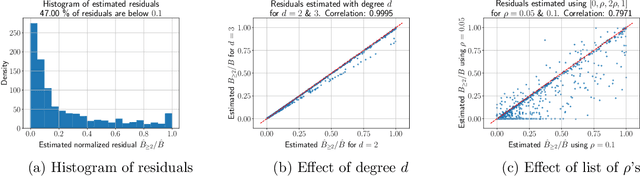
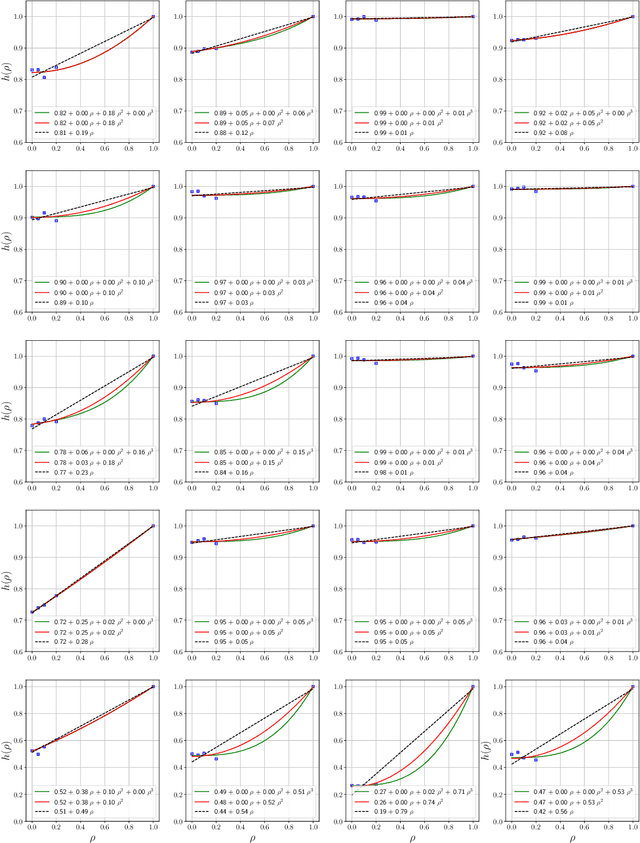
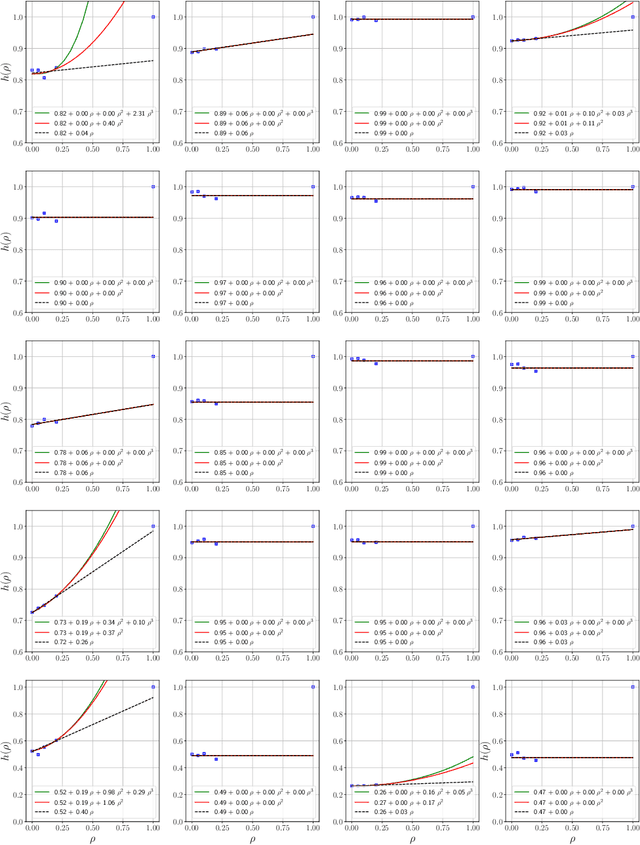
Influence functions estimate effect of individual data points on predictions of the model on test data and were adapted to deep learning in Koh and Liang [2017]. They have been used for detecting data poisoning, detecting helpful and harmful examples, influence of groups of datapoints, etc. Recently, Ilyas et al. [2022] introduced a linear regression method they termed datamodels to predict the effect of training points on outputs on test data. The current paper seeks to provide a better theoretical understanding of such interesting empirical phenomena. The primary tool is harmonic analysis and the idea of noise stability. Contributions include: (a) Exact characterization of the learnt datamodel in terms of Fourier coefficients. (b) An efficient method to estimate the residual error and quality of the optimum linear datamodel without having to train the datamodel. (c) New insights into when influences of groups of datapoints may or may not add up linearly.

Implicit Bias of Gradient Descent on Reparametrized Models: On Equivalence to Mirror Descent

As part of the effort to understand implicit bias of gradient descent in overparametrized models, several results have shown how the training trajectory on the overparametrized model can be understood as mirror descent on a different objective. The main result here is a characterization of this phenomenon under a notion termed commuting parametrization, which encompasses all the previous results in this setting. It is shown that gradient flow with any commuting parametrization is equivalent to continuous mirror descent with a related Legendre function. Conversely, continuous mirror descent with any Legendre function can be viewed as gradient flow with a related commuting parametrization. The latter result relies upon Nash's embedding theorem.

Understanding the Generalization Benefit of Normalization Layers: Sharpness Reduction

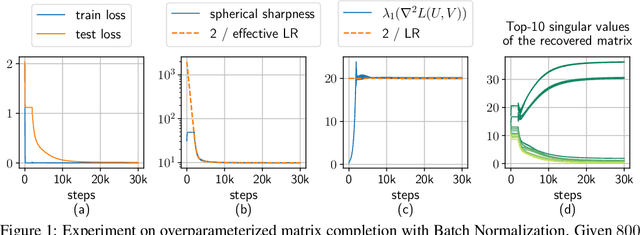
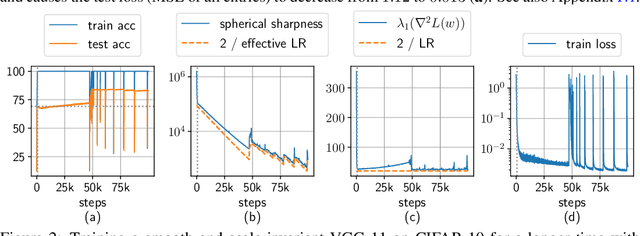
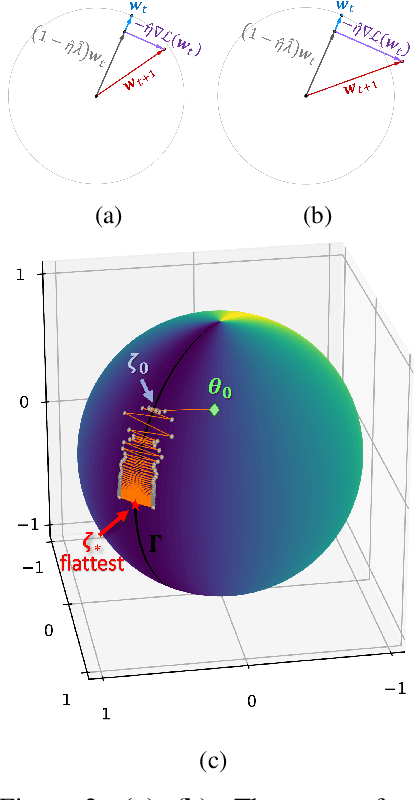
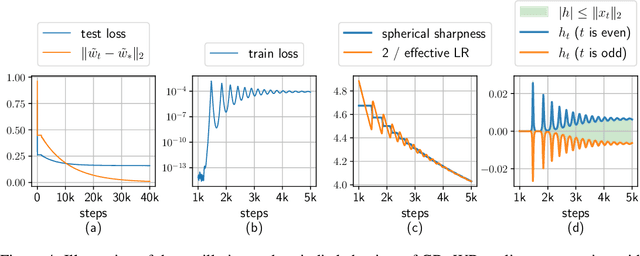
Normalization layers (e.g., Batch Normalization, Layer Normalization) were introduced to help with optimization difficulties in very deep nets, but they clearly also help generalization, even in not-so-deep nets. Motivated by the long-held belief that flatter minima lead to better generalization, this paper gives mathematical analysis and supporting experiments suggesting that normalization (together with accompanying weight-decay) encourages GD to reduce the sharpness of loss surface. Here "sharpness" is carefully defined given that the loss is scale-invariant, a known consequence of normalization. Specifically, for a fairly broad class of neural nets with normalization, our theory explains how GD with a finite learning rate enters the so-called Edge of Stability (EoS) regime, and characterizes the trajectory of GD in this regime via a continuous sharpness-reduction flow.

On the SDEs and Scaling Rules for Adaptive Gradient Algorithms

Approximating Stochastic Gradient Descent (SGD) as a Stochastic Differential Equation (SDE) has allowed researchers to enjoy the benefits of studying a continuous optimization trajectory while carefully preserving the stochasticity of SGD. Analogous study of adaptive gradient methods, such as RMSprop and Adam, has been challenging because there were no rigorously proven SDE approximations for these methods. This paper derives the SDE approximations for RMSprop and Adam, giving theoretical guarantees of their correctness as well as experimental validation of their applicability to common large-scaling vision and language settings. A key practical result is the derivation of a $\textit{square root scaling rule}$ to adjust the optimization hyperparameters of RMSprop and Adam when changing batch size, and its empirical validation in deep learning settings.

Understanding Gradient Descent on Edge of Stability in Deep Learning

Deep learning experiments in Cohen et al. (2021) using deterministic Gradient Descent (GD) revealed an {\em Edge of Stability (EoS)} phase when learning rate (LR) and sharpness (\emph{i.e.}, the largest eigenvalue of Hessian) no longer behave as in traditional optimization. Sharpness stabilizes around $2/$LR and loss goes up and down across iterations, yet still with an overall downward trend. The current paper mathematically analyzes a new mechanism of implicit regularization in the EoS phase, whereby GD updates due to non-smooth loss landscape turn out to evolve along some deterministic flow on the manifold of minimum loss. This is in contrast to many previous results about implicit bias either relying on infinitesimal updates or noise in gradient. Formally, for any smooth function $L$ with certain regularity condition, this effect is demonstrated for (1) {\em Normalized GD}, i.e., GD with a varying LR $ \eta_t =\frac{ \eta }{ || \nabla L(x(t)) || } $ and loss $L$; (2) GD with constant LR and loss $\sqrt{L}$. Both provably enter the Edge of Stability, with the associated flow on the manifold minimizing $\lambda_{\max}(\nabla^2 L)$. The above theoretical results have been corroborated by an experimental study.

Adaptive Gradient Methods with Local Guarantees

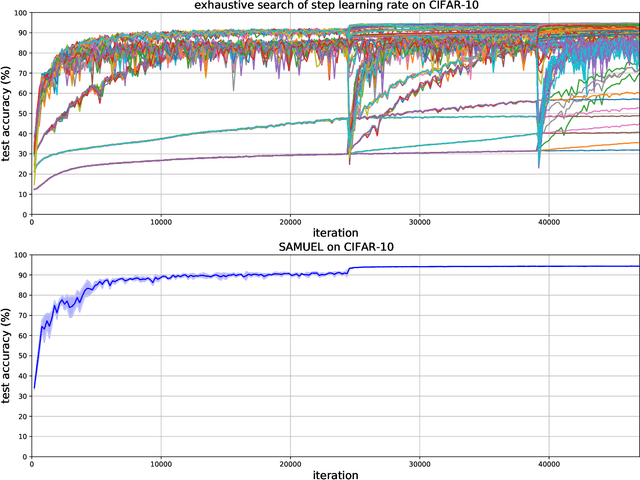
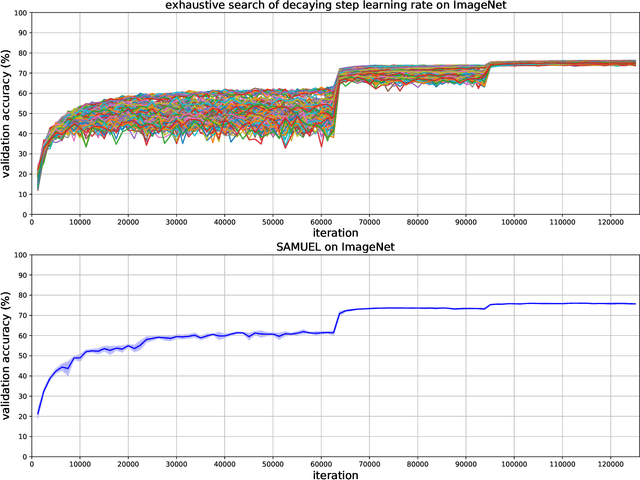
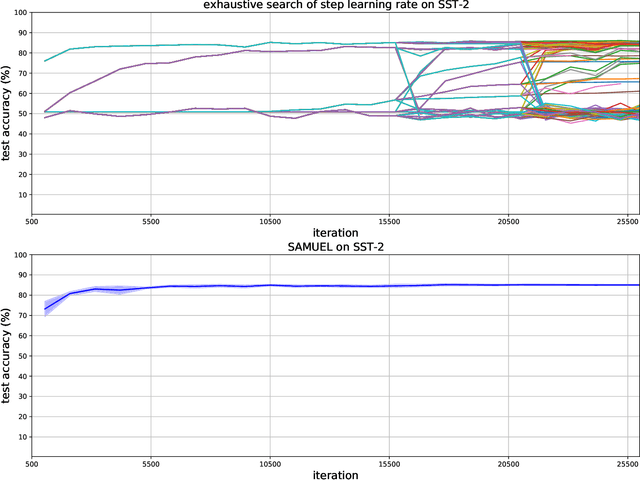
Adaptive gradient methods are the method of choice for optimization in machine learning and used to train the largest deep models. In this paper we study the problem of learning a local preconditioner, that can change as the data is changing along the optimization trajectory. We propose an adaptive gradient method that has provable adaptive regret guarantees vs. the best local preconditioner. To derive this guarantee, we prove a new adaptive regret bound in online learning that improves upon previous adaptive online learning methods. We demonstrate the robustness of our method in automatically choosing the optimal learning rate schedule for popular benchmarking tasks in vision and language domains. Without the need to manually tune a learning rate schedule, our method can, in a single run, achieve comparable and stable task accuracy as a fine-tuned optimizer.

Understanding Contrastive Learning Requires Incorporating Inductive Biases

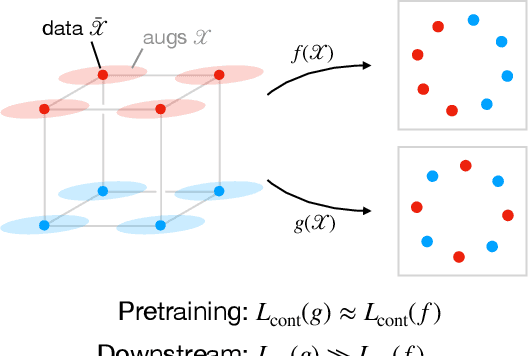
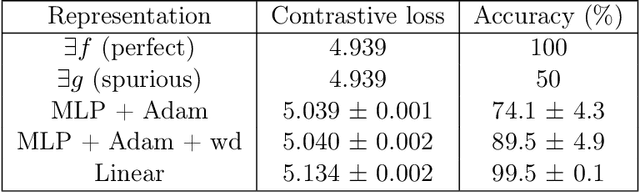
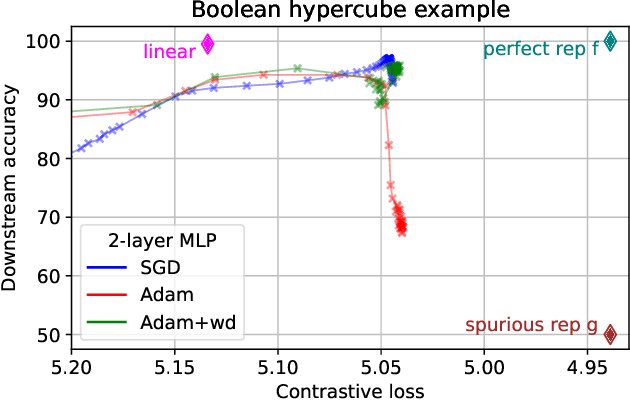
Contrastive learning is a popular form of self-supervised learning that encourages augmentations (views) of the same input to have more similar representations compared to augmentations of different inputs. Recent attempts to theoretically explain the success of contrastive learning on downstream classification tasks prove guarantees depending on properties of {\em augmentations} and the value of {\em contrastive loss} of representations. We demonstrate that such analyses, that ignore {\em inductive biases} of the function class and training algorithm, cannot adequately explain the success of contrastive learning, even {\em provably} leading to vacuous guarantees in some settings. Extensive experiments on image and text domains highlight the ubiquity of this problem -- different function classes and algorithms behave very differently on downstream tasks, despite having the same augmentations and contrastive losses. Theoretical analysis is presented for the class of linear representations, where incorporating inductive biases of the function class allows contrastive learning to work with less stringent conditions compared to prior analyses.