Solving Hidden Monotone Variational Inequalities with Surrogate Losses

Deep learning has proven to be effective in a wide variety of loss minimization problems. However, many applications of interest, like minimizing projected Bellman error and min-max optimization, cannot be modelled as minimizing a scalar loss function but instead correspond to solving a variational inequality (VI) problem. This difference in setting has caused many practical challenges as naive gradient-based approaches from supervised learning tend to diverge and cycle in the VI case. In this work, we propose a principled surrogate-based approach compatible with deep learning to solve VIs. We show that our surrogate-based approach has three main benefits: (1) under assumptions that are realistic in practice (when hidden monotone structure is present, interpolation, and sufficient optimization of the surrogates), it guarantees convergence, (2) it provides a unifying perspective of existing methods, and (3) is amenable to existing deep learning optimizers like ADAM. Experimentally, we demonstrate our surrogate-based approach is effective in min-max optimization and minimizing projected Bellman error. Furthermore, in the deep reinforcement learning case, we propose a novel variant of TD(0) which is more compute and sample efficient.

Abstracting Imperfect Information Away from Two-Player Zero-Sum Games

In their seminal work, Nayyar et al. (2013) showed that imperfect information can be abstracted away from common-payoff games by having players publicly announce their policies as they play. This insight underpins sound solvers and decision-time planning algorithms for common-payoff games. Unfortunately, a naive application of the same insight to two-player zero-sum games fails because Nash equilibria of the game with public policy announcements may not correspond to Nash equilibria of the original game. As a consequence, existing sound decision-time planning algorithms require complicated additional mechanisms that have unappealing properties. The main contribution of this work is showing that certain regularized equilibria do not possess the aforementioned non-correspondence problem -- thus, computing them can be treated as perfect information problems. Because these regularized equilibria can be made arbitrarily close to Nash equilibria, our result opens the door to a new perspective on solving two-player zero-sum games and, in particular, yields a simplified framework for decision-time planning in two-player zero-sum games, void of the unappealing properties that plague existing decision-time planning approaches.

A Unified Approach to Reinforcement Learning, Quantal Response Equilibria, and Two-Player Zero-Sum Games

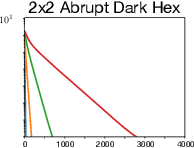
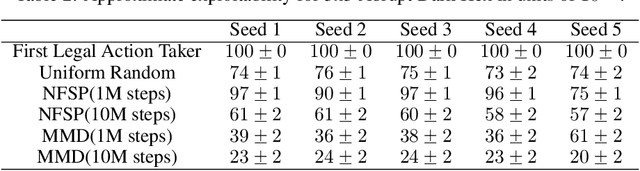
Algorithms designed for single-agent reinforcement learning (RL) generally fail to converge to equilibria in two-player zero-sum (2p0s) games. Conversely, game-theoretic algorithms for approximating Nash and quantal response equilibria (QREs) in 2p0s games are not typically competitive for RL and can be difficult to scale. As a result, algorithms for these two cases are generally developed and evaluated separately. In this work, we show that a single algorithm -- a simple extension to mirror descent with proximal regularization that we call magnetic mirror descent (MMD) -- can produce strong results in both settings, despite their fundamental differences. From a theoretical standpoint, we prove that MMD converges linearly to QREs in extensive-form games -- this is the first time linear convergence has been proven for a first order solver. Moreover, applied as a tabular Nash equilibrium solver via self-play, we show empirically that MMD produces results competitive with CFR in both normal-form and extensive-form games with full feedback (this is the first time that a standard RL algorithm has done so) and also that MMD empirically converges in black-box feedback settings. Furthermore, for single-agent deep RL, on a small collection of Atari and Mujoco games, we show that MMD can produce results competitive with those of PPO. Lastly, for multi-agent deep RL, we show MMD can outperform NFSP in 3x3 Abrupt Dark Hex.

Efficient Deviation Types and Learning for Hindsight Rationality in Extensive-Form Games: Corrections

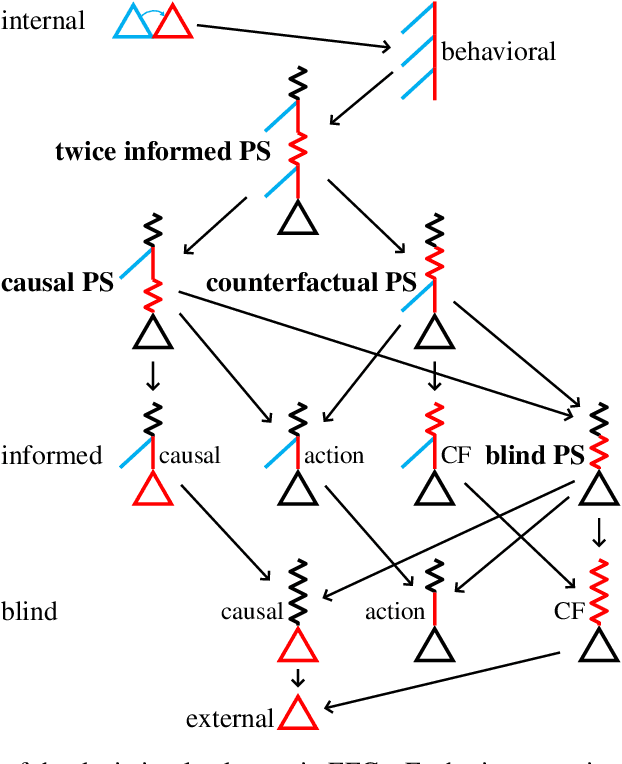
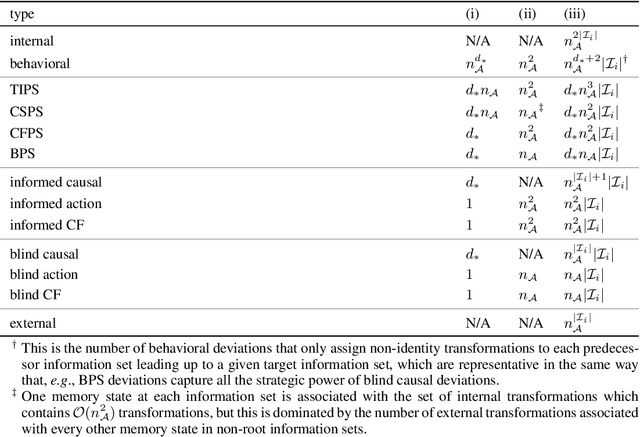
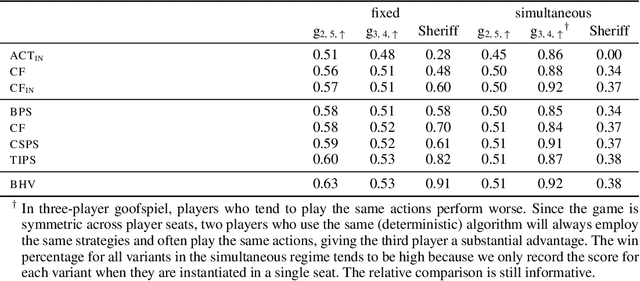
Hindsight rationality is an approach to playing general-sum games that prescribes no-regret learning dynamics for individual agents with respect to a set of deviations, and further describes jointly rational behavior among multiple agents with mediated equilibria. To develop hindsight rational learning in sequential decision-making settings, we formalize behavioral deviations as a general class of deviations that respect the structure of extensive-form games. Integrating the idea of time selection into counterfactual regret minimization (CFR), we introduce the extensive-form regret minimization (EFR) algorithm that achieves hindsight rationality for any given set of behavioral deviations with computation that scales closely with the complexity of the set. We identify behavioral deviation subsets, the partial sequence deviation types, that subsume previously studied types and lead to efficient EFR instances in games with moderate lengths. In addition, we present a thorough empirical analysis of EFR instantiated with different deviation types in benchmark games, where we find that stronger types typically induce better performance.

Stochastic Mirror Descent: Convergence Analysis and Adaptive Variants via the Mirror Stochastic Polyak Stepsize

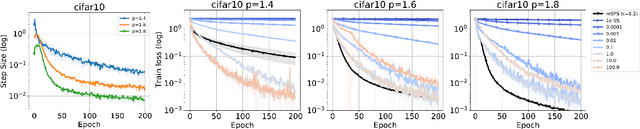
We investigate the convergence of stochastic mirror descent (SMD) in relatively smooth and smooth convex optimization. In relatively smooth convex optimization we provide new convergence guarantees for SMD with a constant stepsize. For smooth convex optimization we propose a new adaptive stepsize scheme -- the mirror stochastic Polyak stepsize (mSPS). Notably, our convergence results in both settings do not make bounded gradient assumptions or bounded variance assumptions, and we show convergence to a neighborhood that vanishes under interpolation. mSPS generalizes the recently proposed stochastic Polyak stepsize (SPS) (Loizou et al., 2021) to mirror descent and remains both practical and efficient for modern machine learning applications while inheriting the benefits of mirror descent. We complement our results with experiments across various supervised learning tasks and different instances of SMD, demonstrating the effectiveness of mSPS.

Efficient Deviation Types and Learning for Hindsight Rationality in Extensive-Form Games

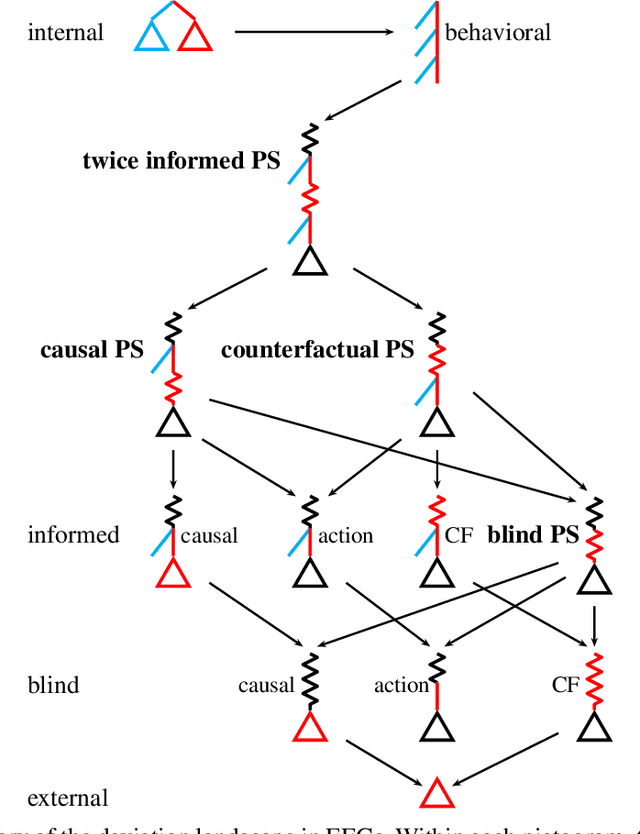
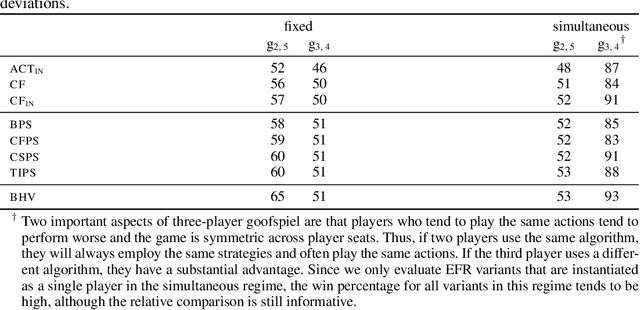
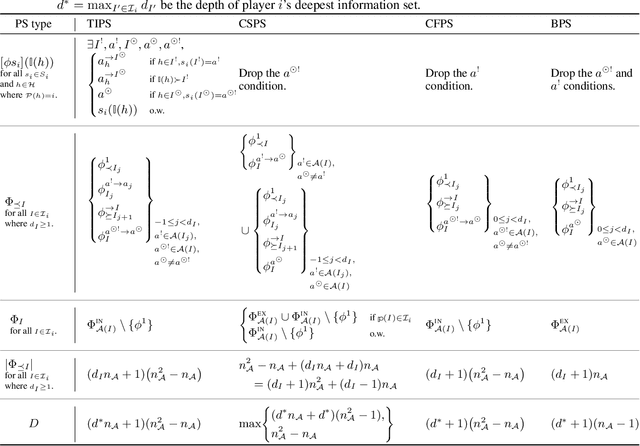
Hindsight rationality is an approach to playing multi-agent, general-sum games that prescribes no-regret learning dynamics and describes jointly rational behavior with mediated equilibria. We explore the space of deviation types in extensive-form games (EFGs) and discover powerful types that are efficient to compute in games with moderate lengths. Specifically, we identify four new types of deviations that subsume previously studied types within a broader class we call partial sequence deviations. Integrating the idea of time selection regret minimization into counterfactual regret minimization (CFR), we introduce the extensive-form regret minimization (EFR) algorithm that is hindsight rational for a general and natural class of deviations in EFGs. We provide instantiations and regret bounds for EFR that correspond to each partial sequence deviation type. In addition, we present a thorough empirical analysis of EFR's performance with different deviation types in common benchmark games. As theory suggests, instantiating EFR with stronger deviations leads to behavior that tends to outperform that of weaker deviations.

Optimistic and Adaptive Lagrangian Hedging

In online learning an algorithm plays against an environment with losses possibly picked by an adversary at each round. The generality of this framework includes problems that are not adversarial, for example offline optimization, or saddle point problems (i.e. min max optimization). However, online algorithms are typically not designed to leverage additional structure present in non-adversarial problems. Recently, slight modifications to well-known online algorithms such as optimism and adaptive step sizes have been used in several domains to accelerate online learning -- recovering optimal rates in offline smooth optimization, and accelerating convergence to saddle points or social welfare in smooth games. In this work we introduce optimism and adaptive stepsizes to Lagrangian hedging, a class of online algorithms that includes regret-matching, and hedge (i.e. multiplicative weights). Our results include: a general general regret bound; a path length regret bound for a fixed smooth loss, applicable to an optimistic variant of regret-matching and regret-matching+; optimistic regret bounds for $\Phi$ regret, a framework that includes external, internal, and swap regret; and optimistic bounds for a family of algorithms that includes regret-matching+ as a special case.

Solving Common-Payoff Games with Approximate Policy Iteration

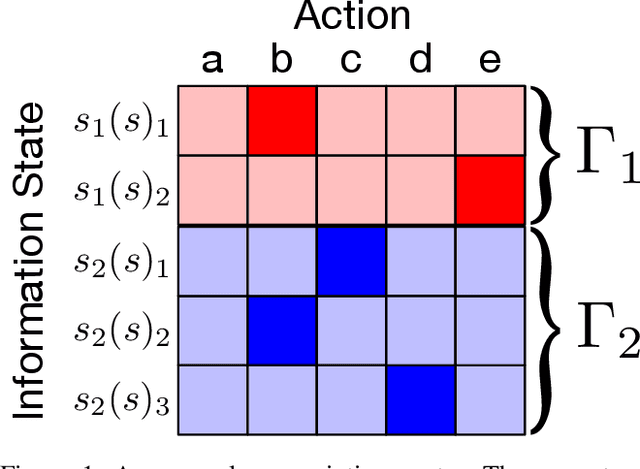
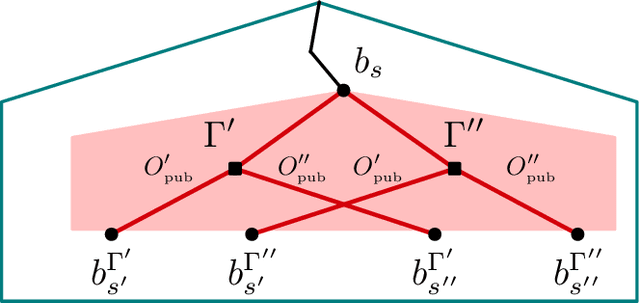
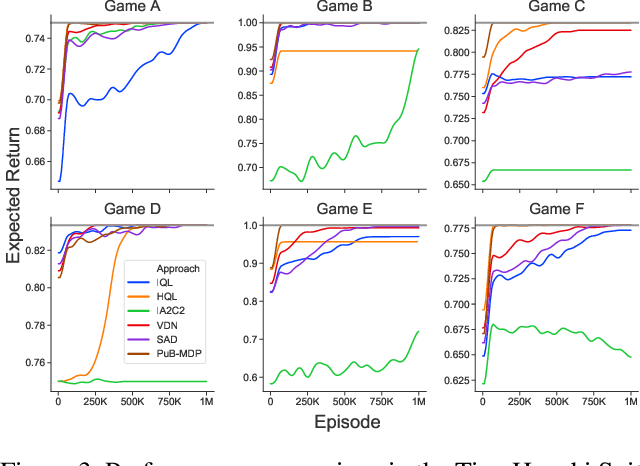
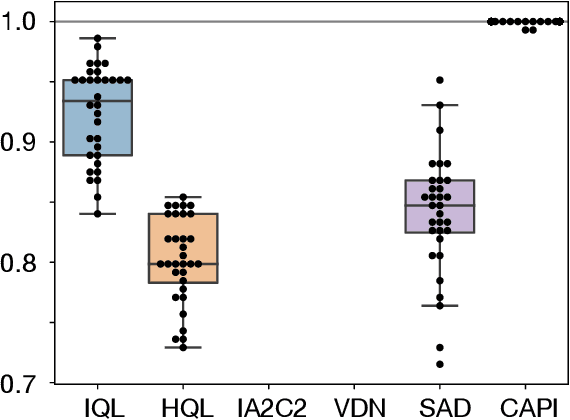
For artificially intelligent learning systems to have widespread applicability in real-world settings, it is important that they be able to operate decentrally. Unfortunately, decentralized control is difficult -- computing even an epsilon-optimal joint policy is a NEXP complete problem. Nevertheless, a recently rediscovered insight -- that a team of agents can coordinate via common knowledge -- has given rise to algorithms capable of finding optimal joint policies in small common-payoff games. The Bayesian action decoder (BAD) leverages this insight and deep reinforcement learning to scale to games as large as two-player Hanabi. However, the approximations it uses to do so prevent it from discovering optimal joint policies even in games small enough to brute force optimal solutions. This work proposes CAPI, a novel algorithm which, like BAD, combines common knowledge with deep reinforcement learning. However, unlike BAD, CAPI prioritizes the propensity to discover optimal joint policies over scalability. While this choice precludes CAPI from scaling to games as large as Hanabi, empirical results demonstrate that, on the games to which CAPI does scale, it is capable of discovering optimal joint policies even when other modern multi-agent reinforcement learning algorithms are unable to do so. Code is available at https://github.com/ssokota/capi .

Hindsight and Sequential Rationality of Correlated Play

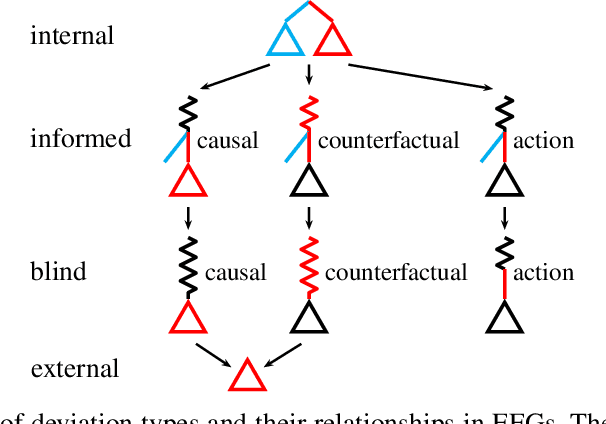
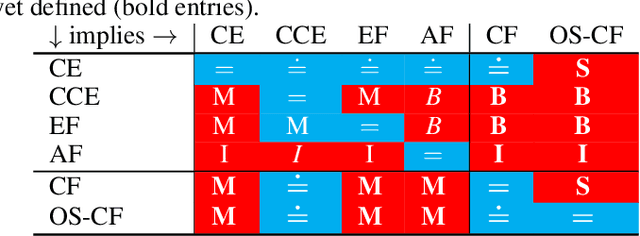
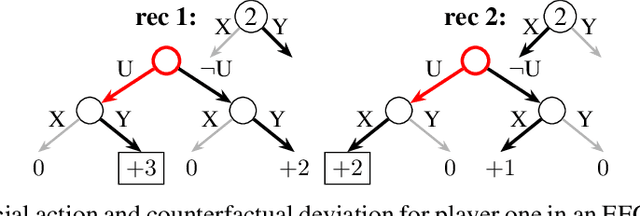
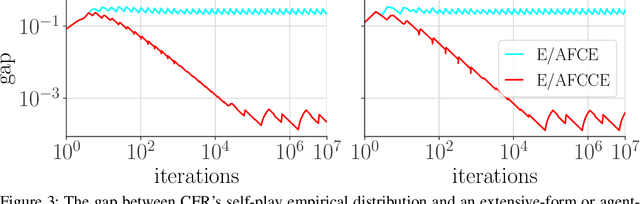
Driven by recent successes in two-player, zero-sum game solving and playing, artificial intelligence work on games has increasingly focused on algorithms that produce equilibrium-based strategies. However, this approach has been less effective at producing competent players in general-sum games or those with more than two players than in two-player, zero-sum games. An appealing alternative is to consider adaptive algorithms that ensure strong performance in hindsight relative to what could have been achieved with modified behavior. This approach also leads to a game-theoretic analysis, but in the correlated play that arises from joint learning dynamics rather than factored agent behavior at equilibrium. We develop and advocate for this hindsight rationality framing of learning in general sequential decision-making settings. To this end, we re-examine mediated equilibrium and deviation types in extensive-form games, thereby gaining a more complete understanding and resolving past misconceptions. We present a set of examples illustrating the distinct strengths and weaknesses of each type of equilibrium in the literature, and prove that no tractable concept subsumes all others. This line of inquiry culminates in the definition of the deviation and equilibrium classes that correspond to algorithms in the counterfactual regret minimization (CFR) family, relating them to all others in the literature. Examining CFR in greater detail further leads to a new recursive definition of rationality in correlated play that extends sequential rationality in a way that naturally applies to hindsight evaluation.

Alternative Function Approximation Parameterizations for Solving Games: An Analysis of $f$-Regression Counterfactual Regret Minimization

Function approximation is a powerful approach for structuring large decision problems that has facilitated great achievements in the areas of reinforcement learning and game playing. Regression counterfactual regret minimization (RCFR) is a flexible and simple algorithm for approximately solving imperfect information games with policies parameterized by a normalized rectified linear unit (ReLU). In contrast, the more conventional softmax parameterization is standard in the field of reinforcement learning and has a regret bound with a better dependence on the number of actions in the tabular case. We derive approximation error-aware regret bounds for $(\Phi, f)$-regret matching, which applies to a general class of link functions and regret objectives. These bounds recover a tighter bound for RCFR and provides a theoretical justification for RCFR implementations with alternative policy parameterizations ($f$-RCFR), including softmax. We provide exploitability bounds for $f$-RCFR with the polynomial and exponential link functions in zero-sum imperfect information games, and examine empirically how the link function interacts with the severity of the approximation to determine exploitability performance in practice. Although a ReLU parameterized policy is typically the best choice, a softmax parameterization can perform as well or better in settings that require aggressive approximation.