Composing Efficient, Robust Tests for Policy Selection

Modern reinforcement learning systems produce many high-quality policies throughout the learning process. However, to choose which policy to actually deploy in the real world, they must be tested under an intractable number of environmental conditions. We introduce RPOSST, an algorithm to select a small set of test cases from a larger pool based on a relatively small number of sample evaluations. RPOSST treats the test case selection problem as a two-player game and optimizes a solution with provable $k$-of-$N$ robustness, bounding the error relative to a test that used all the test cases in the pool. Empirical results demonstrate that RPOSST finds a small set of test cases that identify high quality policies in a toy one-shot game, poker datasets, and a high-fidelity racing simulator.

Interpolating Between Softmax Policy Gradient and Neural Replicator Dynamics with Capped Implicit Exploration

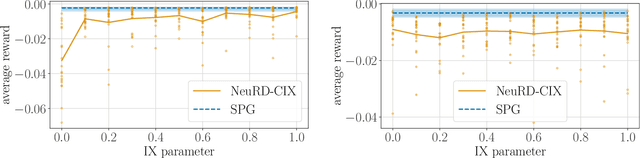
Neural replicator dynamics (NeuRD) is an alternative to the foundational softmax policy gradient (SPG) algorithm motivated by online learning and evolutionary game theory. The NeuRD expected update is designed to be nearly identical to that of SPG, however, we show that the Monte Carlo updates differ in a substantial way: the importance correction accounting for a sampled action is nullified in the SPG update, but not in the NeuRD update. Naturally, this causes the NeuRD update to have higher variance than its SPG counterpart. Building on implicit exploration algorithms in the adversarial bandit setting, we introduce capped implicit exploration (CIX) estimates that allow us to construct NeuRD-CIX, which interpolates between this aspect of NeuRD and SPG. We show how CIX estimates can be used in a black-box reduction to construct bandit algorithms with regret bounds that hold with high probability and the benefits this entails for NeuRD-CIX in sequential decision-making settings. Our analysis reveals a bias--variance tradeoff between SPG and NeuRD, and shows how theory predicts that NeuRD-CIX will perform well more consistently than NeuRD while retaining NeuRD's advantages over SPG in non-stationary environments.

Efficient Deviation Types and Learning for Hindsight Rationality in Extensive-Form Games: Corrections

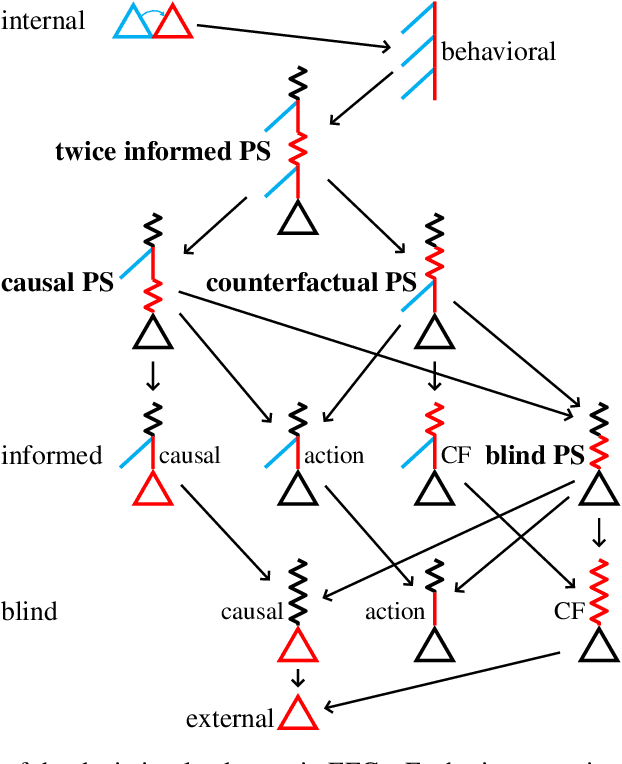
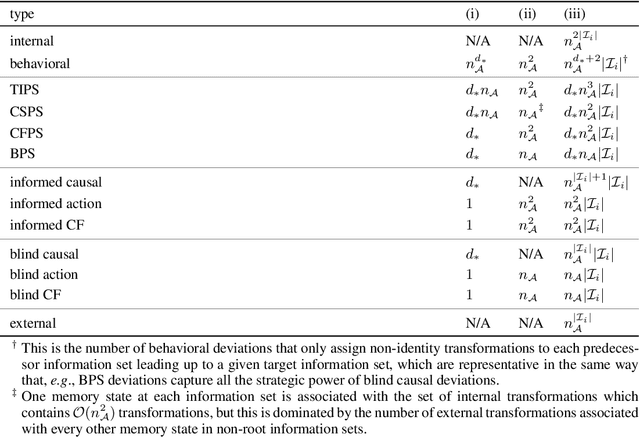
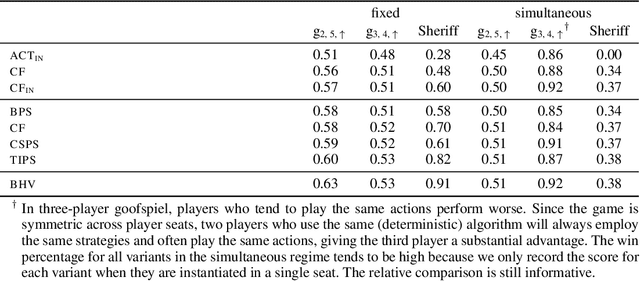
Hindsight rationality is an approach to playing general-sum games that prescribes no-regret learning dynamics for individual agents with respect to a set of deviations, and further describes jointly rational behavior among multiple agents with mediated equilibria. To develop hindsight rational learning in sequential decision-making settings, we formalize behavioral deviations as a general class of deviations that respect the structure of extensive-form games. Integrating the idea of time selection into counterfactual regret minimization (CFR), we introduce the extensive-form regret minimization (EFR) algorithm that achieves hindsight rationality for any given set of behavioral deviations with computation that scales closely with the complexity of the set. We identify behavioral deviation subsets, the partial sequence deviation types, that subsume previously studied types and lead to efficient EFR instances in games with moderate lengths. In addition, we present a thorough empirical analysis of EFR instantiated with different deviation types in benchmark games, where we find that stronger types typically induce better performance.

The Partially Observable History Process

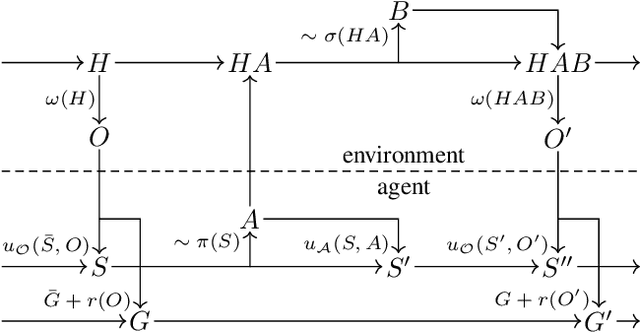
We introduce the partially observable history process (POHP) formalism for reinforcement learning. POHP centers around the actions and observations of a single agent and abstracts away the presence of other players without reducing them to stochastic processes. Our formalism provides a streamlined interface for designing algorithms that defy categorization as exclusively single or multi-agent, and for developing theory that applies across these domains. We show how the POHP formalism unifies traditional models including the Markov decision process, the Markov game, the extensive-form game, and their partially observable extensions, without introducing burdensome technical machinery or violating the philosophical underpinnings of reinforcement learning. We illustrate the utility of our formalism by concisely exploring observable sequential rationality, re-deriving the extensive-form regret minimization (EFR) algorithm, and examining EFR's theoretical properties in greater generality.

Learning to Be Cautious

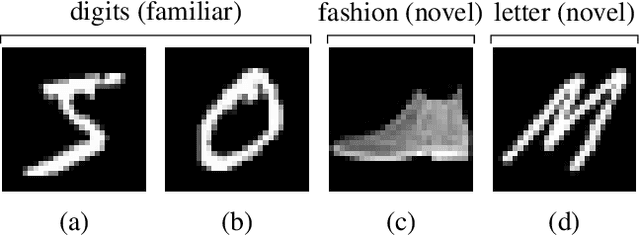
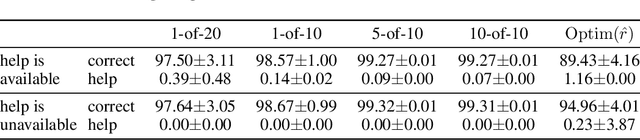
A key challenge in the field of reinforcement learning is to develop agents that behave cautiously in novel situations. It is generally impossible to anticipate all situations that an autonomous system may face or what behavior would best avoid bad outcomes. An agent that could learn to be cautious would overcome this challenge by discovering for itself when and how to behave cautiously. In contrast, current approaches typically embed task-specific safety information or explicit cautious behaviors into the system, which is error-prone and imposes extra burdens on practitioners. In this paper, we present both a sequence of tasks where cautious behavior becomes increasingly non-obvious, as well as an algorithm to demonstrate that it is possible for a system to \emph{learn} to be cautious. The essential features of our algorithm are that it characterizes reward function uncertainty without task-specific safety information and uses this uncertainty to construct a robust policy. Specifically, we construct robust policies with a $k$-of-$N$ counterfactual regret minimization (CFR) subroutine given a learned reward function uncertainty represented by a neural network ensemble belief. These policies exhibit caution in each of our tasks without any task-specific safety tuning.

Efficient Deviation Types and Learning for Hindsight Rationality in Extensive-Form Games

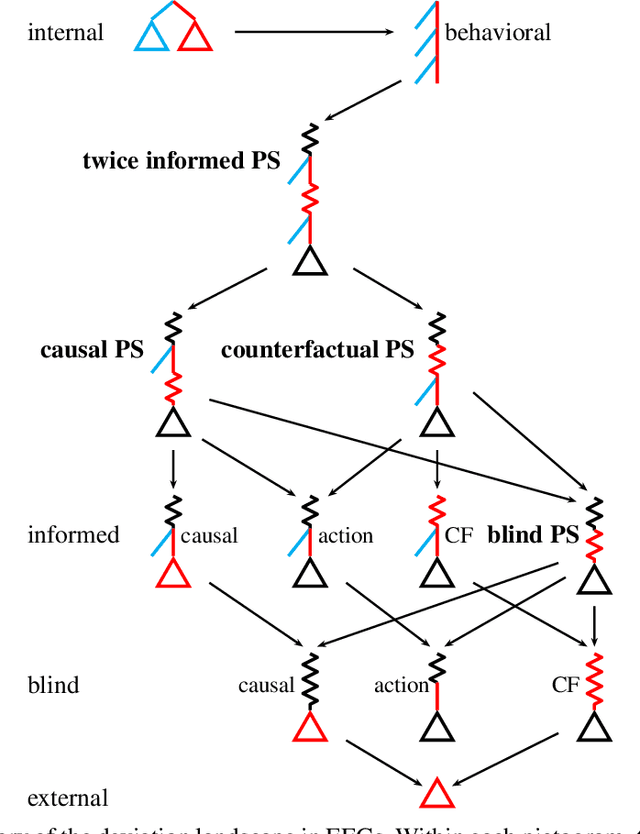
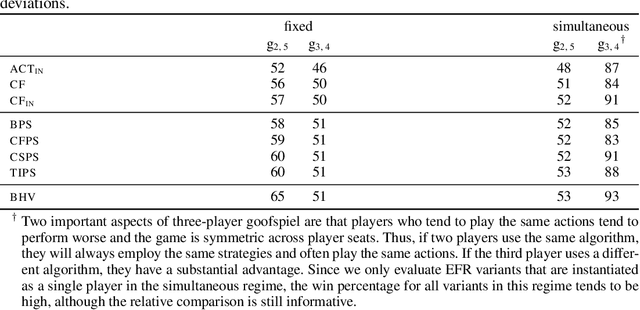
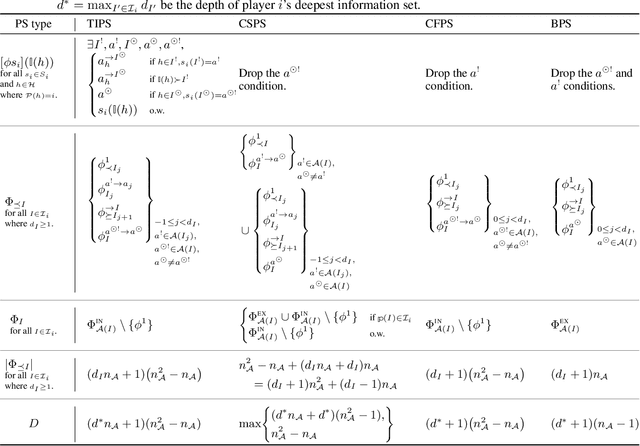
Hindsight rationality is an approach to playing multi-agent, general-sum games that prescribes no-regret learning dynamics and describes jointly rational behavior with mediated equilibria. We explore the space of deviation types in extensive-form games (EFGs) and discover powerful types that are efficient to compute in games with moderate lengths. Specifically, we identify four new types of deviations that subsume previously studied types within a broader class we call partial sequence deviations. Integrating the idea of time selection regret minimization into counterfactual regret minimization (CFR), we introduce the extensive-form regret minimization (EFR) algorithm that is hindsight rational for a general and natural class of deviations in EFGs. We provide instantiations and regret bounds for EFR that correspond to each partial sequence deviation type. In addition, we present a thorough empirical analysis of EFR's performance with different deviation types in common benchmark games. As theory suggests, instantiating EFR with stronger deviations leads to behavior that tends to outperform that of weaker deviations.

Hindsight and Sequential Rationality of Correlated Play

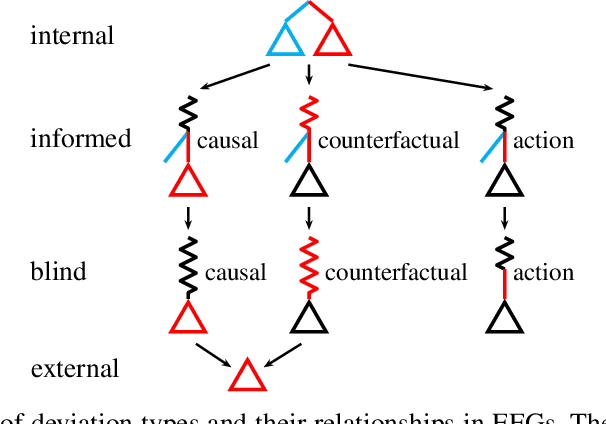
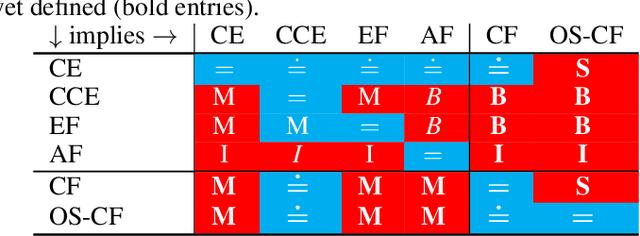
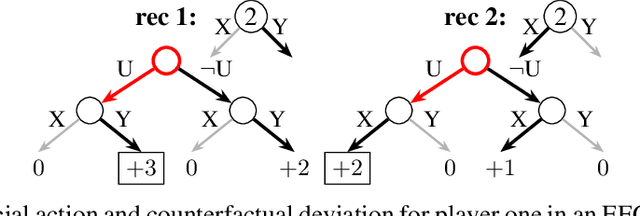
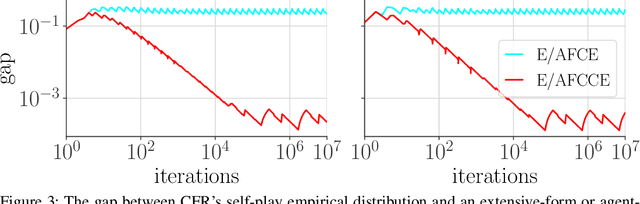
Driven by recent successes in two-player, zero-sum game solving and playing, artificial intelligence work on games has increasingly focused on algorithms that produce equilibrium-based strategies. However, this approach has been less effective at producing competent players in general-sum games or those with more than two players than in two-player, zero-sum games. An appealing alternative is to consider adaptive algorithms that ensure strong performance in hindsight relative to what could have been achieved with modified behavior. This approach also leads to a game-theoretic analysis, but in the correlated play that arises from joint learning dynamics rather than factored agent behavior at equilibrium. We develop and advocate for this hindsight rationality framing of learning in general sequential decision-making settings. To this end, we re-examine mediated equilibrium and deviation types in extensive-form games, thereby gaining a more complete understanding and resolving past misconceptions. We present a set of examples illustrating the distinct strengths and weaknesses of each type of equilibrium in the literature, and prove that no tractable concept subsumes all others. This line of inquiry culminates in the definition of the deviation and equilibrium classes that correspond to algorithms in the counterfactual regret minimization (CFR) family, relating them to all others in the literature. Examining CFR in greater detail further leads to a new recursive definition of rationality in correlated play that extends sequential rationality in a way that naturally applies to hindsight evaluation.

The Advantage Regret-Matching Actor-Critic

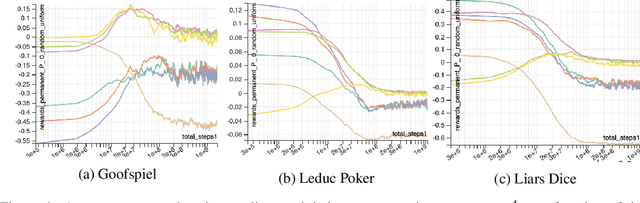
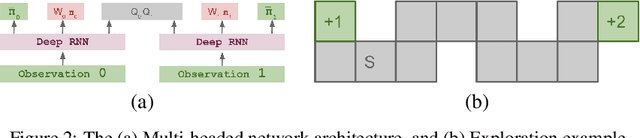
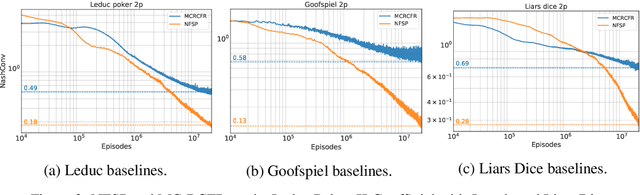
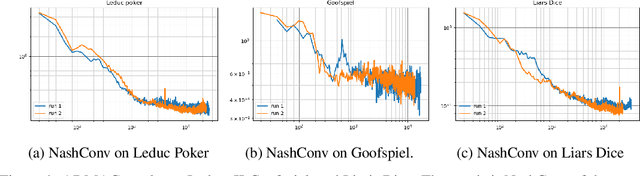
Regret minimization has played a key role in online learning, equilibrium computation in games, and reinforcement learning (RL). In this paper, we describe a general model-free RL method for no-regret learning based on repeated reconsideration of past behavior. We propose a model-free RL algorithm, the AdvantageRegret-Matching Actor-Critic (ARMAC): rather than saving past state-action data, ARMAC saves a buffer of past policies, replaying through them to reconstruct hindsight assessments of past behavior. These retrospective value estimates are used to predict conditional advantages which, combined with regret matching, produces a new policy. In particular, ARMAC learns from sampled trajectories in a centralized training setting, without requiring the application of importance sampling commonly used in Monte Carlo counterfactual regret (CFR) minimization; hence, it does not suffer from excessive variance in large environments. In the single-agent setting, ARMAC shows an interesting form of exploration by keeping past policies intact. In the multiagent setting, ARMAC in self-play approaches Nash equilibria on some partially-observable zero-sum benchmarks. We provide exploitability estimates in the significantly larger game of betting-abstracted no-limit Texas Hold'em.

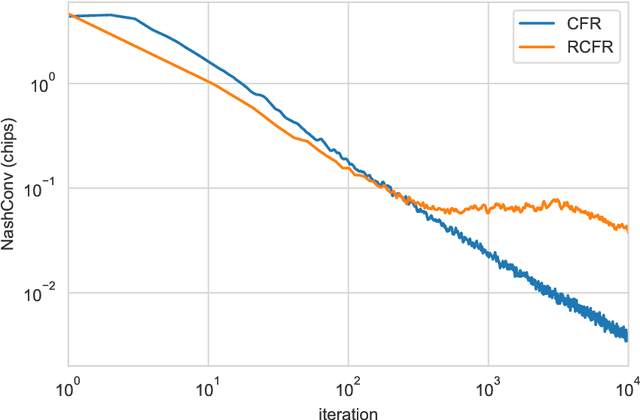
Alternative Function Approximation Parameterizations for Solving Games: An Analysis of $f$-Regression Counterfactual Regret Minimization

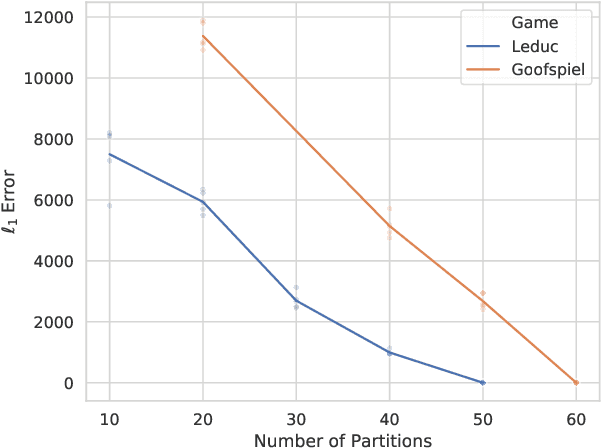
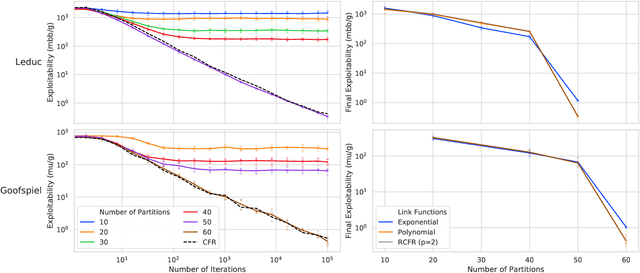
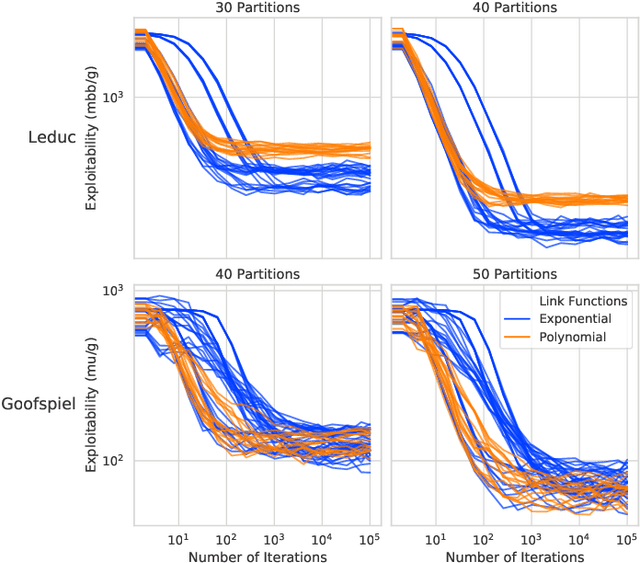
Function approximation is a powerful approach for structuring large decision problems that has facilitated great achievements in the areas of reinforcement learning and game playing. Regression counterfactual regret minimization (RCFR) is a flexible and simple algorithm for approximately solving imperfect information games with policies parameterized by a normalized rectified linear unit (ReLU). In contrast, the more conventional softmax parameterization is standard in the field of reinforcement learning and has a regret bound with a better dependence on the number of actions in the tabular case. We derive approximation error-aware regret bounds for $(\Phi, f)$-regret matching, which applies to a general class of link functions and regret objectives. These bounds recover a tighter bound for RCFR and provides a theoretical justification for RCFR implementations with alternative policy parameterizations ($f$-RCFR), including softmax. We provide exploitability bounds for $f$-RCFR with the polynomial and exponential link functions in zero-sum imperfect information games, and examine empirically how the link function interacts with the severity of the approximation to determine exploitability performance in practice. Although a ReLU parameterized policy is typically the best choice, a softmax parameterization can perform as well or better in settings that require aggressive approximation.

OpenSpiel: A Framework for Reinforcement Learning in Games

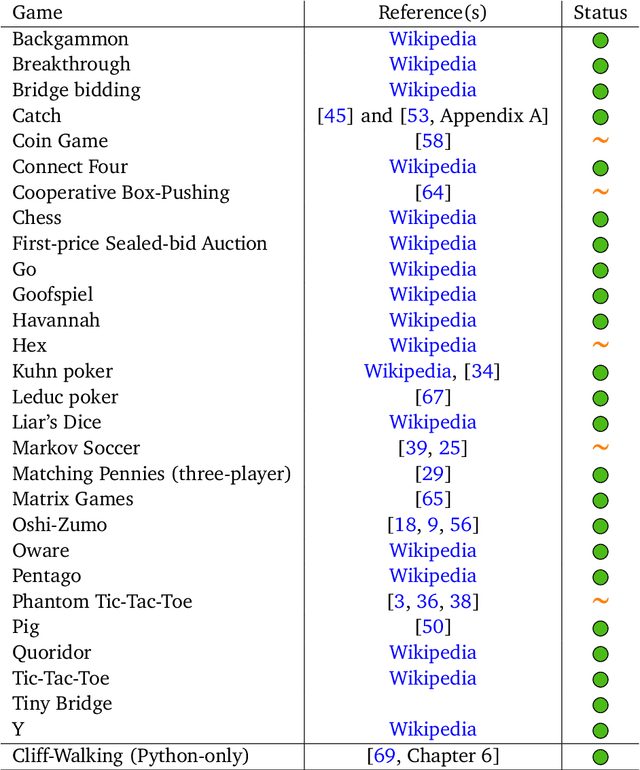
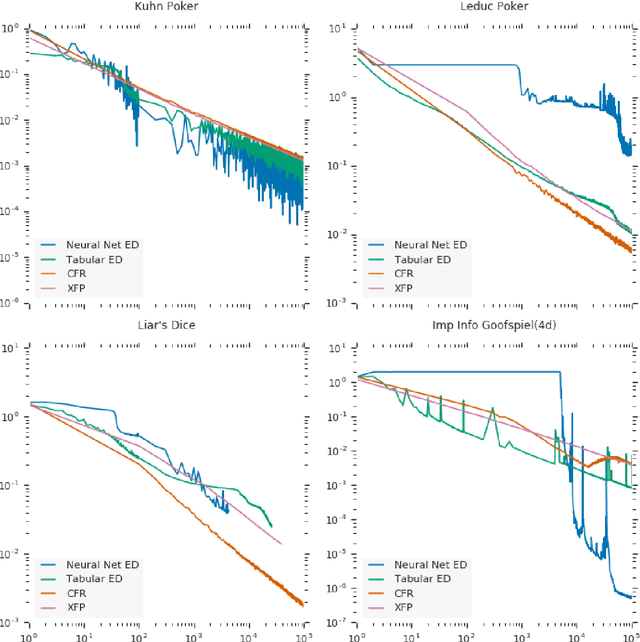
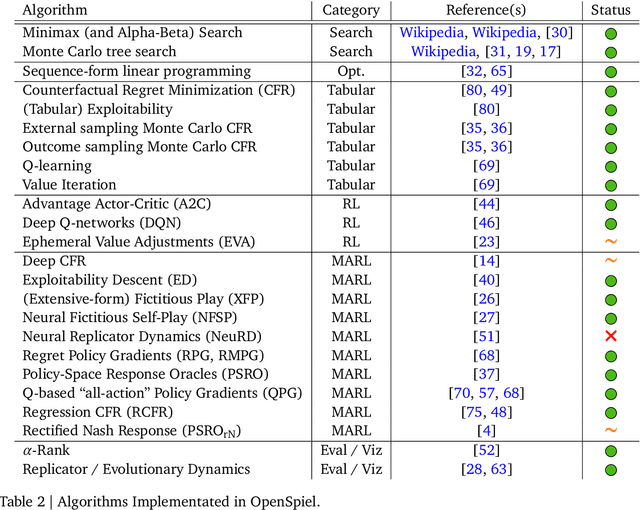
OpenSpiel is a collection of environments and algorithms for research in general reinforcement learning and search/planning in games. OpenSpiel supports n-player (single- and multi- agent) zero-sum, cooperative and general-sum, one-shot and sequential, strictly turn-taking and simultaneous-move, perfect and imperfect information games, as well as traditional multiagent environments such as (partially- and fully- observable) grid worlds and social dilemmas. OpenSpiel also includes tools to analyze learning dynamics and other common evaluation metrics. This document serves both as an overview of the code base and an introduction to the terminology, core concepts, and algorithms across the fields of reinforcement learning, computational game theory, and search.