On the Optimality of Dilated Entropy and Lower Bounds for Online Learning in Extensive-Form Games

First-order methods (FOMs) are arguably the most scalable algorithms for equilibrium computation in large extensive-form games. To operationalize these methods, a distance-generating function, acting as a regularizer for the strategy space, must be chosen. The ratio between the strong convexity modulus and the diameter of the regularizer is a key parameter in the analysis of FOMs. A natural question is then: what is the optimal distance-generating function for extensive-form decision spaces? In this paper, we make a number of contributions, ultimately establishing that the weight-one dilated entropy (DilEnt) distance-generating function is optimal up to logarithmic factors. The DilEnt regularizer is notable due to its iterate-equivalence with Kernelized OMWU (KOMWU) -- the algorithm with state-of-the-art dependence on the game tree size in extensive-form games -- when used in conjunction with the online mirror descent (OMD) algorithm. However, the standard analysis for OMD is unable to establish such a result; the only current analysis is by appealing to the iterate equivalence to KOMWU. We close this gap by introducing a pair of primal-dual treeplex norms, which we contend form the natural analytic viewpoint for studying the strong convexity of DilEnt. Using these norm pairs, we recover the diameter-to-strong-convexity ratio that predicts the same performance as KOMWU. Along with a new regret lower bound for online learning in sequence-form strategy spaces, we show that this ratio is nearly optimal. Finally, we showcase our analytic techniques by refining the analysis of Clairvoyant OMD when paired with DilEnt, establishing an $\mathcal{O}(n \log |\mathcal{V}| \log T/T)$ approximation rate to coarse correlated equilibrium in $n$-player games, where $|\mathcal{V}|$ is the number of reduced normal-form strategies of the players, establishing the new state of the art.

Fast Last-Iterate Convergence of Learning in Games Requires Forgetful Algorithms

Self-play via online learning is one of the premier ways to solve large-scale two-player zero-sum games, both in theory and practice. Particularly popular algorithms include optimistic multiplicative weights update (OMWU) and optimistic gradient-descent-ascent (OGDA). While both algorithms enjoy $O(1/T)$ ergodic convergence to Nash equilibrium in two-player zero-sum games, OMWU offers several advantages including logarithmic dependence on the size of the payoff matrix and $\widetilde{O}(1/T)$ convergence to coarse correlated equilibria even in general-sum games. However, in terms of last-iterate convergence in two-player zero-sum games, an increasingly popular topic in this area, OGDA guarantees that the duality gap shrinks at a rate of $O(1/\sqrt{T})$, while the best existing last-iterate convergence for OMWU depends on some game-dependent constant that could be arbitrarily large. This begs the question: is this potentially slow last-iterate convergence an inherent disadvantage of OMWU, or is the current analysis too loose? Somewhat surprisingly, we show that the former is true. More generally, we prove that a broad class of algorithms that do not forget the past quickly all suffer the same issue: for any arbitrarily small $\delta>0$, there exists a $2\times 2$ matrix game such that the algorithm admits a constant duality gap even after $1/\delta$ rounds. This class of algorithms includes OMWU and other standard optimistic follow-the-regularized-leader algorithms.

Last-Iterate Convergence Properties of Regret-Matching Algorithms in Games

Algorithms based on regret matching, specifically regret matching$^+$ (RM$^+$), and its variants are the most popular approaches for solving large-scale two-player zero-sum games in practice. Unlike algorithms such as optimistic gradient descent ascent, which have strong last-iterate and ergodic convergence properties for zero-sum games, virtually nothing is known about the last-iterate properties of regret-matching algorithms. Given the importance of last-iterate convergence for numerical optimization reasons and relevance as modeling real-word learning in games, in this paper, we study the last-iterate convergence properties of various popular variants of RM$^+$. First, we show numerically that several practical variants such as simultaneous RM$^+$, alternating RM$^+$, and simultaneous predictive RM$^+$, all lack last-iterate convergence guarantees even on a simple $3\times 3$ game. We then prove that recent variants of these algorithms based on a smoothing technique do enjoy last-iterate convergence: we prove that extragradient RM$^{+}$ and smooth Predictive RM$^+$ enjoy asymptotic last-iterate convergence (without a rate) and $1/\sqrt{t}$ best-iterate convergence. Finally, we introduce restarted variants of these algorithms, and show that they enjoy linear-rate last-iterate convergence.

Regret Matching+: (In)Stability and Fast Convergence in Games

Regret Matching+ (RM+) and its variants are important algorithms for solving large-scale games. However, a theoretical understanding of their success in practice is still a mystery. Moreover, recent advances on fast convergence in games are limited to no-regret algorithms such as online mirror descent, which satisfy stability. In this paper, we first give counterexamples showing that RM+ and its predictive version can be unstable, which might cause other players to suffer large regret. We then provide two fixes: restarting and chopping off the positive orthant that RM+ works in. We show that these fixes are sufficient to get $O(T^{1/4})$ individual regret and $O(1)$ social regret in normal-form games via RM+ with predictions. We also apply our stabilizing techniques to clairvoyant updates in the uncoupled learning setting for RM+ and prove desirable results akin to recent works for Clairvoyant online mirror descent. Our experiments show the advantages of our algorithms over vanilla RM+-based algorithms in matrix and extensive-form games.

Online Bidding in Repeated Non-Truthful Auctions under Budget and ROI Constraints

Online advertising platforms typically use auction mechanisms to allocate ad placements. Advertisers participate in a series of repeated auctions, and must select bids that will maximize their overall rewards while adhering to certain constraints. We focus on the scenario in which the advertiser has budget and return-on-investment (ROI) constraints. We investigate the problem of budget- and ROI-constrained bidding in repeated non-truthful auctions, such as first-price auctions, and present a best-of-both-worlds framework with no-regret guarantees under both stochastic and adversarial inputs. By utilizing the notion of interval regret, we demonstrate that our framework does not require knowledge of specific parameters of the problem which could be difficult to determine in practice. Our proof techniques can be applied to both the adversarial and stochastic cases with minimal modifications, thereby providing a unified perspective on the two problems. In the adversarial setting, we also show that it is possible to loosen the traditional requirement of having a strictly feasible solution to the offline optimization problem at each round.

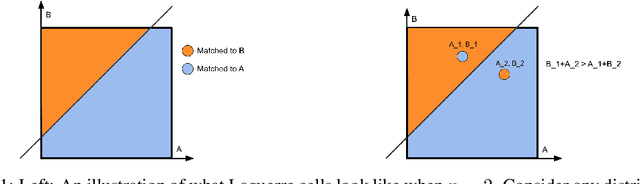
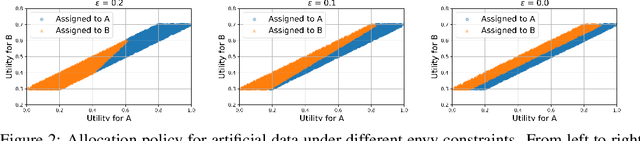
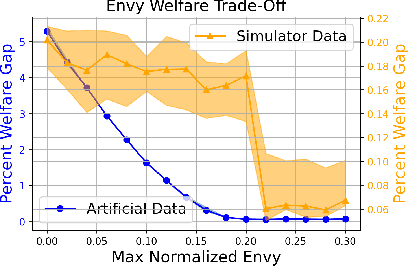
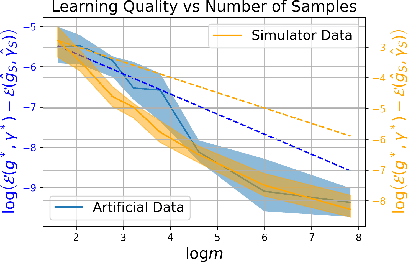
Optimal Efficiency-Envy Trade-Off via Optimal Transport

We consider the problem of allocating a distribution of items to $n$ recipients where each recipient has to be allocated a fixed, prespecified fraction of all items, while ensuring that each recipient does not experience too much envy. We show that this problem can be formulated as a variant of the semi-discrete optimal transport (OT) problem, whose solution structure in this case has a concise representation and a simple geometric interpretation. Unlike existing literature that treats envy-freeness as a hard constraint, our formulation allows us to \emph{optimally} trade off efficiency and envy continuously. Additionally, we study the statistical properties of the space of our OT based allocation policies by showing a polynomial bound on the number of samples needed to approximate the optimal solution from samples. Our approach is suitable for large-scale fair allocation problems such as the blood donation matching problem, and we show numerically that it performs well on a prior realistic data simulator.

Computing the optimal distributionally-robust strategy to commit to

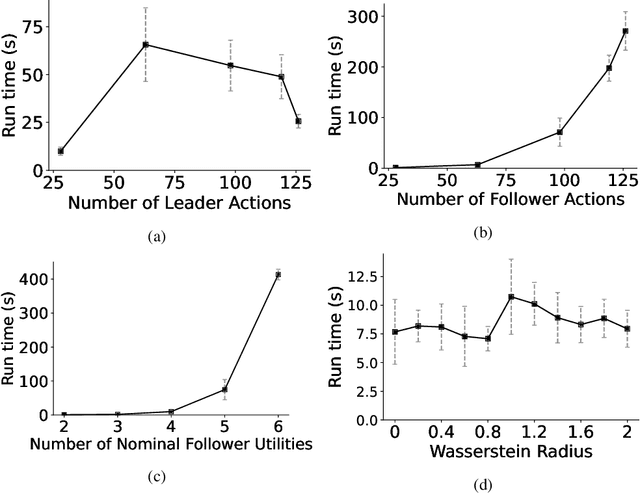
The Stackelberg game model, where a leader commits to a strategy and the follower best responds, has found widespread application, particularly to security problems. In the security setting, the goal is for the leader to compute an optimal strategy to commit to, in order to protect some asset. In many of these applications, the parameters of the follower utility model are not known with certainty. Distributionally-robust optimization addresses this issue by allowing a distribution over possible model parameters, where this distribution comes from a set of possible distributions. The goal is to maximize the expected utility with respect to the worst-case distribution. We initiate the study of distributionally-robust models for computing the optimal strategy to commit to. We consider the case of normal-form games with uncertainty about the follower utility model. Our main theoretical result is to show that a distributionally-robust Stackelberg equilibrium always exists across a wide array of uncertainty models. For the case of a finite set of possible follower utility functions we present two algorithms to compute a distributionally-robust strong Stackelberg equilibrium (DRSSE) using mathematical programs. Next, in the general case where there is an infinite number of possible follower utility functions and the uncertainty is represented by a Wasserstein ball around a finitely-supported nominal distribution, we give an incremental mixed-integer-programming-based algorithm for computing the optimal distributionally-robust strategy. Experiments substantiate the tractability of our algorithm on a classical Stackelberg game, showing that our approach scales to medium-sized games.

Online Resource Allocation under Horizon Uncertainty

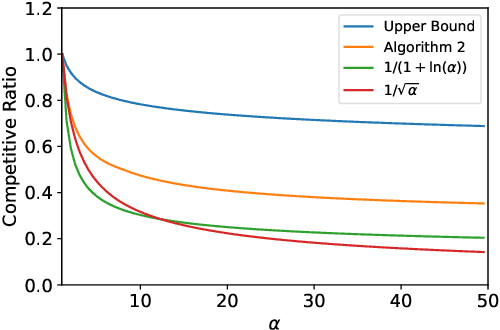
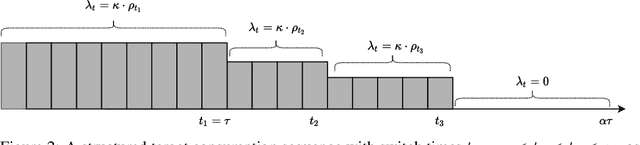
We study stochastic online resource allocation: a decision maker needs to allocate limited resources to stochastically-generated sequentially-arriving requests in order to maximize reward. Motivated by practice, we consider a data-driven setting in which requests are drawn independently from a distribution that is unknown to the decision maker. Online resource allocation and its special cases have been studied extensively in the past, but these previous results crucially and universally rely on a practically-untenable assumption: the total number of requests (the horizon) is known to the decision maker in advance. In many applications, such as revenue management and online advertising, the number of requests can vary widely because of fluctuations in demand or user traffic intensity. In this work, we develop online algorithms that are robust to horizon uncertainty. In sharp contrast to the known-horizon setting, we show that no algorithm can achieve a constant asymptotic competitive ratio that is independent of the horizon uncertainty. We then introduce a novel algorithm that combines dual mirror descent with a carefully-chosen target consumption sequence and prove that it achieves a bounded competitive ratio. Our algorithm is near-optimal in the sense that its competitive ratio attains the optimal rate of growth when the horizon uncertainty grows large.

Near-Optimal No-Regret Learning for General Convex Games

A recent line of work has established uncoupled learning dynamics such that, when employed by all players in a game, each player's \emph{regret} after $T$ repetitions grows polylogarithmically in $T$, an exponential improvement over the traditional guarantees within the no-regret framework. However, so far these results have only been limited to certain classes of games with structured strategy spaces -- such as normal-form and extensive-form games. The question as to whether $O(\text{polylog} T)$ regret bounds can be obtained for general convex and compact strategy sets -- which occur in many fundamental models in economics and multiagent systems -- while retaining efficient strategy updates is an important question. In this paper, we answer this in the positive by establishing the first uncoupled learning algorithm with $O(\log T)$ per-player regret in general \emph{convex games}, that is, games with concave utility functions supported on arbitrary convex and compact strategy sets. Our learning dynamics are based on an instantiation of optimistic follow-the-regularized-leader over an appropriately \emph{lifted} space using a \emph{self-concordant regularizer} that is, peculiarly, not a barrier for the feasible region. Further, our learning dynamics are efficiently implementable given access to a proximal oracle for the convex strategy set, leading to $O(\log\log T)$ per-iteration complexity; we also give extensions when access to only a \emph{linear} optimization oracle is assumed. Finally, we adapt our dynamics to guarantee $O(\sqrt{T})$ regret in the adversarial regime. Even in those special cases where prior results apply, our algorithm improves over the state-of-the-art regret bounds either in terms of the dependence on the number of iterations or on the dimension of the strategy sets.

A Unified Approach to Reinforcement Learning, Quantal Response Equilibria, and Two-Player Zero-Sum Games

Algorithms designed for single-agent reinforcement learning (RL) generally fail to converge to equilibria in two-player zero-sum (2p0s) games. Conversely, game-theoretic algorithms for approximating Nash and quantal response equilibria (QREs) in 2p0s games are not typically competitive for RL and can be difficult to scale. As a result, algorithms for these two cases are generally developed and evaluated separately. In this work, we show that a single algorithm -- a simple extension to mirror descent with proximal regularization that we call magnetic mirror descent (MMD) -- can produce strong results in both settings, despite their fundamental differences. From a theoretical standpoint, we prove that MMD converges linearly to QREs in extensive-form games -- this is the first time linear convergence has been proven for a first order solver. Moreover, applied as a tabular Nash equilibrium solver via self-play, we show empirically that MMD produces results competitive with CFR in both normal-form and extensive-form games with full feedback (this is the first time that a standard RL algorithm has done so) and also that MMD empirically converges in black-box feedback settings. Furthermore, for single-agent deep RL, on a small collection of Atari and Mujoco games, we show that MMD can produce results competitive with those of PPO. Lastly, for multi-agent deep RL, we show MMD can outperform NFSP in 3x3 Abrupt Dark Hex.