Reducing Selection Bias in Counterfactual Reasoning for Individual Treatment Effects Estimation

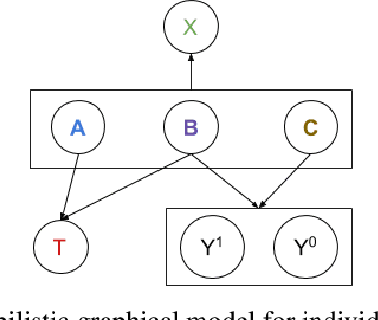
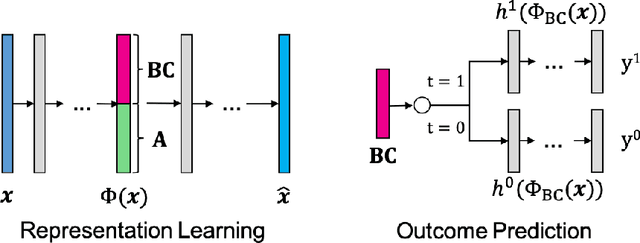
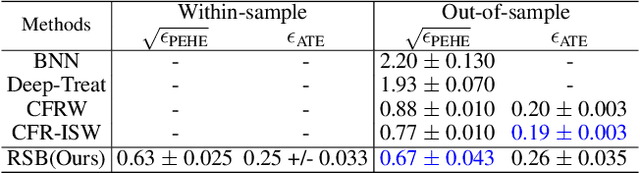
Counterfactual reasoning is an important paradigm applicable in many fields, such as healthcare, economics, and education. In this work, we propose a novel method to address the issue of \textit{selection bias}. We learn two groups of latent random variables, where one group corresponds to variables that only cause selection bias, and the other group is relevant for outcome prediction. They are learned by an auto-encoder where an additional regularized loss based on Pearson Correlation Coefficient (PCC) encourages the de-correlation between the two groups of random variables. This allows for explicitly alleviating selection bias by only keeping the latent variables that are relevant for estimating individual treatment effects. Experimental results on a synthetic toy dataset and a benchmark dataset show that our algorithm is able to achieve state-of-the-art performance and improve the result of its counterpart that does not explicitly model the selection bias.

Domain Aggregation Networks for Multi-Source Domain Adaptation

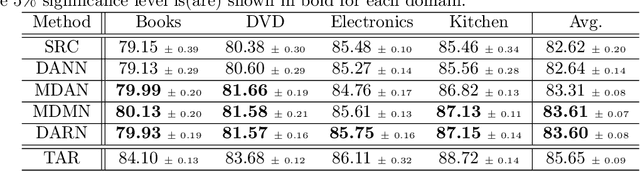
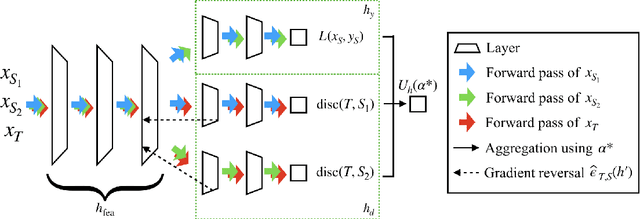
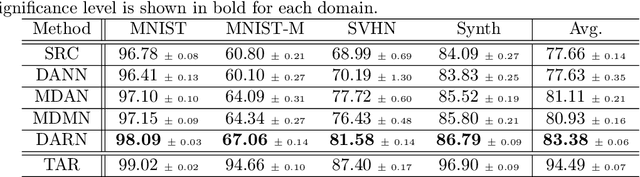
In many real-world applications, we want to exploit multiple source datasets of similar tasks to learn a model for a different but related target dataset -- e.g., recognizing characters of a new font using a set of different fonts. While most recent research has considered ad-hoc combination rules to address this problem, we extend previous work on domain discrepancy minimization to develop a finite-sample generalization bound, and accordingly propose a theoretically justified optimization procedure. The algorithm we develop, Domain AggRegation Network (DARN), is able to effectively adjust the weight of each source domain during training to ensure relevant domains are given more importance for adaptation. We evaluate the proposed method on real-world sentiment analysis and digit recognition datasets and show that DARN can significantly outperform the state-of-the-art alternatives.

Simultaneous Prediction Intervals for Patient-Specific Survival Curves

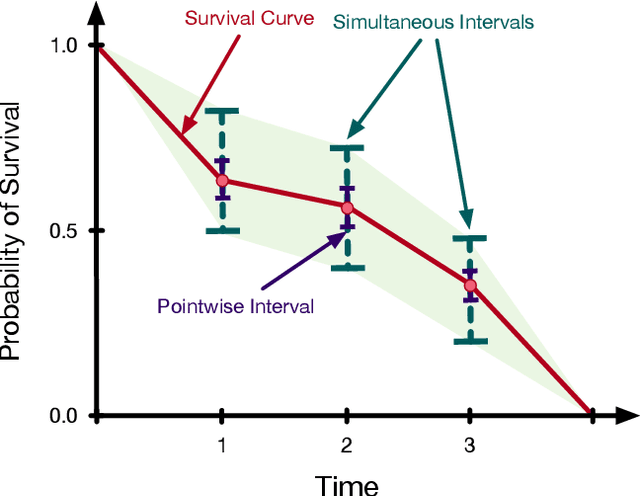
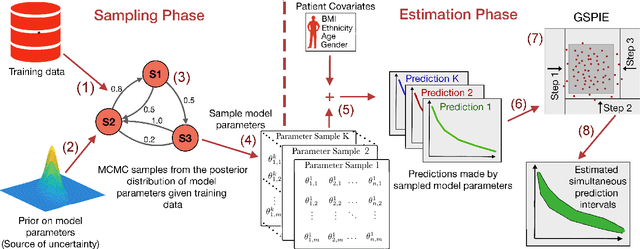
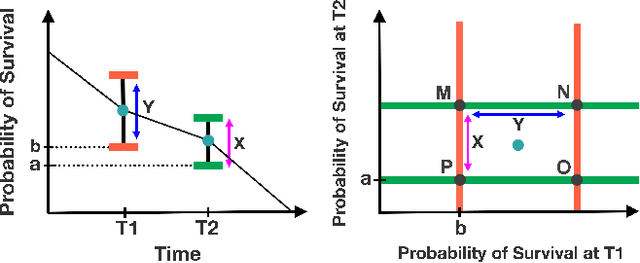
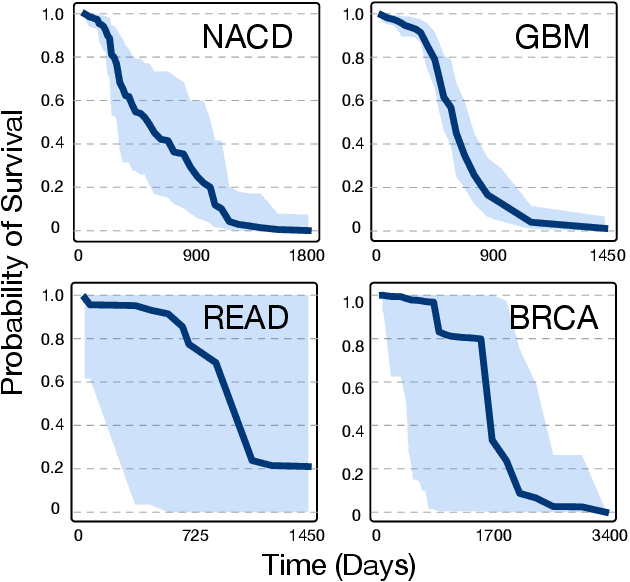
Accurate models of patient survival probabilities provide important information to clinicians prescribing care for life-threatening and terminal ailments. A recently developed class of models - known as individual survival distributions (ISDs) - produces patient-specific survival functions that offer greater descriptive power of patient outcomes than was previously possible. Unfortunately, at the time of writing, ISD models almost universally lack uncertainty quantification. In this paper, we demonstrate that an existing method for estimating simultaneous prediction intervals from samples can easily be adapted for patient-specific survival curve analysis and yields accurate results. Furthermore, we introduce both a modification to the existing method and a novel method for estimating simultaneous prediction intervals and show that they offer competitive performance. It is worth emphasizing that these methods are not limited to survival analysis and can be applied in any context in which sampling the distribution of interest is tractable. Code is available at https://github.com/ssokota/spie .

The Challenge of Predicting Meal-to-meal Blood Glucose Concentrations for Patients with Type I Diabetes

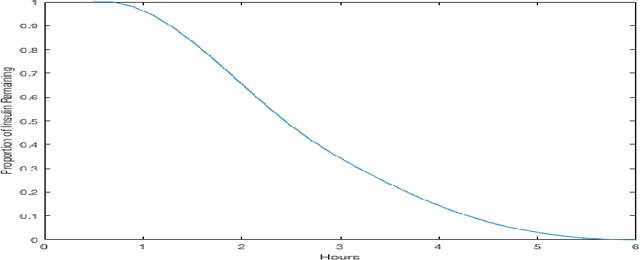
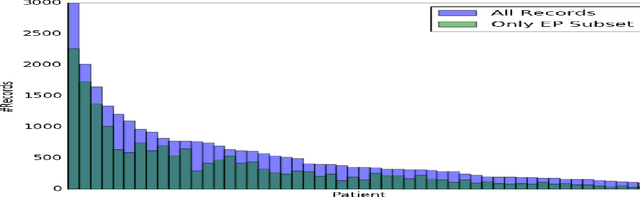
Patients with Type I Diabetes (T1D) must take insulin injections to prevent the serious long term effects of hyperglycemia - high blood glucose (BG). Patients must also be careful not to inject too much insulin because this could induce hypoglycemia (low BG), which can potentially be fatal. Patients therefore follow a "regimen" that determines how much insulin to inject at certain times. Current methods for managing this disease require adjusting the patient's regimen over time based on the disease's behavior (recorded in the patient's diabetes diary). If we can accurately predict a patient's future BG values from his/her current features (e.g., predicting today's lunch BG value given today's diabetes diary entry for breakfast, including insulin injections, and perhaps earlier entries), then it is relatively easy to produce an effective regimen. This study explores the challenges of BG modeling by applying several machine learning algorithms and various data preprocessing variations (corresponding to 312 [learner, preprocessed-dataset] combinations), to a new T1D dataset containing 29 601 entries from 47 different patients. Our most accurate predictor is a weighted ensemble of two Gaussian Process Regression models, which achieved an errL1 loss of 2.70 mmol/L (48.65 mg/dl). This was an unexpectedly poor result given that one can obtain an errL1 of 2.91 mmol/L (52.43 mg/dl) using the naive approach of simply predicting the patient's average BG. For each of data-variant/model combination we report several evaluation metrics, including glucose-specific metrics, and find similarly disappointing results (the best model was only incrementally better than the simplest measure). These results suggest that the diabetes diary data that is typically collected may not be sufficient to produce accurate BG prediction models; additional data may be necessary to build accurate BG prediction models.

Gene Expression based Survival Prediction for Cancer Patients: A Topic Modeling Approach

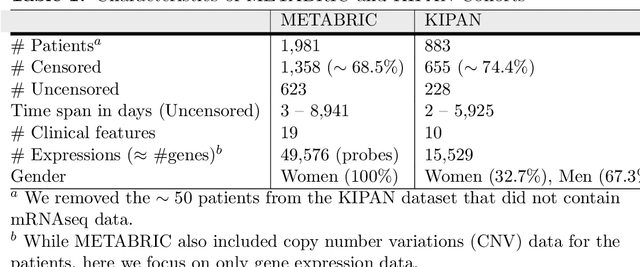
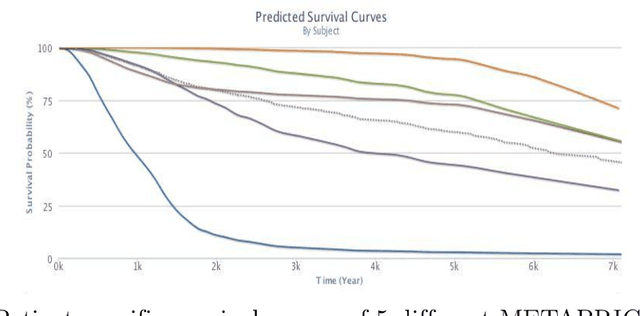
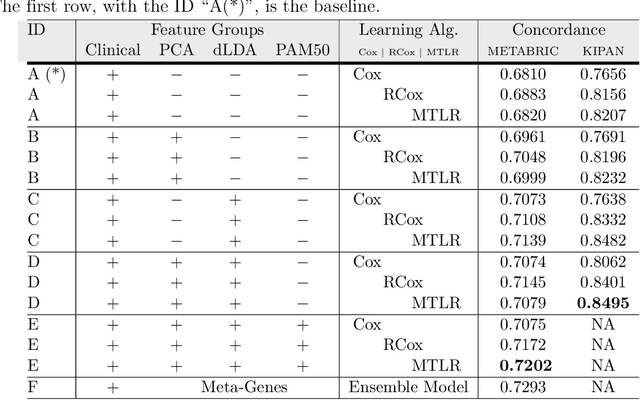
Cancer is one of the leading cause of death, worldwide. Many believe that genomic data will enable us to better predict the survival time of these patients, which will lead to better, more personalized treatment options and patient care. As standard survival prediction models have a hard time coping with the high-dimensionality of such gene expression (GE) data, many projects use some dimensionality reduction techniques to overcome this hurdle. We introduce a novel methodology, inspired by topic modeling from the natural language domain, to derive expressive features from the high-dimensional GE data. There, a document is represented as a mixture over a relatively small number of topics, where each topic corresponds to a distribution over the words; here, to accommodate the heterogeneity of a patient's cancer, we represent each patient (~document) as a mixture over cancer-topics, where each cancer-topic is a mixture over GE values (~words). This required some extensions to the standard LDA model eg: to accommodate the "real-valued" expression values - leading to our novel "discretized" Latent Dirichlet Allocation (dLDA) procedure. We initially focus on the METABRIC dataset, which describes breast cancer patients using the r=49,576 GE values, from microarrays. Our results show that our approach provides survival estimates that are more accurate than standard models, in terms of the standard Concordance measure. We then validate this approach by running it on the Pan-kidney (KIPAN) dataset, over r=15,529 GE values - here using the mRNAseq modality - and find that it again achieves excellent results. In both cases, we also show that the resulting model is calibrated, using the recent "D-calibrated" measure. These successes, in two different cancer types and expression modalities, demonstrates the generality, and the effectiveness, of this approach.

Effective Ways to Build and Evaluate Individual Survival Distributions

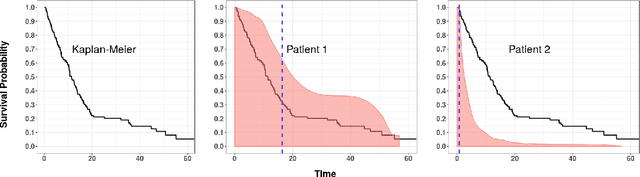
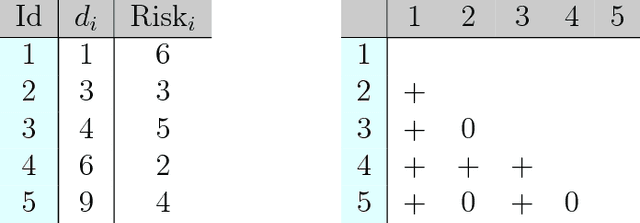
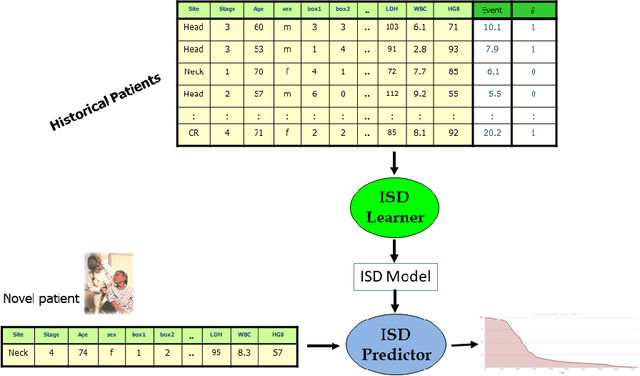
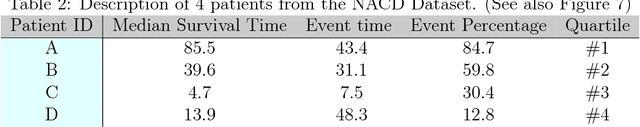
An accurate model of a patient's individual survival distribution can help determine the appropriate treatment for terminal patients. Unfortunately, risk scores (e.g., from Cox Proportional Hazard models) do not provide survival probabilities, single-time probability models (e.g., the Gail model, predicting 5 year probability) only provide for a single time point, and standard Kaplan-Meier survival curves provide only population averages for a large class of patients meaning they are not specific to individual patients. This motivates an alternative class of tools that can learn a model which provides an individual survival distribution which gives survival probabilities across all times - such as extensions to the Cox model, Accelerated Failure Time, an extension to Random Survival Forests, and Multi-Task Logistic Regression. This paper first motivates such "individual survival distribution" (ISD) models, and explains how they differ from standard models. It then discusses ways to evaluate such models - namely Concordance, 1-Calibration, Brier score, and various versions of L1-loss - and then motivates and defines a novel approach "D-Calibration", which determines whether a model's probability estimates are meaningful. We also discuss how these measures differ, and use them to evaluate several ISD prediction tools, over a range of survival datasets.

Learning Neural Markers of Schizophrenia Disorder Using Recurrent Neural Networks

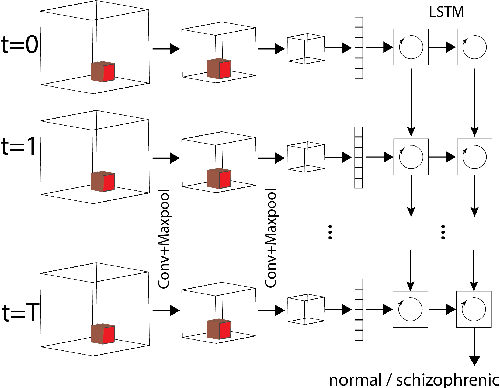
Smart systems that can accurately diagnose patients with mental disorders and identify effective treatments based on brain functional imaging data are of great applicability and are gaining much attention. Most previous machine learning studies use hand-designed features, such as functional connectivity, which does not maintain the potential useful information in the spatial relationship between brain regions and the temporal profile of the signal in each region. Here we propose a new method based on recurrent-convolutional neural networks to automatically learn useful representations from segments of 4-D fMRI recordings. Our goal is to exploit both spatial and temporal information in the functional MRI movie (at the whole-brain voxel level) for identifying patients with schizophrenia.

Stochastic Neural Networks with Monotonic Activation Functions

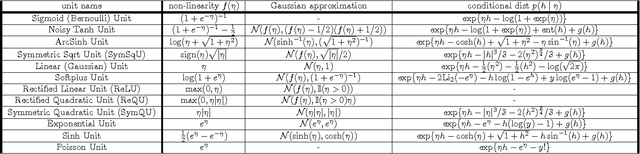
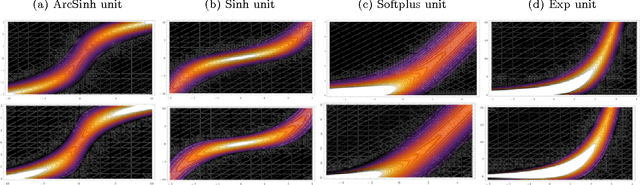
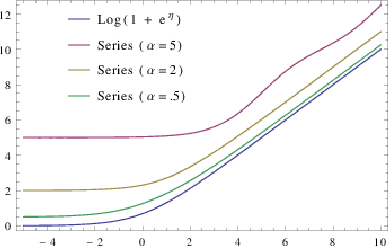
We propose a Laplace approximation that creates a stochastic unit from any smooth monotonic activation function, using only Gaussian noise. This paper investigates the application of this stochastic approximation in training a family of Restricted Boltzmann Machines (RBM) that are closely linked to Bregman divergences. This family, that we call exponential family RBM (Exp-RBM), is a subset of the exponential family Harmoniums that expresses family members through a choice of smooth monotonic non-linearity for each neuron. Using contrastive divergence along with our Gaussian approximation, we show that Exp-RBM can learn useful representations using novel stochastic units.

Boolean Matrix Factorization and Noisy Completion via Message Passing

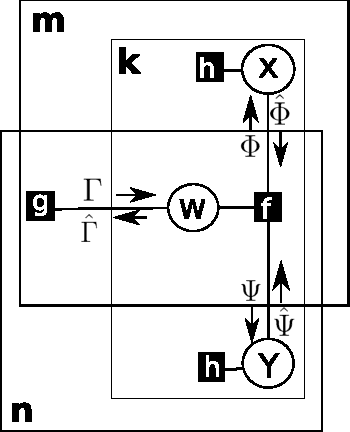
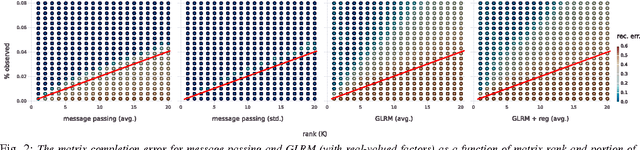
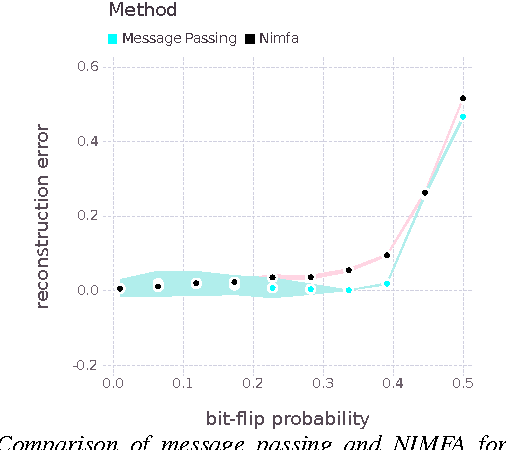
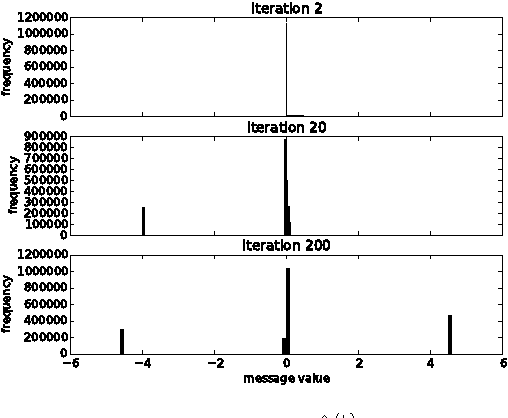
Boolean matrix factorization and Boolean matrix completion from noisy observations are desirable unsupervised data-analysis methods due to their interpretability, but hard to perform due to their NP-hardness. We treat these problems as maximum a posteriori inference problems in a graphical model and present a message passing approach that scales linearly with the number of observations and factors. Our empirical study demonstrates that message passing is able to recover low-rank Boolean matrices, in the boundaries of theoretically possible recovery and compares favorably with state-of-the-art in real-world applications, such collaborative filtering with large-scale Boolean data.

Revisiting Algebra and Complexity of Inference in Graphical Models

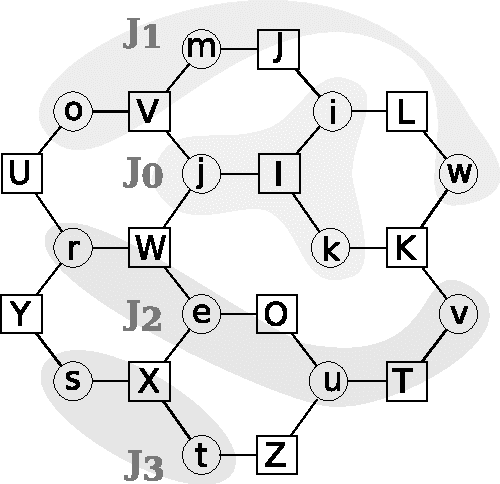
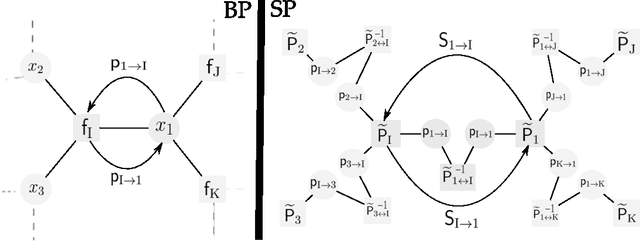
This paper studies the form and complexity of inference in graphical models using the abstraction offered by algebraic structures. In particular, we broadly formalize inference problems in graphical models by viewing them as a sequence of operations based on commutative semigroups. We then study the computational complexity of inference by organizing various problems into an "inference hierarchy". When the underlying structure of an inference problem is a commutative semiring -- i.e. a combination of two commutative semigroups with the distributive law -- a message passing procedure called belief propagation can leverage this distributive law to perform polynomial-time inference for certain problems. After establishing the NP-hardness of inference in any commutative semiring, we investigate the relation between algebraic properties in this setting and further show that polynomial-time inference using distributive law does not (trivially) extend to inference problems that are expressed using more than two commutative semigroups. We then extend the algebraic treatment of message passing procedures to survey propagation, providing a novel perspective using a combination of two commutative semirings. This formulation generalizes the application of survey propagation to new settings.