Richard G. Baraniuk
Drawing early-bird tickets: Towards more efficient training of deep networks
Sep 26, 2019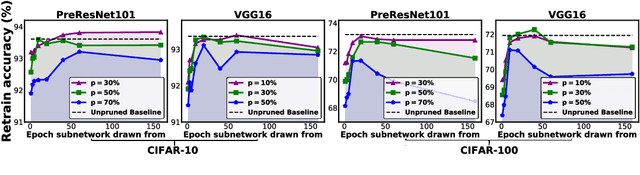
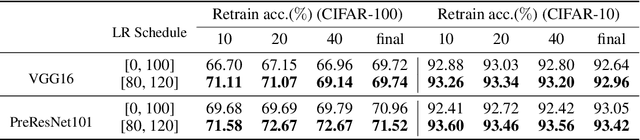
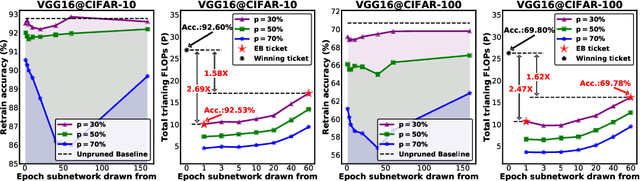
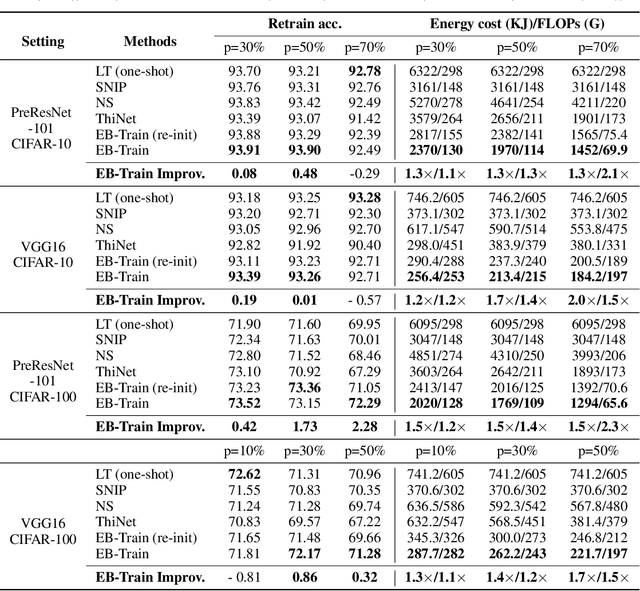
Abstract:(Frankle & Carbin, 2019) shows that there exist winning tickets (small but critical subnetworks) for dense, randomly initialized networks, that can be trained alone to achieve comparable accuracies to the latter in a similar number of iterations. However, the identification of these winning tickets still requires the costly train-prune-retrain process, limiting their practical benefits. In this paper, we discover for the first time that the winning tickets can be identified at the very early training stage, which we term as early-bird (EB) tickets, via low-cost training schemes (e.g., early stopping and low-precision training) at large learning rates. Our finding of EB tickets is consistent with recently reported observations that the key connectivity patterns of neural networks emerge early. Furthermore, we propose a mask distance metric that can be used to identify EB tickets with low computational overhead, without needing to know the true winning tickets that emerge after the full training. Finally, we leverage the existence of EB tickets and the proposed mask distance to develop efficient training methods, which are achieved by first identifying EB tickets via low-cost schemes, and then continuing to train merely the EB tickets towards the target accuracy. Experiments based on various deep networks and datasets validate: 1) the existence of EB tickets, and the effectiveness of mask distance in efficiently identifying them; and 2) that the proposed efficient training via EB tickets can achieve up to 4.7x energy savings while maintaining comparable or even better accuracy, demonstrating a promising and easily adopted method for tackling cost-prohibitive deep network training.
Out-of-Distribution Detection Using Neural Rendering Generative Models
Jul 10, 2019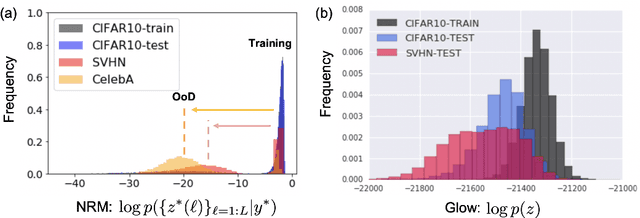

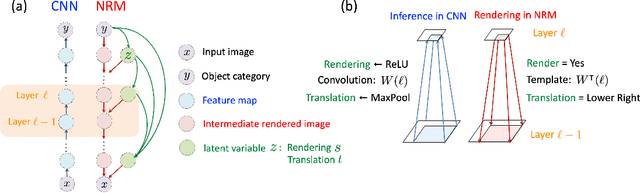
Abstract:Out-of-distribution (OoD) detection is a natural downstream task for deep generative models, due to their ability to learn the input probability distribution. There are mainly two classes of approaches for OoD detection using deep generative models, viz., based on likelihood measure and the reconstruction loss. However, both approaches are unable to carry out OoD detection effectively, especially when the OoD samples have smaller variance than the training samples. For instance, both flow based and VAE models assign higher likelihood to images from SVHN when trained on CIFAR-10 images. We use a recently proposed generative model known as neural rendering model (NRM) and derive metrics for OoD. We show that NRM unifies both approaches since it provides a likelihood estimate and also carries out reconstruction in each layer of the neural network. Among various measures, we found the joint likelihood of latent variables to be the most effective one for OoD detection. Our results show that when trained on CIFAR-10, lower likelihood (of latent variables) is assigned to SVHN images. Additionally, we show that this metric is consistent across other OoD datasets. To the best of our knowledge, this is the first work to show consistently lower likelihood for OoD data with smaller variance with deep generative models.
IdeoTrace: A Framework for Ideology Tracing with a Case Study on the 2016 U.S. Presidential Election
May 30, 2019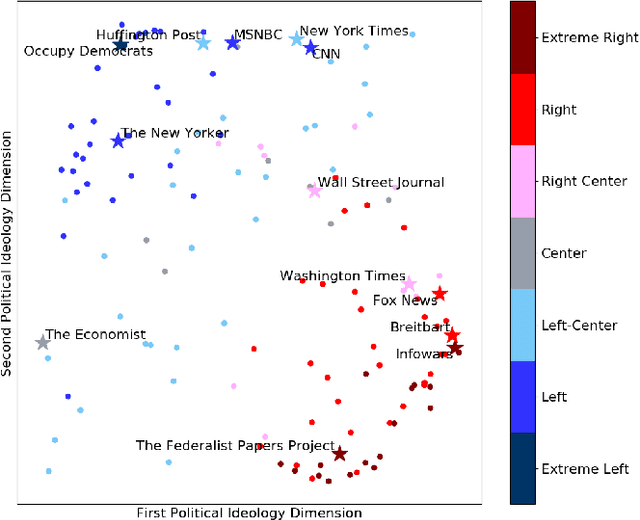
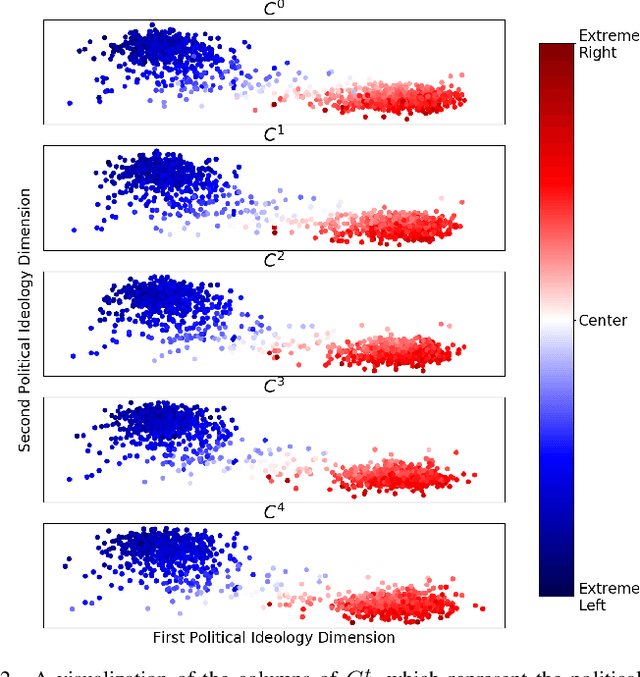
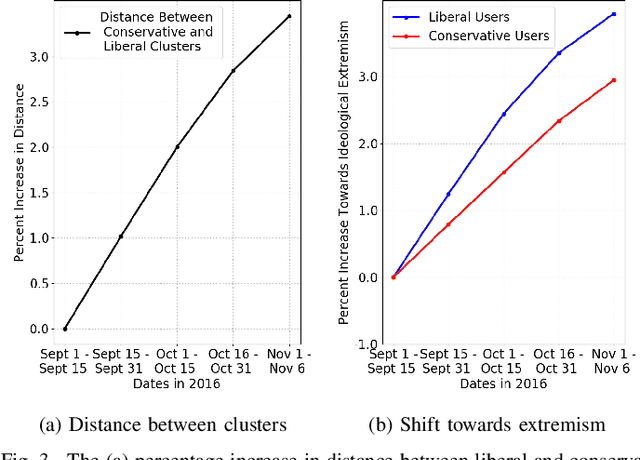
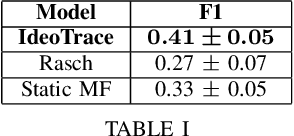
Abstract:The 2016 United States presidential election has been characterized as a period of extreme divisiveness that was exacerbated on social media by the influence of fake news, trolls, and social bots. However, the extent to which the public became more polarized in response to these influences over the course of the election is not well understood. In this paper we propose IdeoTrace, a framework for (i) jointly estimating the ideology of social media users and news websites and (ii) tracing changes in user ideology over time. We apply this framework to the last two months of the election period for a group of 47508 Twitter users and demonstrate that both liberal and conservative users became more polarized over time.
Thresholding Graph Bandits with GrAPL
May 22, 2019
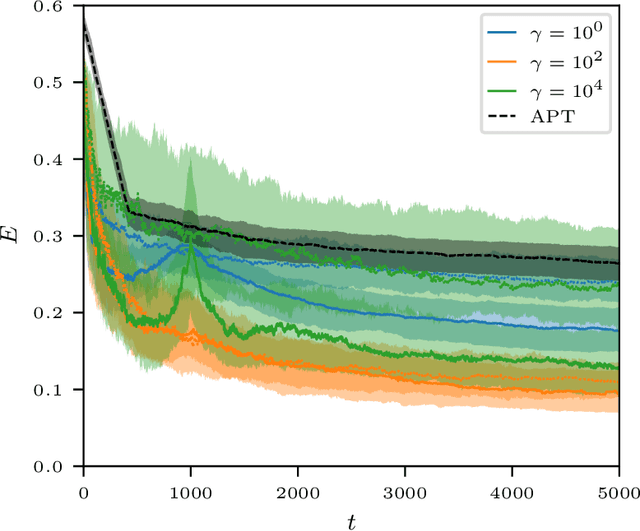
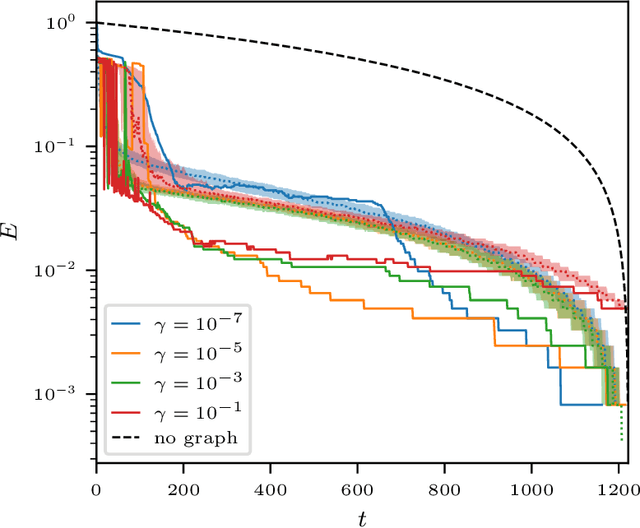
Abstract:In this paper, we introduce a new online decision making paradigm that we call Thresholding Graph Bandits. The main goal is to efficiently identify a subset of arms in a multi-armed bandit problem whose means are above a specified threshold. While traditionally in such problems, the arms are assumed to be independent, in our paradigm we further suppose that we have access to the similarity between the arms in the form of a graph, allowing us gain information about the arm means in fewer samples. Such settings play a key role in a wide range of modern decision making problems where rapid decisions need to be made in spite of the large number of options available at each time. We present GrAPL, a novel algorithm for the thresholding graph bandit problem. We demonstrate theoretically that this algorithm is effective in taking advantage of the graph structure when available and the reward function homophily (that strongly connected arms have similar rewards) when favorable. We confirm these theoretical findings via experiments on both synthetic and real data.
RACE: Sub-Linear Memory Sketches for Approximate Near-Neighbor Search on Streaming Data
Apr 09, 2019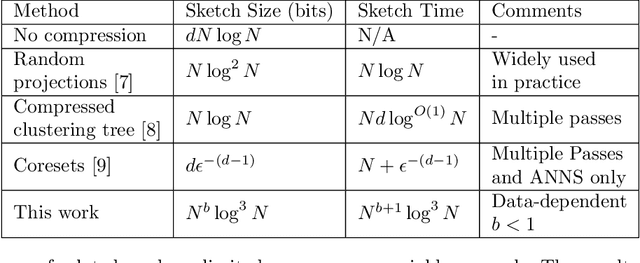
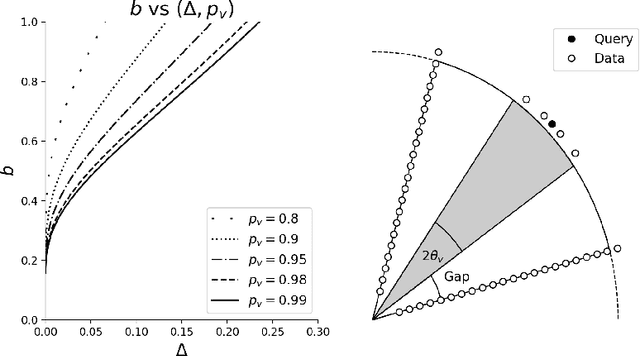
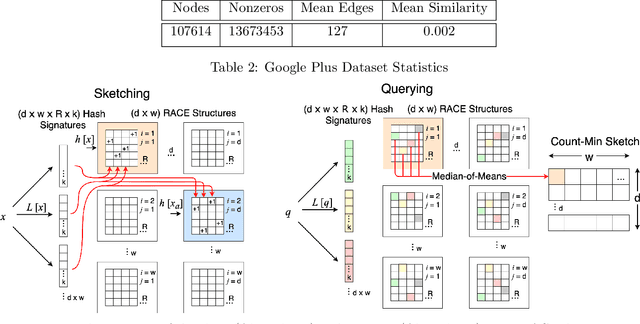
Abstract:We present the first sublinear memory sketch which can be queried to find the $v$ nearest neighbors in a dataset. Our online sketching algorithm can compress an $N$-element dataset to a sketch of size $O(N^b \log^3{N})$ in $O(N^{b+1} \log^3{N})$ time, where $b < 1$ when the query satisfies a data-dependent near-neighbor stability condition. We achieve data-dependent sublinear space by combining recent advances in locality sensitive hashing (LSH)-based estimators with compressed sensing. Our results shed new light on the memory-accuracy tradeoff for near-neighbor search. The techniques presented reveal a deep connection between the fundamental compressed sensing (or heavy hitters) recovery problem and near-neighbor search, leading to new insight for geometric search problems and implications for sketching algorithms.
Representing Formal Languages: A Comparison Between Finite Automata and Recurrent Neural Networks
Feb 27, 2019
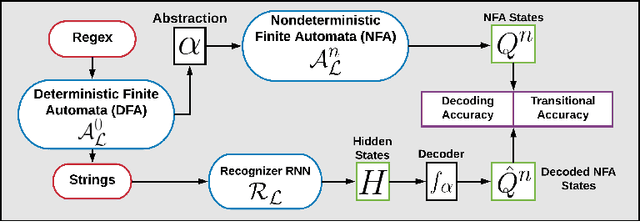

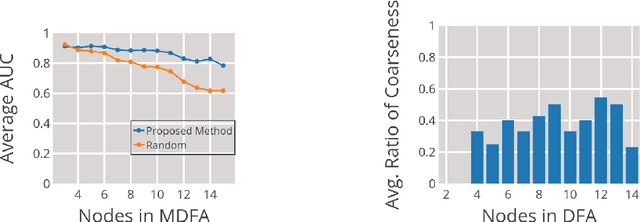
Abstract:We investigate the internal representations that a recurrent neural network (RNN) uses while learning to recognize a regular formal language. Specifically, we train a RNN on positive and negative examples from a regular language, and ask if there is a simple decoding function that maps states of this RNN to states of the minimal deterministic finite automaton (MDFA) for the language. Our experiments show that such a decoding function indeed exists, and that it maps states of the RNN not to MDFA states, but to states of an {\em abstraction} obtained by clustering small sets of MDFA states into "superstates". A qualitative analysis reveals that the abstraction often has a simple interpretation. Overall, the results suggest a strong structural relationship between internal representations used by RNNs and finite automata, and explain the well-known ability of RNNs to recognize formal grammatical structure.
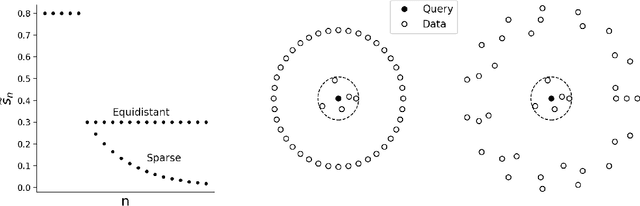
Adaptive Estimation for Approximate k-Nearest-Neighbor Computations
Feb 25, 2019
Abstract:Algorithms often carry out equally many computations for "easy" and "hard" problem instances. In particular, algorithms for finding nearest neighbors typically have the same running time regardless of the particular problem instance. In this paper, we consider the approximate k-nearest-neighbor problem, which is the problem of finding a subset of O(k) points in a given set of points that contains the set of k nearest neighbors of a given query point. We propose an algorithm based on adaptively estimating the distances, and show that it is essentially optimal out of algorithms that are only allowed to adaptively estimate distances. We then demonstrate both theoretically and experimentally that the algorithm can achieve significant speedups relative to the naive method.
From Hard to Soft: Understanding Deep Network Nonlinearities via Vector Quantization and Statistical Inference
Oct 22, 2018
Abstract:Nonlinearity is crucial to the performance of a deep (neural) network (DN). To date there has been little progress understanding the menagerie of available nonlinearities, but recently progress has been made on understanding the r\^ole played by piecewise affine and convex nonlinearities like the ReLU and absolute value activation functions and max-pooling. In particular, DN layers constructed from these operations can be interpreted as {\em max-affine spline operators} (MASOs) that have an elegant link to vector quantization (VQ) and $K$-means. While this is good theoretical progress, the entire MASO approach is predicated on the requirement that the nonlinearities be piecewise affine and convex, which precludes important activation functions like the sigmoid, hyperbolic tangent, and softmax. {\em This paper extends the MASO framework to these and an infinitely large class of new nonlinearities by linking deterministic MASOs with probabilistic Gaussian Mixture Models (GMMs).} We show that, under a GMM, piecewise affine, convex nonlinearities like ReLU, absolute value, and max-pooling can be interpreted as solutions to certain natural "hard" VQ inference problems, while sigmoid, hyperbolic tangent, and softmax can be interpreted as solutions to corresponding "soft" VQ inference problems. We further extend the framework by hybridizing the hard and soft VQ optimizations to create a $\beta$-VQ inference that interpolates between hard, soft, and linear VQ inference. A prime example of a $\beta$-VQ DN nonlinearity is the {\em swish} nonlinearity, which offers state-of-the-art performance in a range of computer vision tasks but was developed ad hoc by experimentation. Finally, we validate with experiments an important assertion of our theory, namely that DN performance can be significantly improved by enforcing orthogonality in its linear filters.
prDeep: Robust Phase Retrieval with a Flexible Deep Network
Jun 29, 2018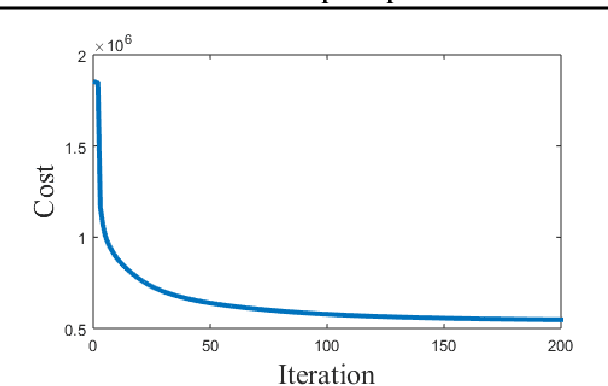
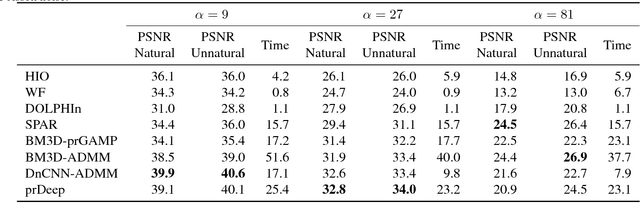
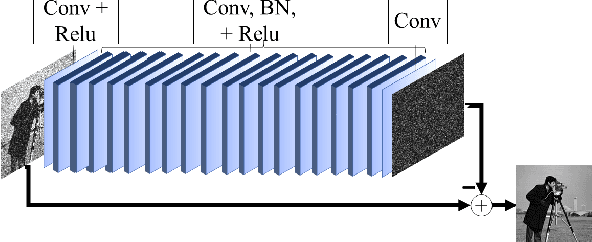
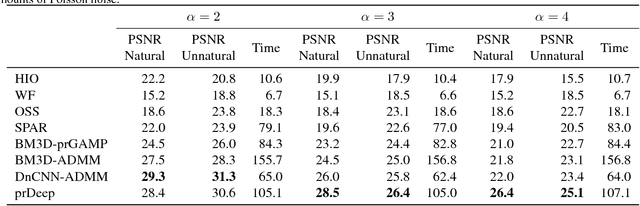
Abstract:Phase retrieval algorithms have become an important component in many modern computational imaging systems. For instance, in the context of ptychography and speckle correlation imaging, they enable imaging past the diffraction limit and through scattering media, respectively. Unfortunately, traditional phase retrieval algorithms struggle in the presence of noise. Progress has been made recently on more robust algorithms using signal priors, but at the expense of limiting the range of supported measurement models (e.g., to Gaussian or coded diffraction patterns). In this work we leverage the regularization-by-denoising framework and a convolutional neural network denoiser to create prDeep, a new phase retrieval algorithm that is both robust and broadly applicable. We test and validate prDeep in simulation to demonstrate that it is robust to noise and can handle a variety of system models. A MatConvNet implementation of prDeep is available at https://github.com/ricedsp/prDeep.
MISSION: Ultra Large-Scale Feature Selection using Count-Sketches
Jun 12, 2018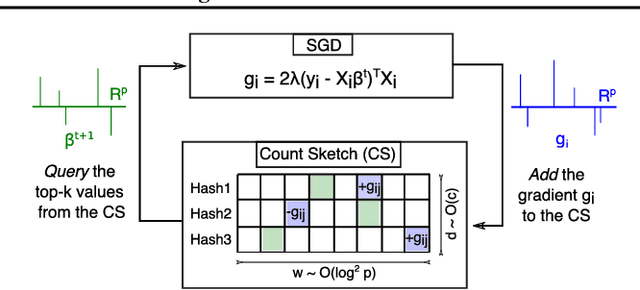


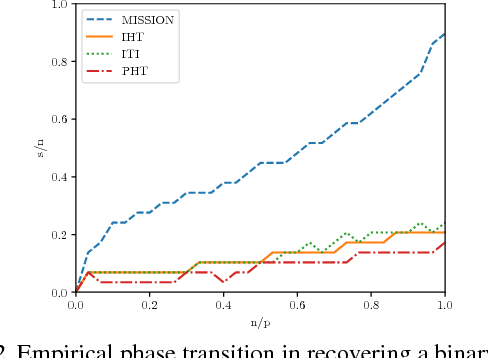
Abstract:Feature selection is an important challenge in machine learning. It plays a crucial role in the explainability of machine-driven decisions that are rapidly permeating throughout modern society. Unfortunately, the explosion in the size and dimensionality of real-world datasets poses a severe challenge to standard feature selection algorithms. Today, it is not uncommon for datasets to have billions of dimensions. At such scale, even storing the feature vector is impossible, causing most existing feature selection methods to fail. Workarounds like feature hashing, a standard approach to large-scale machine learning, helps with the computational feasibility, but at the cost of losing the interpretability of features. In this paper, we present MISSION, a novel framework for ultra large-scale feature selection that performs stochastic gradient descent while maintaining an efficient representation of the features in memory using a Count-Sketch data structure. MISSION retains the simplicity of feature hashing without sacrificing the interpretability of the features while using only O(log^2(p)) working memory. We demonstrate that MISSION accurately and efficiently performs feature selection on real-world, large-scale datasets with billions of dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge