"What is the value of {templates}?" Rethinking Document Information Extraction Datasets for LLMs

The rise of large language models (LLMs) for visually rich document understanding (VRDU) has kindled a need for prompt-response, document-based datasets. As annotating new datasets from scratch is labor-intensive, the existing literature has generated prompt-response datasets from available resources using simple templates. For the case of key information extraction (KIE), one of the most common VRDU tasks, past work has typically employed the template "What is the value for the {key}?". However, given the variety of questions encountered in the wild, simple and uniform templates are insufficient for creating robust models in research and industrial contexts. In this work, we present K2Q, a diverse collection of five datasets converted from KIE to a prompt-response format using a plethora of bespoke templates. The questions in K2Q can span multiple entities and be extractive or boolean. We empirically compare the performance of seven baseline generative models on K2Q with zero-shot prompting. We further compare three of these models when training on K2Q versus training on simpler templates to motivate the need of our work. We find that creating diverse and intricate KIE questions enhances the performance and robustness of VRDU models. We hope this work encourages future studies on data quality for generative model training.

Fine-Tuning Language Models with Differential Privacy through Adaptive Noise Allocation

Language models are capable of memorizing detailed patterns and information, leading to a double-edged effect: they achieve impressive modeling performance on downstream tasks with the stored knowledge but also raise significant privacy concerns. Traditional differential privacy based training approaches offer robust safeguards by employing a uniform noise distribution across all parameters. However, this overlooks the distinct sensitivities and contributions of individual parameters in privacy protection and often results in suboptimal models. To address these limitations, we propose ANADP, a novel algorithm that adaptively allocates additive noise based on the importance of model parameters. We demonstrate that ANADP narrows the performance gap between regular fine-tuning and traditional DP fine-tuning on a series of datasets while maintaining the required privacy constraints.

BuDDIE: A Business Document Dataset for Multi-task Information Extraction

The field of visually rich document understanding (VRDU) aims to solve a multitude of well-researched NLP tasks in a multi-modal domain. Several datasets exist for research on specific tasks of VRDU such as document classification (DC), key entity extraction (KEE), entity linking, visual question answering (VQA), inter alia. These datasets cover documents like invoices and receipts with sparse annotations such that they support one or two co-related tasks (e.g., entity extraction and entity linking). Unfortunately, only focusing on a single specific of documents or task is not representative of how documents often need to be processed in the wild - where variety in style and requirements is expected. In this paper, we introduce BuDDIE (Business Document Dataset for Information Extraction), the first multi-task dataset of 1,665 real-world business documents that contains rich and dense annotations for DC, KEE, and VQA. Our dataset consists of publicly available business entity documents from US state government websites. The documents are structured and vary in their style and layout across states and types (e.g., forms, certificates, reports, etc.). We provide data variety and quality metrics for BuDDIE as well as a series of baselines for each task. Our baselines cover traditional textual, multi-modal, and large language model approaches to VRDU.

Log Summarisation for Defect Evolution Analysis

Log analysis and monitoring are essential aspects in software maintenance and identifying defects. In particular, the temporal nature and vast size of log data leads to an interesting and important research question: How can logs be summarised and monitored over time? While this has been a fundamental topic of research in the software engineering community, work has typically focused on heuristic-, syntax-, or static-based methods. In this work, we suggest an online semantic-based clustering approach to error logs that dynamically updates the log clusters to enable monitoring code error life-cycles. We also introduce a novel metric to evaluate the performance of temporal log clusters. We test our system and evaluation metric with an industrial dataset and find that our solution outperforms similar systems. We hope that our work encourages further temporal exploration in defect datasets.

Translating between SQL Dialects for Cloud Migration

Migrations of systems from on-site premises to the cloud has been a fundamental endeavor by many industrial institutions. A crucial component of such cloud migrations is the transition of databases to be hosted online. In this work, we consider the difficulties of this migration for SQL databases. While SQL is one of the prominent methods for storing database procedures, there are a plethora of different SQL dialects (e.g., MySQL, Postgres, etc.) which can complicate migrations when the on-premise SQL dialect differs to the dialect hosted on the cloud. Tools exist by common cloud provides such as AWS and Azure to aid in translating between dialects in order to mitigate the majority of the difficulties. However, these tools do not successfully translate $100\%$ of the code. Consequently, software engineers must manually convert the remainder of the untranslated database. For large organizations, this task quickly becomes intractable and so more innovative solutions are required. We consider this challenge a novel yet vital industrial research problem for any large corporation that is considering cloud migrations. Furthermore, we introduce potential avenues of research to tackle this challenge that have yielded promising preliminary results.

TreeForm: End-to-end Annotation and Evaluation for Form Document Parsing

Visually Rich Form Understanding (VRFU) poses a complex research problem due to the documents' highly structured nature and yet highly variable style and content. Current annotation schemes decompose form understanding and omit key hierarchical structure, making development and evaluation of end-to-end models difficult. In this paper, we propose a novel F1 metric to evaluate form parsers and describe a new content-agnostic, tree-based annotation scheme for VRFU: TreeForm. We provide methods to convert previous annotation schemes into TreeForm structures and evaluate TreeForm predictions using a modified version of the normalized tree-edit distance. We present initial baselines for our end-to-end performance metric and the TreeForm edit distance, averaged over the FUNSD and XFUND datasets, of 61.5 and 26.4 respectively. We hope that TreeForm encourages deeper research in annotating, modeling, and evaluating the complexities of form-like documents.

Efficient Semiring-Weighted Earley Parsing

This paper provides a reference description, in the form of a deduction system, of Earley's (1970) context-free parsing algorithm with various speed-ups. Our presentation includes a known worst-case runtime improvement from Earley's $O (N^3|G||R|)$, which is unworkable for the large grammars that arise in natural language processing, to $O (N^3|G|)$, which matches the runtime of CKY on a binarized version of the grammar $G$. Here $N$ is the length of the sentence, $|R|$ is the number of productions in $G$, and $|G|$ is the total length of those productions. We also provide a version that achieves runtime of $O (N^3|M|)$ with $|M| \leq |G|$ when the grammar is represented compactly as a single finite-state automaton $M$ (this is partly novel). We carefully treat the generalization to semiring-weighted deduction, preprocessing the grammar like Stolcke (1995) to eliminate deduction cycles, and further generalize Stolcke's method to compute the weights of sentence prefixes. We also provide implementation details for efficient execution, ensuring that on a preprocessed grammar, the semiring-weighted versions of our methods have the same asymptotic runtime and space requirements as the unweighted methods, including sub-cubic runtime on some grammars.

UniMorph 4.0: Universal Morphology

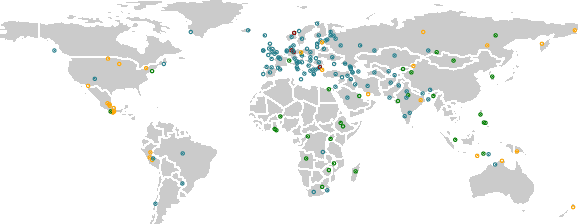
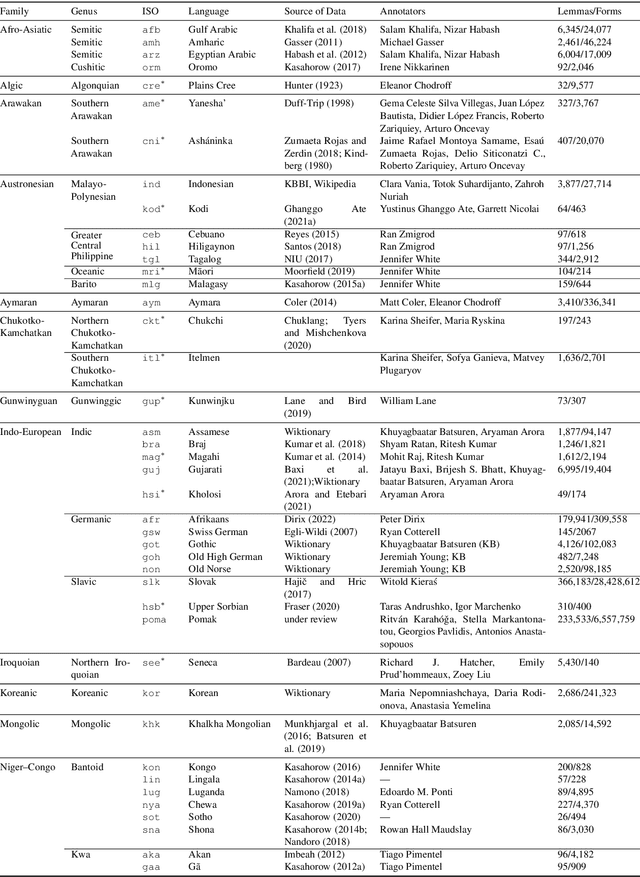
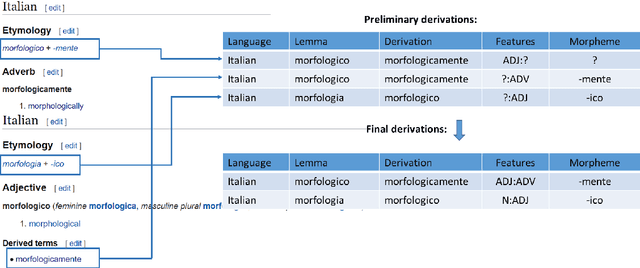
The Universal Morphology (UniMorph) project is a collaborative effort providing broad-coverage instantiated normalized morphological inflection tables for hundreds of diverse world languages. The project comprises two major thrusts: a language-independent feature schema for rich morphological annotation and a type-level resource of annotated data in diverse languages realizing that schema. This paper presents the expansions and improvements made on several fronts over the last couple of years (since McCarthy et al. (2020)). Collaborative efforts by numerous linguists have added 67 new languages, including 30 endangered languages. We have implemented several improvements to the extraction pipeline to tackle some issues, e.g. missing gender and macron information. We have also amended the schema to use a hierarchical structure that is needed for morphological phenomena like multiple-argument agreement and case stacking, while adding some missing morphological features to make the schema more inclusive. In light of the last UniMorph release, we also augmented the database with morpheme segmentation for 16 languages. Lastly, this new release makes a push towards inclusion of derivational morphology in UniMorph by enriching the data and annotation schema with instances representing derivational processes from MorphyNet.

Exact Paired-Permutation Testing for Structured Test Statistics

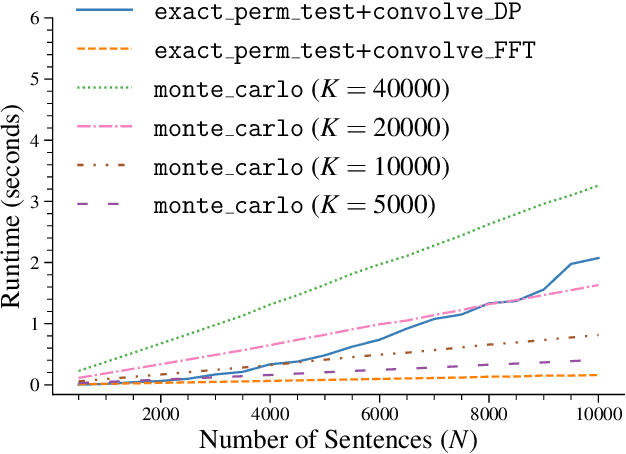
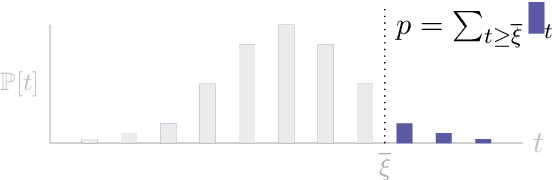
Significance testing -- especially the paired-permutation test -- has played a vital role in developing NLP systems to provide confidence that the difference in performance between two systems (i.e., the test statistic) is not due to luck. However, practitioners rely on Monte Carlo approximation to perform this test due to a lack of a suitable exact algorithm. In this paper, we provide an efficient exact algorithm for the paired-permutation test for a family of structured test statistics. Our algorithm runs in $\mathcal{O}(GN (\log GN )(\log N ))$ time where $N$ is the dataset size and $G$ is the range of the test statistic. We found that our exact algorithm was $10$x faster than the Monte Carlo approximation with $20000$ samples on a common dataset.

Efficient Sampling of Dependency Structures

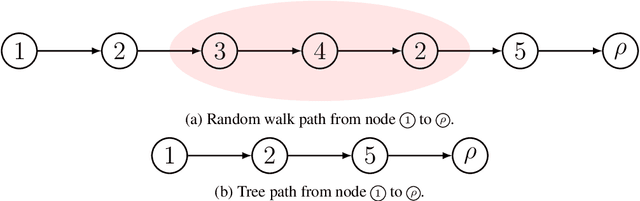
Probabilistic distributions over spanning trees in directed graphs are a fundamental model of dependency structure in natural language processing, syntactic dependency trees. In NLP, dependency trees often have an additional root constraint: only one edge may emanate from the root. However, no sampling algorithm has been presented in the literature to account for this additional constraint. In this paper, we adapt two spanning tree sampling algorithms to faithfully sample dependency trees from a graph subject to the root constraint. Wilson (1996)'s sampling algorithm has a running time of $\mathcal{O}(H)$ where $H$ is the mean hitting time of the graph. Colbourn (1996)'s sampling algorithm has a running time of $\mathcal{O}(N^3)$, which is often greater than the mean hitting time of a directed graph. Additionally, we build upon Colbourn's algorithm and present a novel extension that can sample $K$ trees without replacement in $\mathcal{O}(K N^3 + K^2 N)$ time. To the best of our knowledge, no algorithm has been given for sampling spanning trees without replacement from a directed graph.