Metasurfaces-Integrated Wireless Neural Networks for Lightweight Over-The-Air Edge Inference

The upcoming sixth Generation (6G) of wireless networks envisions ultra-low latency and energy efficient Edge Inference (EI) for diverse Internet of Things (IoT) applications. However, traditional digital hardware for machine learning is power intensive, motivating the need for alternative computation paradigms. Over-The-Air (OTA) computation is regarded as an emerging transformative approach assigning the wireless channel to actively perform computational tasks. This article introduces the concept of Metasurfaces-Integrated Neural Networks (MINNs), a physical-layer-enabled deep learning framework that leverages programmable multi-layer metasurface structures and Multiple-Input Multiple-Output (MIMO) channels to realize computational layers in the wave propagation domain. The MINN system is conceptualized as three modules: Encoder, Channel (uncontrollable propagation features and metasurfaces), and Decoder. The first and last modules, realized respectively at the multi-antenna transmitter and receiver, consist of conventional digital or purposely designed analog Deep Neural Network (DNN) layers, and the metasurfaces responses of the Channel module are optimized alongside all modules as trainable weights. This architecture enables computation offloading into the end-to-end physical layer, flexibly among its constituent modules, achieving performance comparable to fully digital DNNs while significantly reducing power consumption. The training of the MINN framework, two representative variations, and performance results for indicative applications are presented, highlighting the potential of MINNs as a lightweight and sustainable solution for future EI-enabled wireless systems. The article is concluded with a list of open challenges and promising research directions.

Federated Latent Space Alignment for Multi-user Semantic Communications

Semantic communication aims to convey meaning for effective task execution, but differing latent representations in AI-native devices can cause semantic mismatches that hinder mutual understanding. This paper introduces a novel approach to mitigating latent space misalignment in multi-agent AI- native semantic communications. In a downlink scenario, we consider an access point (AP) communicating with multiple users to accomplish a specific AI-driven task. Our method implements a protocol that shares a semantic pre-equalizer at the AP and local semantic equalizers at user devices, fostering mutual understanding and task-oriented communication while considering power and complexity constraints. To achieve this, we employ a federated optimization for the decentralized training of the semantic equalizers at the AP and user sides. Numerical results validate the proposed approach in goal-oriented semantic communication, revealing key trade-offs among accuracy, com- munication overhead, complexity, and the semantic proximity of AI-native communication devices.

Learning Dirac Spectral Transforms for Topological Signals

The Dirac operator provides a unified framework for processing signals defined over different order topological domains, such as node and edge signals. Its eigenmodes define a spectral representation that inherently captures cross-domain interactions, in contrast to conventional Hodge-Laplacian eigenmodes that operate within a single topological dimension. In this paper, we compare the two alternatives in terms of the distortion/sparsity trade-off and we show how an overcomplete basis built concatenating the two dictionaries can provide better performance with respect to each approach. Then, we propose a parameterized nonredundant transform whose eigenmodes incorporate a mode-specific mass parameter that captures the interplay between node and edge modes. Interestingly, we show that learning the mass parameters from data makes the proposed transform able to achieve the best distortion-sparsity tradeoff with respect to both complete and overcomplete bases.

Learning Consistent Causal Abstraction Networks

Causal artificial intelligence aims to enhance explainability, trustworthiness, and robustness in AI by leveraging structural causal models (SCMs). In this pursuit, recent advances formalize network sheaves and cosheaves of causal knowledge. Pushing in the same direction, we tackle the learning of consistent causal abstraction network (CAN), a sheaf-theoretic framework where (i) SCMs are Gaussian, (ii) restriction maps are transposes of constructive linear causal abstractions (CAs) adhering to the semantic embedding principle, and (iii) edge stalks correspond--up to permutation--to the node stalks of more detailed SCMs. Our problem formulation separates into edge-specific local Riemannian problems and avoids nonconvex objectives. We propose an efficient search procedure, solving the local problems with SPECTRAL, our iterative method with closed-form updates and suitable for positive definite and semidefinite covariance matrices. Experiments on synthetic data show competitive performance in the CA learning task, and successful recovery of diverse CAN structures.

Over-the-Air Goal-Oriented Communications

Goal-oriented communications offer an attractive alternative to the Shannon-based communication paradigm, where the data is never reconstructed at the Receiver (RX) side. Rather, focusing on the case of edge inference, the Transmitter (TX) and the RX cooperate to exchange features of the input data that will be used to predict an unseen attribute of them, leveraging information from collected data sets. This chapter demonstrates that the wireless channel can be used to perform computations over the data, when equipped with programmable metasurfaces. The end-to-end system of the TX, RX, and MS-based channel is treated as a single deep neural network which is trained through backpropagation to perform inference on unseen data. Using Stacked Intelligent Metasurfaces (SIM), it is shown that this Metasurfaces-Integrated Neural Network (MINN) can achieve performance comparable to fully digital neural networks under various system parameters and data sets. By offloading computations onto the channel itself, important benefits may be achieved in terms of energy consumption, arising from reduced computations at the transceivers and smaller transmission power required for successful inference.

Semantic Channel Equalization Strategies for Deep Joint Source-Channel Coding

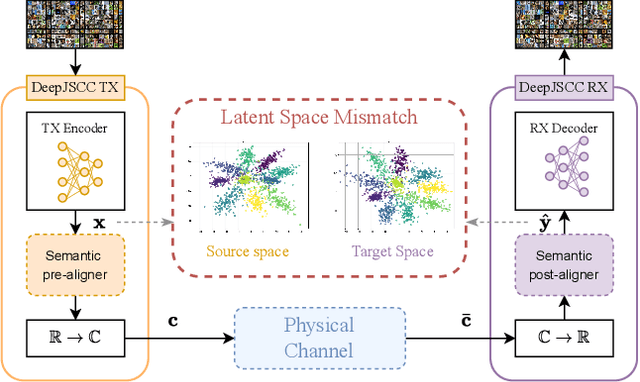
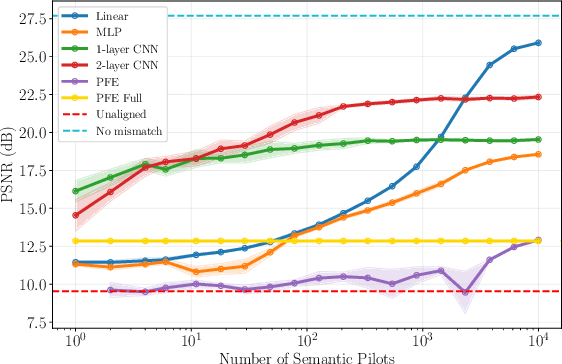
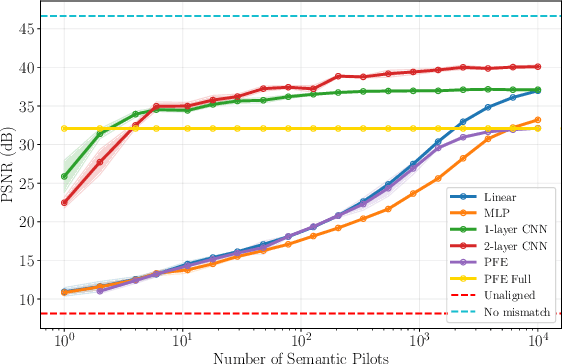
Deep joint source-channel coding (DeepJSCC) has emerged as a powerful paradigm for end-to-end semantic communications, jointly learning to compress and protect task-relevant features over noisy channels. However, existing DeepJSCC schemes assume a shared latent space at transmitter (TX) and receiver (RX) - an assumption that fails in multi-vendor deployments where encoders and decoders cannot be co-trained. This mismatch introduces "semantic noise", degrading reconstruction quality and downstream task performance. In this paper, we systematize and evaluate methods for semantic channel equalization for DeepJSCC, introducing an additional processing stage that aligns heterogeneous latent spaces under both physical and semantic impairments. We investigate three classes of aligners: (i) linear maps, which admit closed-form solutions; (ii) lightweight neural networks, offering greater expressiveness; and (iii) a Parseval-frame equalizer, which operates in zero-shot mode without the need for training. Through extensive experiments on image reconstruction over AWGN and fading channels, we quantify trade-offs among complexity, data efficiency, and fidelity, providing guidelines for deploying DeepJSCC in heterogeneous AI-native wireless networks.

Communication Efficient Split Learning of ViTs with Attention-based Double Compression

This paper proposes a novel communication-efficient Split Learning (SL) framework, named Attention-based Double Compression (ADC), which reduces the communication overhead required for transmitting intermediate Vision Transformers activations during the SL training process. ADC incorporates two parallel compression strategies. The first one merges samples' activations that are similar, based on the average attention score calculated in the last client layer; this strategy is class-agnostic, meaning that it can also merge samples having different classes, without losing generalization ability nor decreasing final results. The second strategy follows the first and discards the least meaningful tokens, further reducing the communication cost. Combining these strategies not only allows for sending less during the forward pass, but also the gradients are naturally compressed, allowing the whole model to be trained without additional tuning or approximations of the gradients. Simulation results demonstrate that Attention-based Double Compression outperforms state-of-the-art SL frameworks by significantly reducing communication overheads while maintaining high accuracy.

Latent Space Alignment for AI-Native MIMO Semantic Communications

Semantic communications focus on prioritizing the understanding of the meaning behind transmitted data and ensuring the successful completion of tasks that motivate the exchange of information. However, when devices rely on different languages, logic, or internal representations, semantic mismatches may occur, potentially hindering mutual understanding. This paper introduces a novel approach to addressing latent space misalignment in semantic communications, exploiting multiple-input multiple-output (MIMO) communications. Specifically, our method learns a MIMO precoder/decoder pair that jointly performs latent space compression and semantic channel equalization, mitigating both semantic mismatches and physical channel impairments. We explore two solutions: (i) a linear model, optimized by solving a biconvex optimization problem via the alternating direction method of multipliers (ADMM); (ii) a neural network-based model, which learns semantic MIMO precoder/decoder under transmission power budget and complexity constraints. Numerical results demonstrate the effectiveness of the proposed approach in a goal-oriented semantic communication scenario, illustrating the main trade-offs between accuracy, communication burden, and complexity of the solutions.

RIS-aided Latent Space Alignment for Semantic Channel Equalization

Semantic communication systems introduce a new paradigm in wireless communications, focusing on transmitting the intended meaning rather than ensuring strict bit-level accuracy. These systems often rely on Deep Neural Networks (DNNs) to learn and encode meaning directly from data, enabling more efficient communication. However, in multi-user settings where interacting agents are trained independently-without shared context or joint optimization-divergent latent representations across AI-native devices can lead to semantic mismatches, impeding mutual understanding even in the absence of traditional transmission errors. In this work, we address semantic mismatch in Multiple-Input Multiple-Output (MIMO) channels by proposing a joint physical and semantic channel equalization framework that leverages the presence of Reconfigurable Intelligent Surfaces (RIS). The semantic equalization is implemented as a sequence of transformations: (i) a pre-equalization stage at the transmitter; (ii) propagation through the RIS-aided channel; and (iii) a post-equalization stage at the receiver. We formulate the problem as a constrained Minimum Mean Squared Error (MMSE) optimization and propose two solutions: (i) a linear semantic equalization chain, and (ii) a non-linear DNN-based semantic equalizer. Both methods are designed to operate under semantic compression in the latent space and adhere to transmit power constraints. Through extensive evaluations, we show that the proposed joint equalization strategies consistently outperform conventional, disjoint approaches to physical and semantic channel equalization across a broad range of scenarios and wireless channel conditions.

Topological Adaptive Least Mean Squares Algorithms over Simplicial Complexes

This paper introduces a novel adaptive framework for processing dynamic flow signals over simplicial complexes, extending classical least-mean-squares (LMS) methods to high-order topological domains. Building on discrete Hodge theory, we present a topological LMS algorithm that efficiently processes streaming signals observed over time-varying edge subsets. We provide a detailed stochastic analysis of the algorithm, deriving its stability conditions, steady-state mean-square-error, and convergence speed, while exploring the impact of edge sampling on performance. We also propose strategies to design optimal edge sampling probabilities, minimizing rate while ensuring desired estimation accuracy. Assuming partial knowledge of the complex structure (e.g., the underlying graph), we introduce an adaptive topology inference method that integrates with the proposed LMS framework. Additionally, we propose a distributed version of the algorithm and analyze its stability and mean-square-error properties. Empirical results on synthetic and real-world traffic data demonstrate that our approach, in both centralized and distributed settings, outperforms graph-based LMS methods by leveraging higher-order topological features.