Model-Free Kernel Conformal Depth Measures Algorithm for Uncertainty Quantification in Regression Models in Separable Hilbert Spaces

Depth measures are powerful tools for defining level sets in emerging, non--standard, and complex random objects such as high-dimensional multivariate data, functional data, and random graphs. Despite their favorable theoretical properties, the integration of depth measures into regression modeling to provide prediction regions remains a largely underexplored area of research. To address this gap, we propose a novel, model-free uncertainty quantification algorithm based on conditional depth measures--specifically, conditional kernel mean embeddings and an integrated depth measure. These new algorithms can be used to define prediction and tolerance regions when predictors and responses are defined in separable Hilbert spaces. The use of kernel mean embeddings ensures faster convergence rates in prediction region estimation. To enhance the practical utility of the algorithms with finite samples, we also introduce a conformal prediction variant that provides marginal, non-asymptotic guarantees for the derived prediction regions. Additionally, we establish both conditional and unconditional consistency results, as well as fast convergence rates in certain homoscedastic settings. We evaluate the finite--sample performance of our model in extensive simulation studies involving various types of functional data and traditional Euclidean scenarios. Finally, we demonstrate the practical relevance of our approach through a digital health application related to physical activity, aiming to provide personalized recommendations

Risk Bounds For Distributional Regression

This work examines risk bounds for nonparametric distributional regression estimators. For convex-constrained distributional regression, general upper bounds are established for the continuous ranked probability score (CRPS) and the worst-case mean squared error (MSE) across the domain. These theoretical results are applied to isotonic and trend filtering distributional regression, yielding convergence rates consistent with those for mean estimation. Furthermore, a general upper bound is derived for distributional regression under non-convex constraints, with a specific application to neural network-based estimators. Comprehensive experiments on both simulated and real data validate the theoretical contributions, demonstrating their practical effectiveness.

Confidence Interval Construction and Conditional Variance Estimation with Dense ReLU Networks

This paper addresses the problems of conditional variance estimation and confidence interval construction in nonparametric regression using dense networks with the Rectified Linear Unit (ReLU) activation function. We present a residual-based framework for conditional variance estimation, deriving nonasymptotic bounds for variance estimation under both heteroscedastic and homoscedastic settings. We relax the sub-Gaussian noise assumption, allowing the proposed bounds to accommodate sub-Exponential noise and beyond. Building on this, for a ReLU neural network estimator, we derive non-asymptotic bounds for both its conditional mean and variance estimation, representing the first result for variance estimation using ReLU networks. Furthermore, we develop a ReLU network based robust bootstrap procedure (Efron, 1992) for constructing confidence intervals for the true mean that comes with a theoretical guarantee on the coverage, providing a significant advancement in uncertainty quantification and the construction of reliable confidence intervals in deep learning settings.

Dense ReLU Neural Networks for Temporal-spatial Model

In this paper, we focus on fully connected deep neural networks utilizing the Rectified Linear Unit (ReLU) activation function for nonparametric estimation. We derive non-asymptotic bounds that lead to convergence rates, addressing both temporal and spatial dependence in the observed measurements. By accounting for dependencies across time and space, our models better reflect the complexities of real-world data, enhancing both predictive performance and theoretical robustness. We also tackle the curse of dimensionality by modeling the data on a manifold, exploring the intrinsic dimensionality of high-dimensional data. We broaden existing theoretical findings of temporal-spatial analysis by applying them to neural networks in more general contexts and demonstrate that our proof techniques are effective for models with short-range dependence. Our empirical simulations across various synthetic response functions underscore the superior performance of our method, outperforming established approaches in the existing literature. These findings provide valuable insights into the strong capabilities of dense neural networks for temporal-spatial modeling across a broad range of function classes.

Statistical Guarantees for Lifelong Reinforcement Learning using PAC-Bayesian Theory

Lifelong reinforcement learning (RL) has been developed as a paradigm for extending single-task RL to more realistic, dynamic settings. In lifelong RL, the "life" of an RL agent is modeled as a stream of tasks drawn from a task distribution. We propose EPIC (\underline{E}mpirical \underline{P}AC-Bayes that \underline{I}mproves \underline{C}ontinuously), a novel algorithm designed for lifelong RL using PAC-Bayes theory. EPIC learns a shared policy distribution, referred to as the \textit{world policy}, which enables rapid adaptation to new tasks while retaining valuable knowledge from previous experiences. Our theoretical analysis establishes a relationship between the algorithm's generalization performance and the number of prior tasks preserved in memory. We also derive the sample complexity of EPIC in terms of RL regret. Extensive experiments on a variety of environments demonstrate that EPIC significantly outperforms existing methods in lifelong RL, offering both theoretical guarantees and practical efficacy through the use of the world policy.

Network two-sample test for block models

We consider the two-sample testing problem for networks, where the goal is to determine whether two sets of networks originated from the same stochastic model. Assuming no vertex correspondence and allowing for different numbers of nodes, we address a fundamental network testing problem that goes beyond simple adjacency matrix comparisons. We adopt the stochastic block model (SBM) for network distributions, due to their interpretability and the potential to approximate more general models. The lack of meaningful node labels and vertex correspondence translate to a graph matching challenge when developing a test for SBMs. We introduce an efficient algorithm to match estimated network parameters, allowing us to properly combine and contrast information within and across samples, leading to a powerful test. We show that the matching algorithm, and the overall test are consistent, under mild conditions on the sparsity of the networks and the sample sizes, and derive a chi-squared asymptotic null distribution for the test. Through a mixture of theoretical insights and empirical validations, including experiments with both synthetic and real-world data, this study advances robust statistical inference for complex network data.

kNN Algorithm for Conditional Mean and Variance Estimation with Automated Uncertainty Quantification and Variable Selection

In this paper, we introduce a kNN-based regression method that synergizes the scalability and adaptability of traditional non-parametric kNN models with a novel variable selection technique. This method focuses on accurately estimating the conditional mean and variance of random response variables, thereby effectively characterizing conditional distributions across diverse scenarios.Our approach incorporates a robust uncertainty quantification mechanism, leveraging our prior estimation work on conditional mean and variance. The employment of kNN ensures scalable computational efficiency in predicting intervals and statistical accuracy in line with optimal non-parametric rates. Additionally, we introduce a new kNN semi-parametric algorithm for estimating ROC curves, accounting for covariates. For selecting the smoothing parameter k, we propose an algorithm with theoretical guarantees.Incorporation of variable selection enhances the performance of the method significantly over conventional kNN techniques in various modeling tasks. We validate the approach through simulations in low, moderate, and high-dimensional covariate spaces. The algorithm's effectiveness is particularly notable in biomedical applications as demonstrated in two case studies. Concluding with a theoretical analysis, we highlight the consistency and convergence rate of our method over traditional kNN models, particularly when the underlying regression model takes values in a low-dimensional space.

Temporal-spatial model via Trend Filtering

This research focuses on the estimation of a non-parametric regression function designed for data with simultaneous time and space dependencies. In such a context, we study the Trend Filtering, a nonparametric estimator introduced by \cite{mammen1997locally} and \cite{rudin1992nonlinear}. For univariate settings, the signals we consider are assumed to have a kth weak derivative with bounded total variation, allowing for a general degree of smoothness. In the multivariate scenario, we study a $K$-Nearest Neighbor fused lasso estimator as in \cite{padilla2018adaptive}, employing an ADMM algorithm, suitable for signals with bounded variation that adhere to a piecewise Lipschitz continuity criterion. By aligning with lower bounds, the minimax optimality of our estimators is validated. A unique phase transition phenomenon, previously uncharted in Trend Filtering studies, emerges through our analysis. Both Simulation studies and real data applications underscore the superior performance of our method when compared with established techniques in the existing literature.

Kernel Biclustering algorithm in Hilbert Spaces

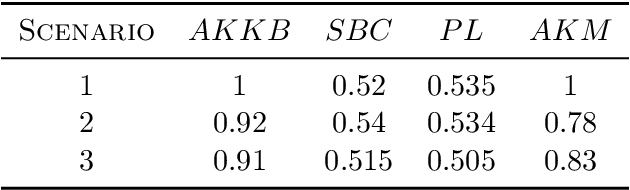
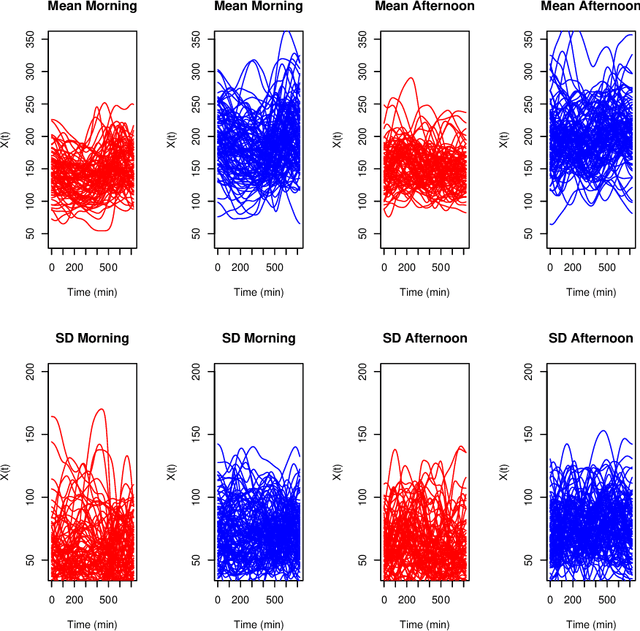
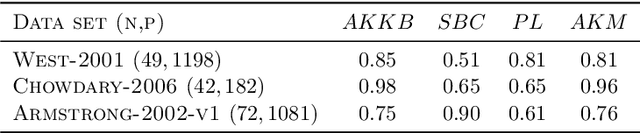
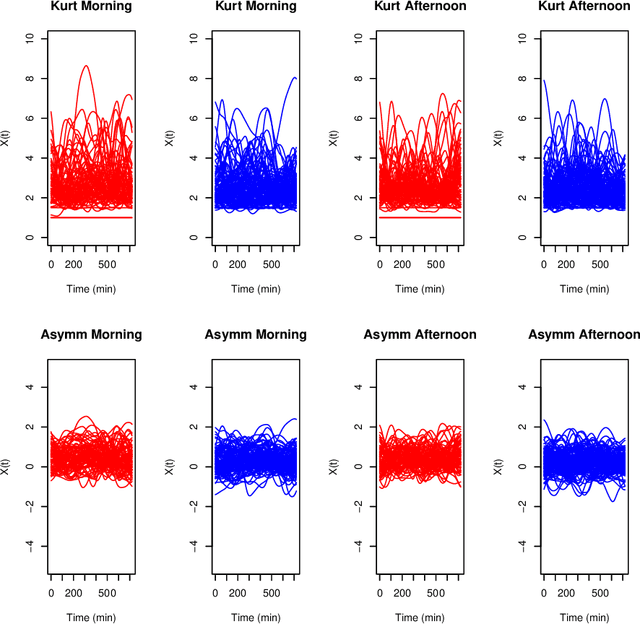
Biclustering algorithms partition data and covariates simultaneously, providing new insights in several domains, such as analyzing gene expression to discover new biological functions. This paper develops a new model-free biclustering algorithm in abstract spaces using the notions of energy distance (ED) and the maximum mean discrepancy (MMD) -- two distances between probability distributions capable of handling complex data such as curves or graphs. The proposed method can learn more general and complex cluster shapes than most existing literature approaches, which usually focus on detecting mean and variance differences. Although the biclustering configurations of our approach are constrained to create disjoint structures at the datum and covariate levels, the results are competitive. Our results are similar to state-of-the-art methods in their optimal scenarios, assuming a proper kernel choice, outperforming them when cluster differences are concentrated in higher-order moments. The model's performance has been tested in several situations that involve simulated and real-world datasets. Finally, new theoretical consistency results are established using some tools of the theory of optimal transport.

Variance estimation in graphs with the fused lasso

We study the problem of variance estimation in general graph-structured problems. First, we develop a linear time estimator for the homoscedastic case that can consistently estimate the variance in general graphs. We show that our estimator attains minimax rates for the chain and 2D grid graphs when the mean signal has a total variation with canonical scaling. Furthermore, we provide general upper bounds on the mean squared error performance of the fused lasso estimator in general graphs under a moment condition and a bound on the tail behavior of the errors. These upper bounds allow us to generalize for broader classes of distributions, such as sub-Exponential, many existing results on the fused lasso that are only known to hold with the assumption that errors are sub-Gaussian random variables. Exploiting our upper bounds, we then study a simple total variation regularization estimator for estimating the signal of variances in the heteroscedastic case. Our results show that the variance estimator attains minimax rates for estimating signals of bounded variation in grid graphs, $K$-nearest neighbor graphs with very mild assumptions, and it is consistent for estimating the variances in any connected graph. In addition, extensive numerical results show that our proposed estimators perform reasonably well in a variety of graph-structured models.