Expressive power of tensor-network factorizations for probabilistic modeling, with applications from hidden Markov models to quantum machine learning
Paper and Code
Jul 08, 2019
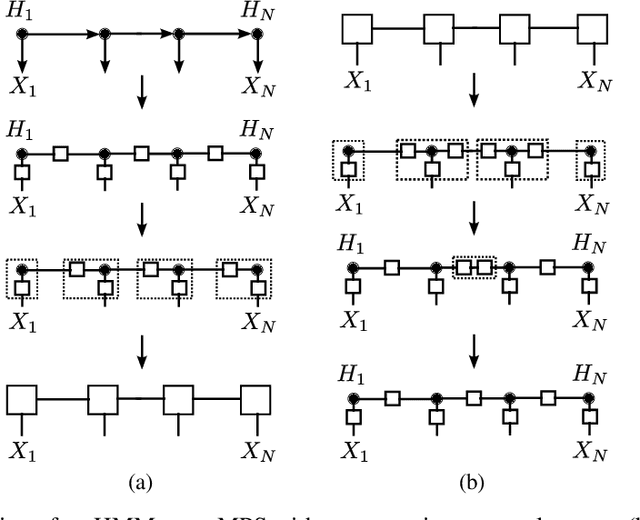
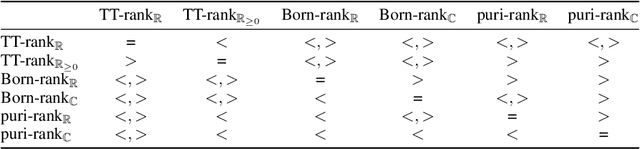
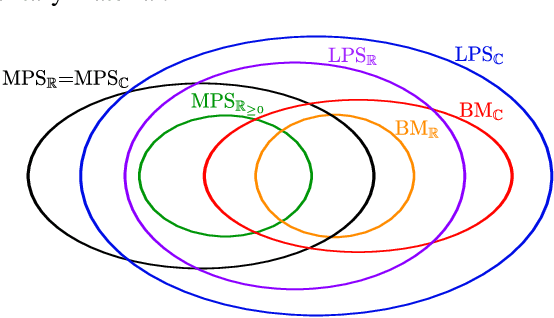
Tensor-network techniques have enjoyed outstanding success in physics, and have recently attracted attention in machine learning, both as a tool for the formulation of new learning algorithms and for enhancing the mathematical understanding of existing methods. Inspired by these developments, and the natural correspondence between tensor networks and probabilistic graphical models, we provide a rigorous analysis of the expressive power of various tensor-network factorizations of discrete multivariate probability distributions. These factorizations include non-negative tensor-trains/MPS, which are in correspondence with hidden Markov models, and Born machines, which are naturally related to local quantum circuits. When used to model probability distributions, they exhibit tractable likelihoods and admit efficient learning algorithms. Interestingly, we prove that there exist probability distributions for which there are unbounded separations between the resource requirements of some of these tensor-network factorizations. Particularly surprising is the fact that using complex instead of real tensors can lead to an arbitrarily large reduction in the number of parameters of the network. Additionally, we introduce locally purified states (LPS), a new factorization inspired by techniques for the simulation of quantum systems, with provably better expressive power than all other representations considered. The ramifications of this result are explored through numerical experiments. Our findings imply that LPS should be considered over hidden Markov models, and furthermore provide guidelines for the design of local quantum circuits for probabilistic modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge