Taking gradients through experiments: LSTMs and memory proximal policy optimization for black-box quantum control

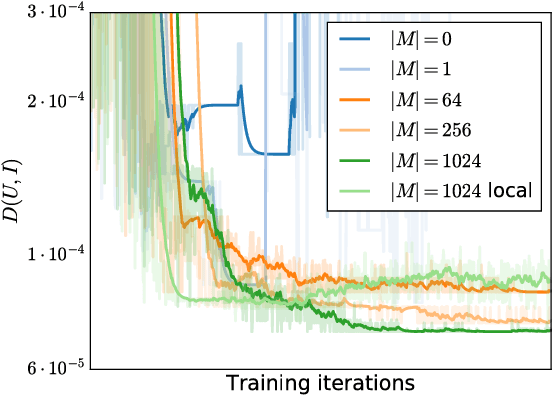
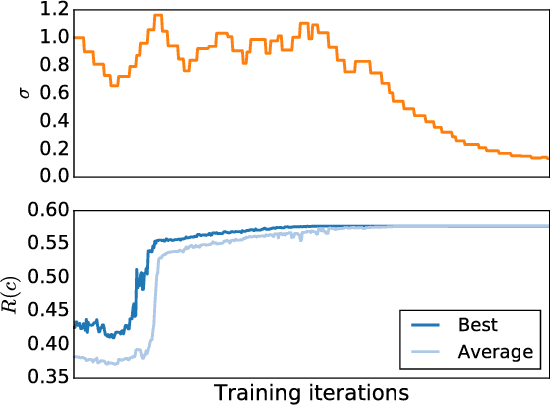
In this work we introduce the application of black-box quantum control as an interesting rein- forcement learning problem to the machine learning community. We analyze the structure of the reinforcement learning problems arising in quantum physics and argue that agents parameterized by long short-term memory (LSTM) networks trained via stochastic policy gradients yield a general method to solving them. In this context we introduce a variant of the proximal policy optimization (PPO) algorithm called the memory proximal policy optimization (MPPO) which is based on this analysis. We then show how it can be applied to specific learning tasks and present results of nu- merical experiments showing that our method achieves state-of-the-art results for several learning tasks in quantum control with discrete and continouous control parameters.

Neural-Network Quantum States, String-Bond States, and Chiral Topological States

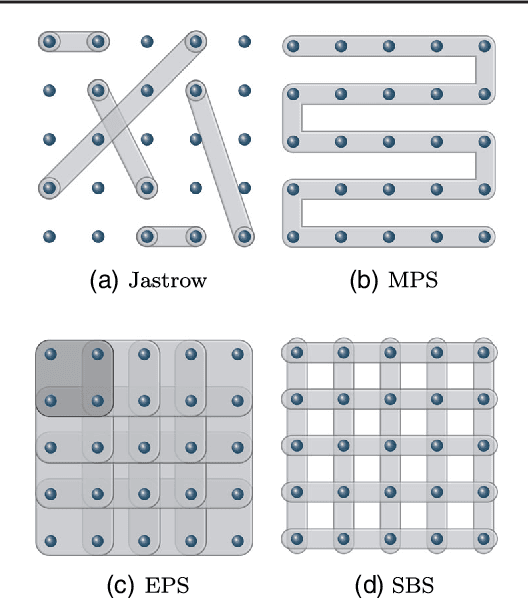
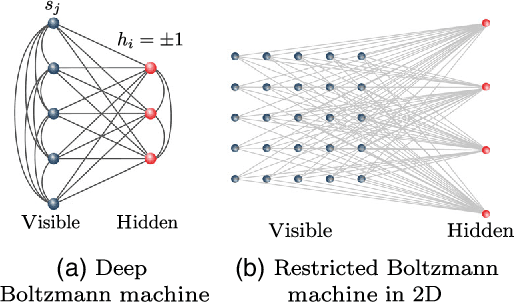
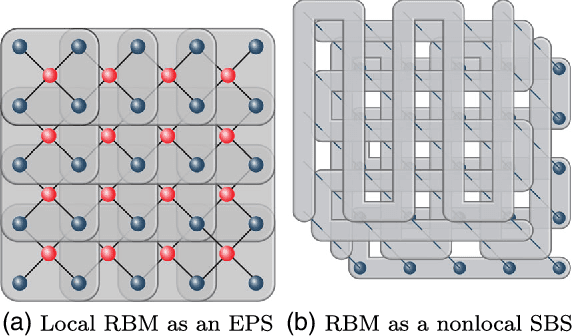
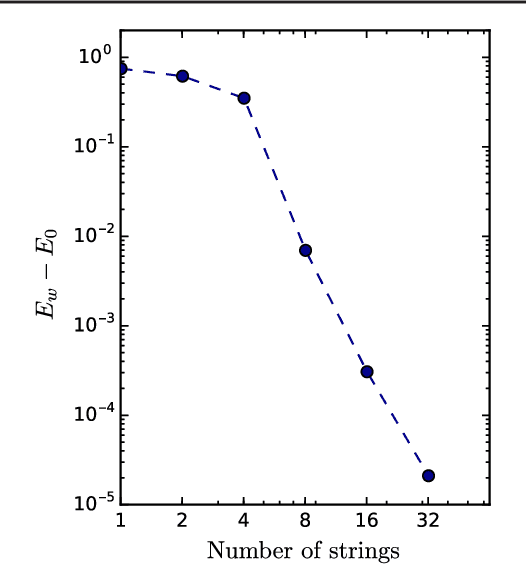
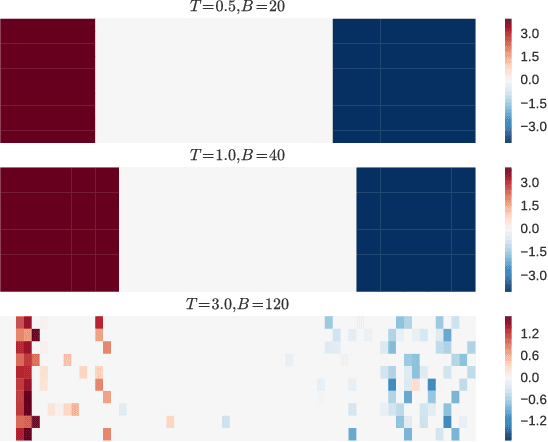
Neural-Network Quantum States have been recently introduced as an Ansatz for describing the wave function of quantum many-body systems. We show that there are strong connections between Neural-Network Quantum States in the form of Restricted Boltzmann Machines and some classes of Tensor-Network states in arbitrary dimensions. In particular we demonstrate that short-range Restricted Boltzmann Machines are Entangled Plaquette States, while fully connected Restricted Boltzmann Machines are String-Bond States with a nonlocal geometry and low bond dimension. These results shed light on the underlying architecture of Restricted Boltzmann Machines and their efficiency at representing many-body quantum states. String-Bond States also provide a generic way of enhancing the power of Neural-Network Quantum States and a natural generalization to systems with larger local Hilbert space. We compare the advantages and drawbacks of these different classes of states and present a method to combine them together. This allows us to benefit from both the entanglement structure of Tensor Networks and the efficiency of Neural-Network Quantum States into a single Ansatz capable of targeting the wave function of strongly correlated systems. While it remains a challenge to describe states with chiral topological order using traditional Tensor Networks, we show that Neural-Network Quantum States and their String-Bond States extension can describe a lattice Fractional Quantum Hall state exactly. In addition, we provide numerical evidence that Neural-Network Quantum States can approximate a chiral spin liquid with better accuracy than Entangled Plaquette States and local String-Bond States. Our results demonstrate the efficiency of neural networks to describe complex quantum wave functions and pave the way towards the use of String-Bond States as a tool in more traditional machine-learning applications.

Using Recurrent Neural Networks to Optimize Dynamical Decoupling for Quantum Memory

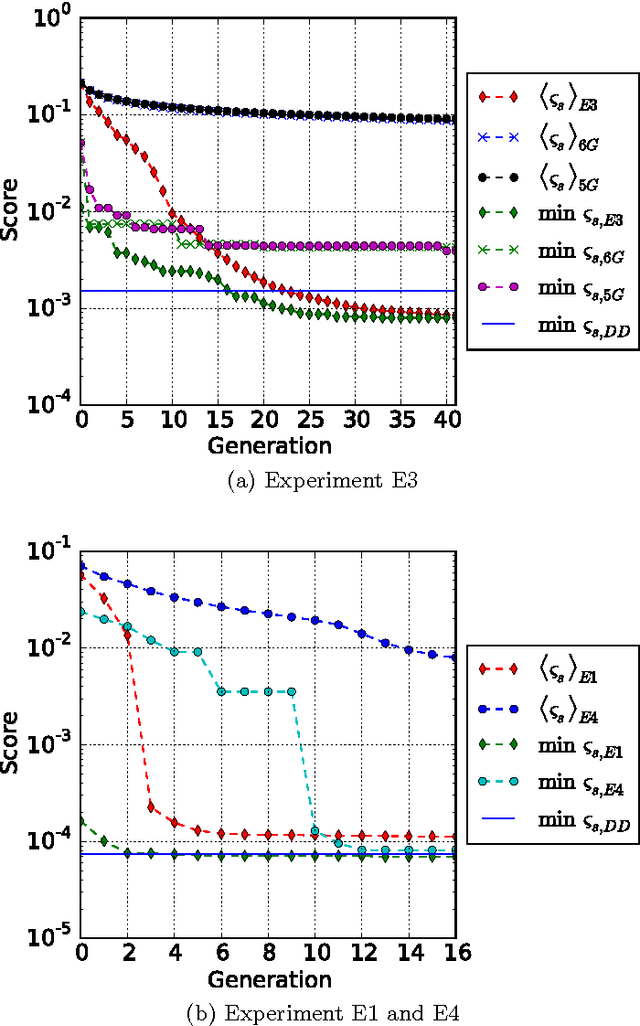
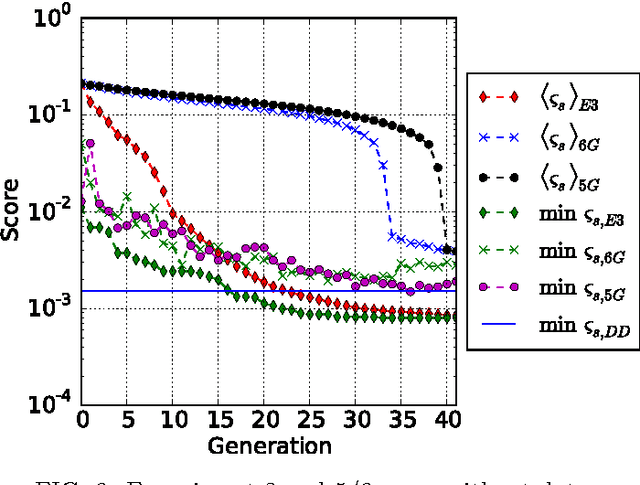
We utilize machine learning models which are based on recurrent neural networks to optimize dynamical decoupling (DD) sequences. DD is a relatively simple technique for suppressing the errors in quantum memory for certain noise models. In numerical simulations, we show that with minimum use of prior knowledge and starting from random sequences, the models are able to improve over time and eventually output DD-sequences with performance better than that of the well known DD-families. Furthermore, our algorithm is easy to implement in experiments to find solutions tailored to the specific hardware, as it treats the figure of merit as a black box.