Learning First-Order Representations for Planning from Black-Box States: New Results

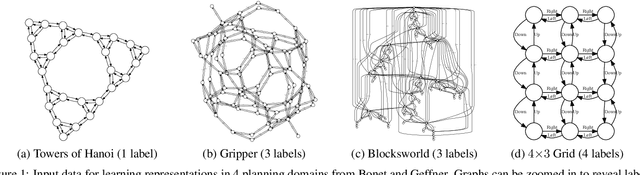
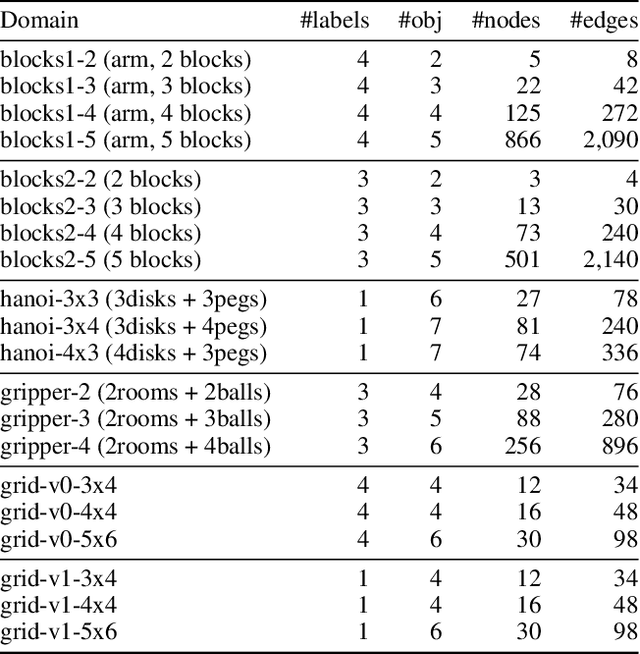
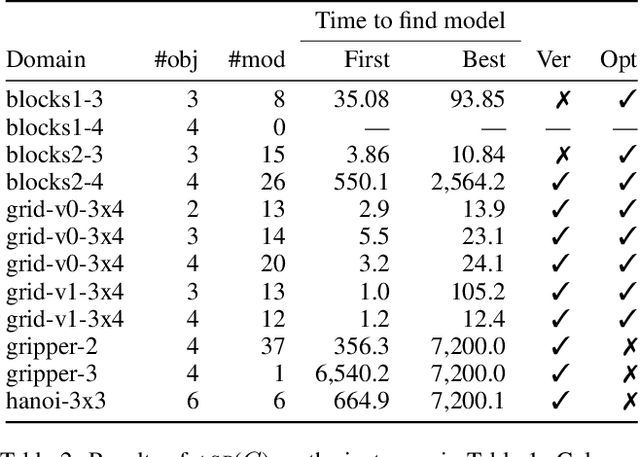
Recently Bonet and Geffner have shown that first-order representations for planning domains can be learned from the structure of the state space without any prior knowledge about the action schemas or domain predicates. For this, the learning problem is formulated as the search for a simplest first-order domain description D that along with information about instances I_i (number of objects and initial state) determine state space graphs G(P_i) that match the observed state graphs G_i where P_i = (D, I_i). The search is cast and solved approximately by means of a SAT solver that is called over a large family of propositional theories that differ just in the parameters encoding the possible number of action schemas and domain predicates, their arities, and the number of objects. In this work, we push the limits of these learners by moving to an answer set programming (ASP) encoding using the CLINGO system. The new encodings are more transparent and concise, extending the range of possible models while facilitating their exploration. We show that the domains introduced by Bonet and Geffner can be solved more efficiently in the new approach, often optimally, and furthermore, that the approach can be easily extended to handle partial information about the state graphs as well as noise that prevents some states from being distinguished.

Flexible FOND Planning with Explicit Fairness Assumptions

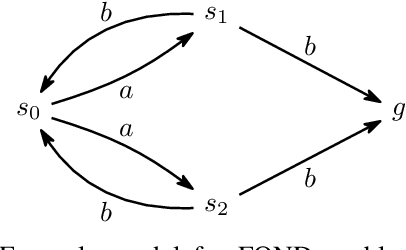
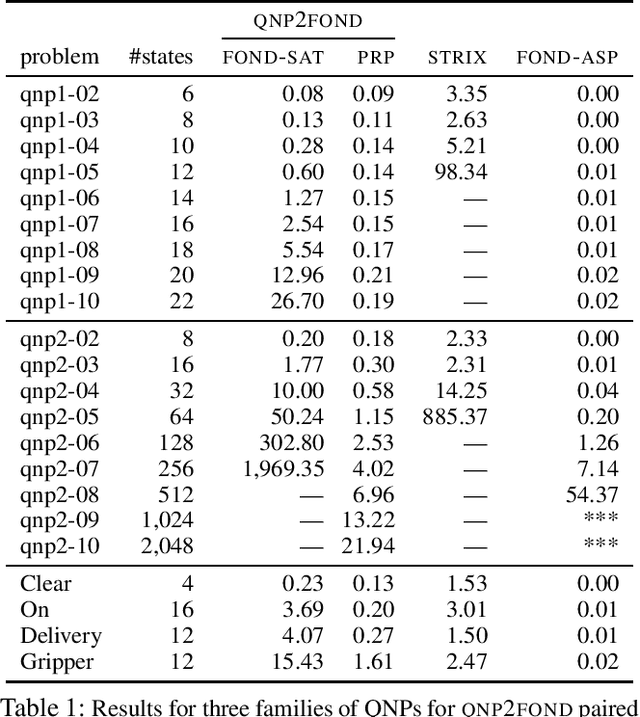
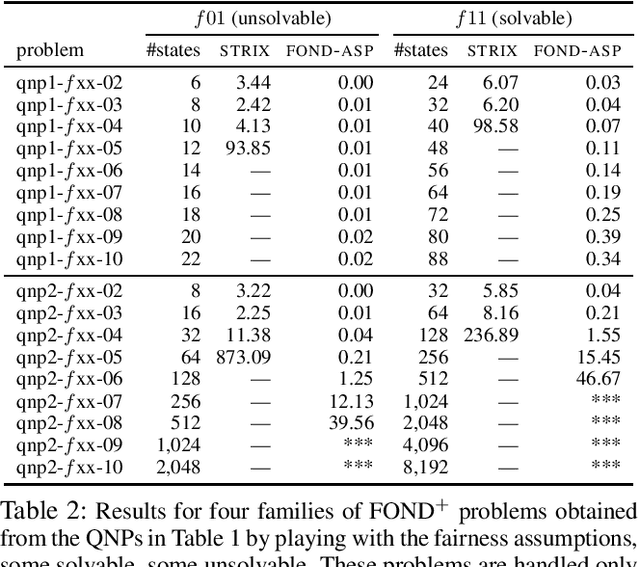
We consider the problem of reaching a propositional goal condition in fully-observable non-deterministic (FOND) planning under a general class of fairness assumptions that are given explicitly. The fairness assumptions are of the form A/B and say that state trajectories that contain infinite occurrences of an action a from A in a state s and finite occurrence of actions from B, must also contain infinite occurrences of action a in s followed by each one of its possible outcomes. The infinite trajectories that violate this condition are deemed as unfair, and the solutions are policies for which all the fair trajectories reach a goal state. We show that strong and strong-cyclic FOND planning, as well as QNP planning, a planning model introduced recently for generalized planning, are all special cases of FOND planning with fairness assumptions of this form which can also be combined. FOND+ planning, as this form of planning is called, combines the syntax of FOND planning with some of the versatility of LTL for expressing fairness constraints. A new planner is implemented by reducing FOND+ planning to answer set programs, and the performance of the planner is evaluated in comparison with FOND and QNP planners, and LTL synthesis tools.

Neural-Network Quantum States, String-Bond States, and Chiral Topological States

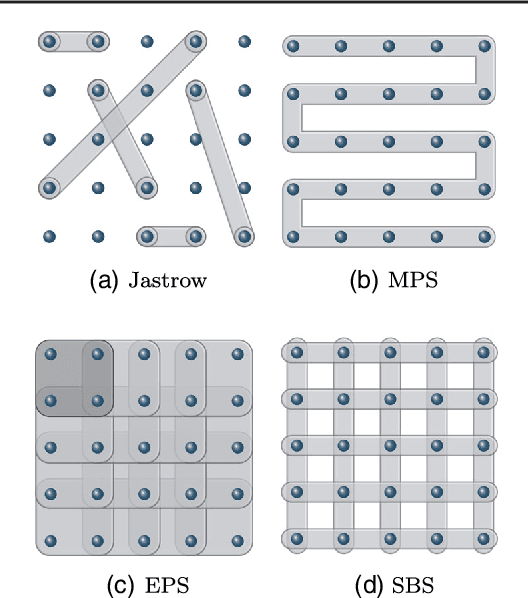
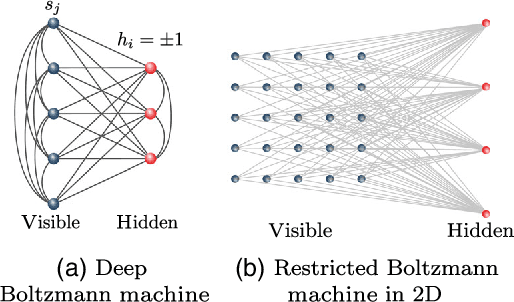
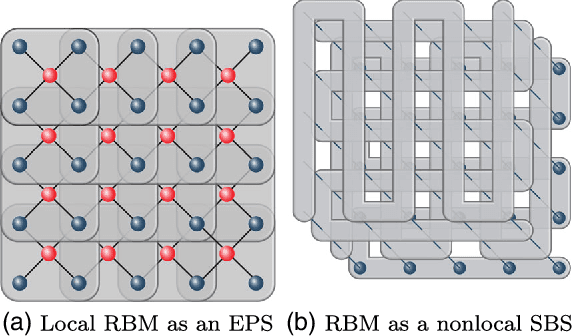
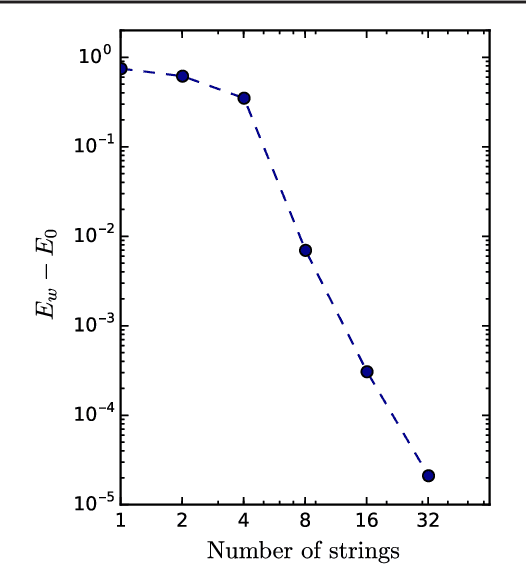
Neural-Network Quantum States have been recently introduced as an Ansatz for describing the wave function of quantum many-body systems. We show that there are strong connections between Neural-Network Quantum States in the form of Restricted Boltzmann Machines and some classes of Tensor-Network states in arbitrary dimensions. In particular we demonstrate that short-range Restricted Boltzmann Machines are Entangled Plaquette States, while fully connected Restricted Boltzmann Machines are String-Bond States with a nonlocal geometry and low bond dimension. These results shed light on the underlying architecture of Restricted Boltzmann Machines and their efficiency at representing many-body quantum states. String-Bond States also provide a generic way of enhancing the power of Neural-Network Quantum States and a natural generalization to systems with larger local Hilbert space. We compare the advantages and drawbacks of these different classes of states and present a method to combine them together. This allows us to benefit from both the entanglement structure of Tensor Networks and the efficiency of Neural-Network Quantum States into a single Ansatz capable of targeting the wave function of strongly correlated systems. While it remains a challenge to describe states with chiral topological order using traditional Tensor Networks, we show that Neural-Network Quantum States and their String-Bond States extension can describe a lattice Fractional Quantum Hall state exactly. In addition, we provide numerical evidence that Neural-Network Quantum States can approximate a chiral spin liquid with better accuracy than Entangled Plaquette States and local String-Bond States. Our results demonstrate the efficiency of neural networks to describe complex quantum wave functions and pave the way towards the use of String-Bond States as a tool in more traditional machine-learning applications.