Label-free Prediction of Vascular Connectivity in Perfused Microvascular Networks in vitro

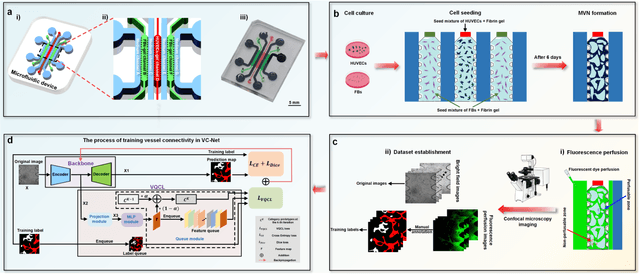
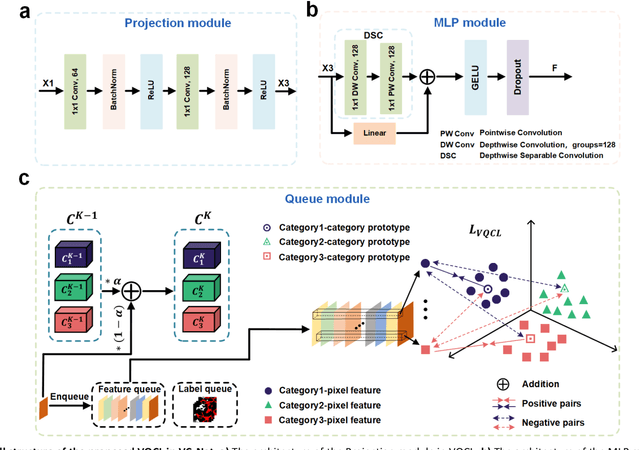
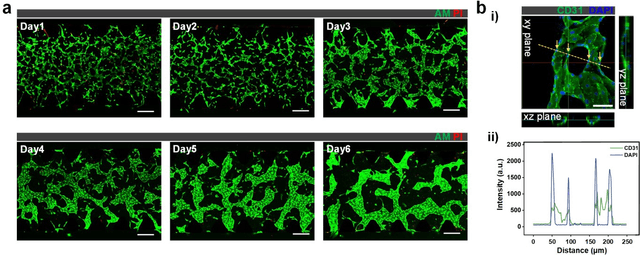
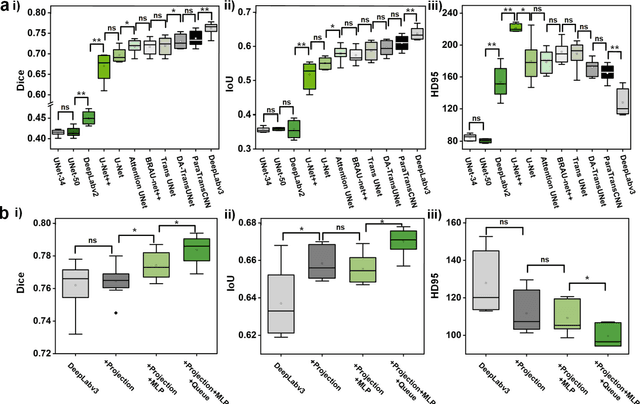
Continuous monitoring and in-situ assessment of microvascular connectivity have significant implications for culturing vascularized organoids and optimizing the therapeutic strategies. However, commonly used methods for vascular connectivity assessment heavily rely on fluorescent labels that may either raise biocompatibility concerns or interrupt the normal cell growth process. To address this issue, a Vessel Connectivity Network (VC-Net) was developed for label-free assessment of vascular connectivity. To validate the VC-Net, microvascular networks (MVNs) were cultured in vitro and their microscopic images were acquired at different culturing conditions as a training dataset. The VC-Net employs a Vessel Queue Contrastive Learning (VQCL) method and a class imbalance algorithm to address the issues of limited sample size, indistinctive class features and imbalanced class distribution in the dataset. The VC-Net successfully evaluated the vascular connectivity with no significant deviation from that by fluorescence imaging. In addition, the proposed VC-Net successfully differentiated the connectivity characteristics between normal and tumor-related MVNs. In comparison with those cultured in the regular microenvironment, the averaged connectivity of MVNs cultured in the tumor-related microenvironment decreased by 30.8%, whereas the non-connected area increased by 37.3%. This study provides a new avenue for label-free and continuous assessment of organoid or tumor vascularization in vitro.

AquilaMoE: Efficient Training for MoE Models with Scale-Up and Scale-Out Strategies

In recent years, with the rapid application of large language models across various fields, the scale of these models has gradually increased, and the resources required for their pre-training have grown exponentially. Training an LLM from scratch will cost a lot of computation resources while scaling up from a smaller model is a more efficient approach and has thus attracted significant attention. In this paper, we present AquilaMoE, a cutting-edge bilingual 8*16B Mixture of Experts (MoE) language model that has 8 experts with 16 billion parameters each and is developed using an innovative training methodology called EfficientScale. This approach optimizes performance while minimizing data requirements through a two-stage process. The first stage, termed Scale-Up, initializes the larger model with weights from a pre-trained smaller model, enabling substantial knowledge transfer and continuous pretraining with significantly less data. The second stage, Scale-Out, uses a pre-trained dense model to initialize the MoE experts, further enhancing knowledge transfer and performance. Extensive validation experiments on 1.8B and 7B models compared various initialization schemes, achieving models that maintain and reduce loss during continuous pretraining. Utilizing the optimal scheme, we successfully trained a 16B model and subsequently the 8*16B AquilaMoE model, demonstrating significant improvements in performance and training efficiency.

Improving the List Decoding Version of the Cyclically Equivariant Neural Decoder

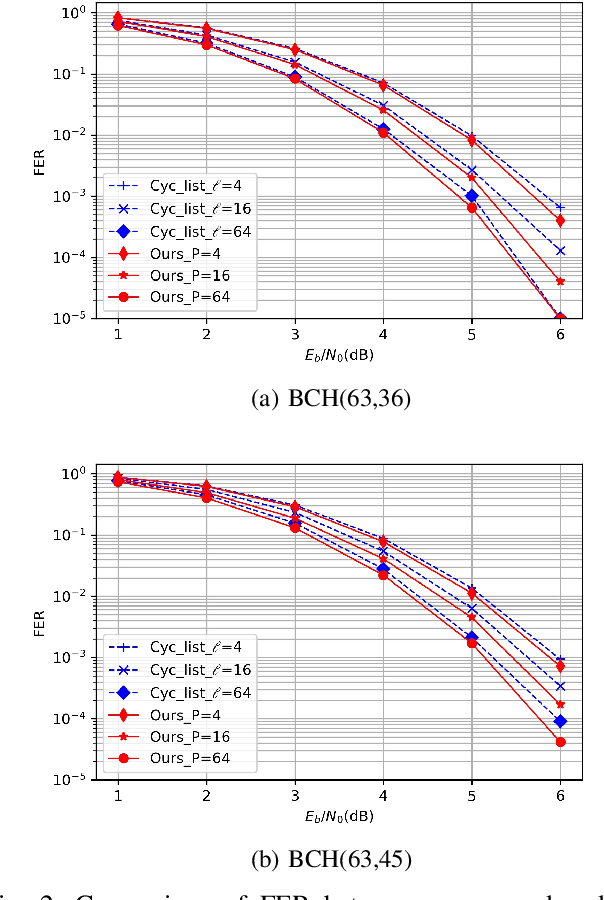
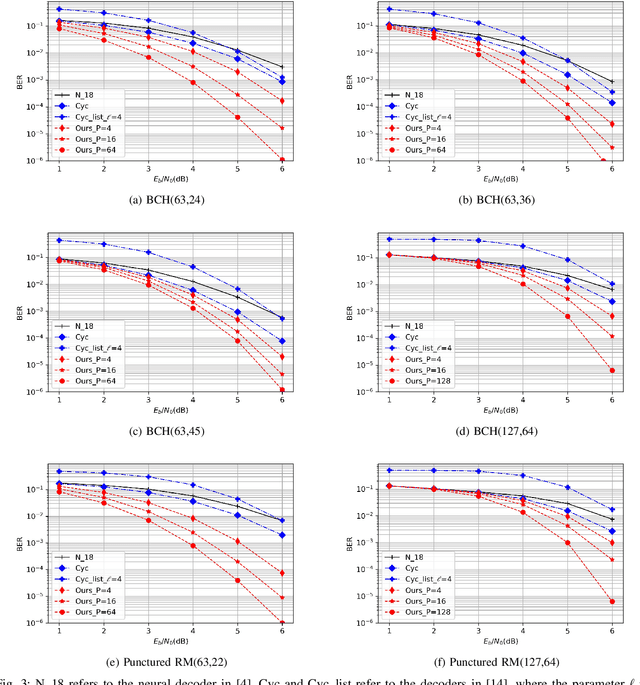
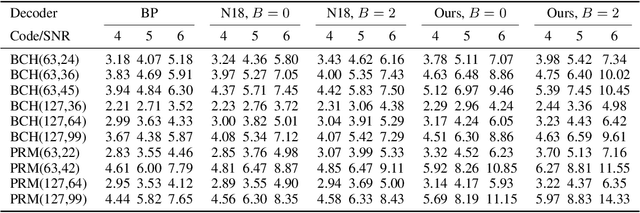
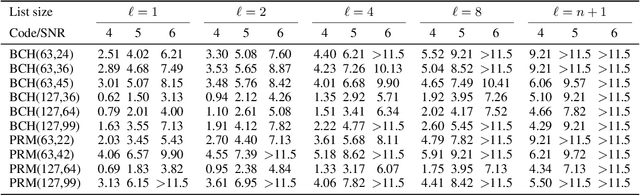
The cyclically equivariant neural decoder was recently proposed in [Chen-Ye, International Conference on Machine Learning, 2021] to decode cyclic codes. In the same paper, a list decoding procedure was also introduced for two widely used classes of cyclic codes -- BCH codes and punctured Reed-Muller (RM) codes. While the list decoding procedure significantly improves the Frame Error Rate (FER) of the cyclically equivariant neural decoder, the Bit Error Rate (BER) of the list decoding procedure is even worse than the unique decoding algorithm when the list size is small. In this paper, we propose an improved version of the list decoding algorithm for BCH codes and punctured RM codes. Our new proposal significantly reduces the BER while maintaining the same (in some cases even smaller) FER. More specifically, our new decoder provides up to $2$dB gain over the previous list decoder when measured by BER, and the running time of our new decoder is $15\%$ smaller. Code available at https://github.com/improvedlistdecoder/code

Cyclically Equivariant Neural Decoders for Cyclic Codes

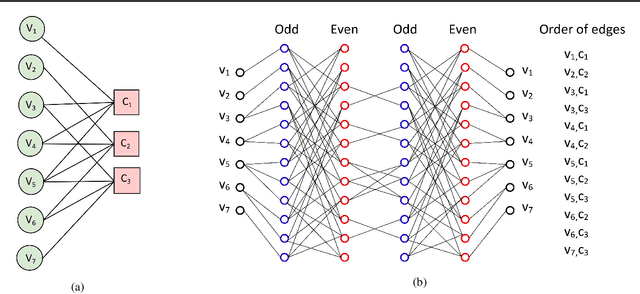
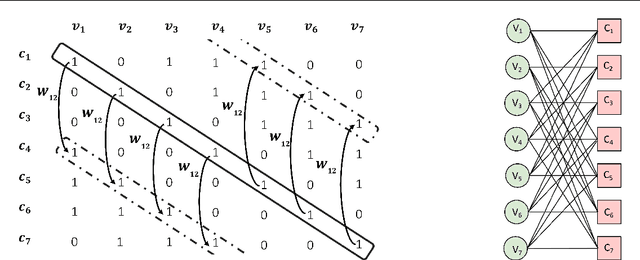
Neural decoders were introduced as a generalization of the classic Belief Propagation (BP) decoding algorithms, where the Trellis graph in the BP algorithm is viewed as a neural network, and the weights in the Trellis graph are optimized by training the neural network. In this work, we propose a novel neural decoder for cyclic codes by exploiting their cyclically invariant property. More precisely, we impose a shift invariant structure on the weights of our neural decoder so that any cyclic shift of inputs results in the same cyclic shift of outputs. Extensive simulations with BCH codes and punctured Reed-Muller (RM) codes show that our new decoder consistently outperforms previous neural decoders when decoding cyclic codes. Finally, we propose a list decoding procedure that can significantly reduce the decoding error probability for BCH codes and punctured RM codes. For certain high-rate codes, the gap between our list decoder and the Maximum Likelihood decoder is less than $0.1$dB. Code available at https://github.com/cyclicallyneuraldecoder/CyclicallyEquivariantNeuralDecoders

Exact recovery and sharp thresholds of Stochastic Ising Block Model

The stochastic block model (SBM) is a random graph model in which the edges are generated according to the underlying cluster structure on the vertices. The (ferromagnetic) Ising model, on the other hand, assigns $\pm 1$ labels to vertices according to an underlying graph structure in a way that if two vertices are connected in the graph then they are more likely to be assigned the same label. In SBM, one aims to recover the underlying clusters from the graph structure while in Ising model, an extensively-studied problem is to recover the underlying graph structure based on i.i.d. samples (labelings of the vertices). In this paper, we propose a natural composition of SBM and the Ising model, which we call the Stochastic Ising Block Model (SIBM). In SIBM, we take SBM in its simplest form, where $n$ vertices are divided into two equal-sized clusters and the edges are connected independently with probability $p$ within clusters and $q$ across clusters. Then we use the graph $G$ generated by the SBM as the underlying graph of the Ising model and draw $m$ i.i.d. samples from it. The objective is to exactly recover the two clusters in SBM from the samples generated by the Ising model, without observing the graph $G$. As the main result of this paper, we establish a sharp threshold $m^\ast$ on the sample complexity of this exact recovery problem in a properly chosen regime, where $m^\ast$ can be calculated from the parameters of SIBM. We show that when $m\ge m^\ast$, one can recover the clusters from $m$ samples in $O(n)$ time as the number of vertices $n$ goes to infinity. When $m<m^\ast$, we further show that for almost all choices of parameters of SIBM, the success probability of any recovery algorithms approaches $0$ as $n\to\infty$.

Optimal locally private estimation under $\ell_p$ loss for $1\le p\le 2$

We consider the minimax estimation problem of a discrete distribution with support size $k$ under locally differential privacy constraints. A privatization scheme is applied to each raw sample independently, and we need to estimate the distribution of the raw samples from the privatized samples. A positive number $\epsilon$ measures the privacy level of a privatization scheme. In our previous work (IEEE Trans. Inform. Theory, 2018), we proposed a family of new privatization schemes and the corresponding estimator. We also proved that our scheme and estimator are order optimal in the regime $e^{\epsilon} \ll k$ under both $\ell_2^2$ (mean square) and $\ell_1$ loss. In this paper, we sharpen this result by showing asymptotic optimality of the proposed scheme under the $\ell_p^p$ loss for all $1\le p\le 2.$ More precisely, we show that for any $p\in[1,2]$ and any $k$ and $\epsilon,$ the ratio between the worst-case $\ell_p^p$ estimation loss of our scheme and the optimal value approaches $1$ as the number of samples tends to infinity. The lower bound on the minimax risk of private estimation that we establish as a part of the proof is valid for any loss function $\ell_p^p, p\ge 1.$

Communication-Computation Efficient Gradient Coding

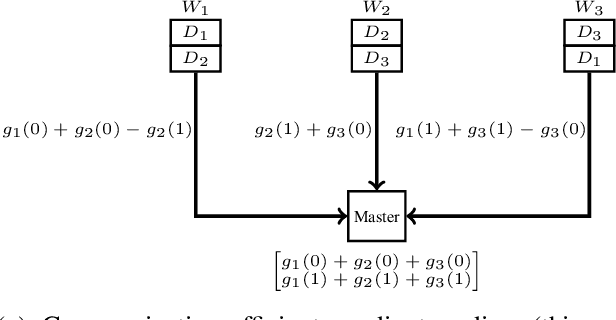
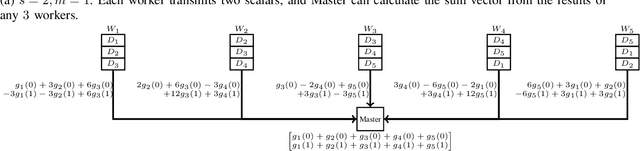
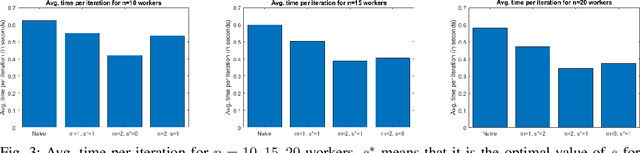
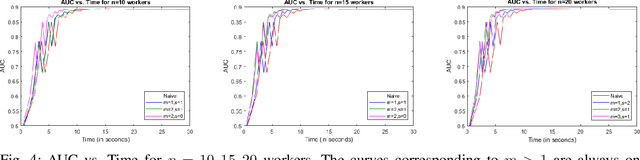
This paper develops coding techniques to reduce the running time of distributed learning tasks. It characterizes the fundamental tradeoff to compute gradients (and more generally vector summations) in terms of three parameters: computation load, straggler tolerance and communication cost. It further gives an explicit coding scheme that achieves the optimal tradeoff based on recursive polynomial constructions, coding both across data subsets and vector components. As a result, the proposed scheme allows to minimize the running time for gradient computations. Implementations are made on Amazon EC2 clusters using Python with mpi4py package. Results show that the proposed scheme maintains the same generalization error while reducing the running time by $32\%$ compared to uncoded schemes and $23\%$ compared to prior coded schemes focusing only on stragglers (Tandon et al., ICML 2017).

Asymptotically optimal private estimation under mean square loss

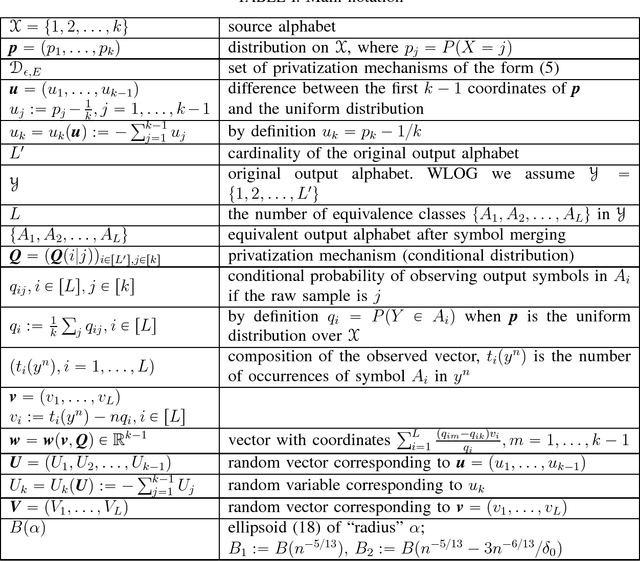
We consider the minimax estimation problem of a discrete distribution with support size $k$ under locally differential privacy constraints. A privatization scheme is applied to each raw sample independently, and we need to estimate the distribution of the raw samples from the privatized samples. A positive number $\epsilon$ measures the privacy level of a privatization scheme. In our previous work (arXiv:1702.00610), we proposed a family of new privatization schemes and the corresponding estimator. We also proved that our scheme and estimator are order optimal in the regime $e^{\epsilon} \ll k$ under both $\ell_2^2$ and $\ell_1$ loss. In other words, for a large number of samples the worst-case estimation loss of our scheme was shown to differ from the optimal value by at most a constant factor. In this paper, we eliminate this gap by showing asymptotic optimality of the proposed scheme and estimator under the $\ell_2^2$ (mean square) loss. More precisely, we show that for any $k$ and $\epsilon,$ the ratio between the worst-case estimation loss of our scheme and the optimal value approaches $1$ as the number of samples tends to infinity.

Optimal Schemes for Discrete Distribution Estimation under Locally Differential Privacy

We consider the minimax estimation problem of a discrete distribution with support size $k$ under privacy constraints. A privatization scheme is applied to each raw sample independently, and we need to estimate the distribution of the raw samples from the privatized samples. A positive number $\epsilon$ measures the privacy level of a privatization scheme. For a given $\epsilon,$ we consider the problem of constructing optimal privatization schemes with $\epsilon$-privacy level, i.e., schemes that minimize the expected estimation loss for the worst-case distribution. Two schemes in the literature provide order optimal performance in the high privacy regime where $\epsilon$ is very close to $0,$ and in the low privacy regime where $e^{\epsilon}\approx k,$ respectively. In this paper, we propose a new family of schemes which substantially improve the performance of the existing schemes in the medium privacy regime when $1\ll e^{\epsilon} \ll k.$ More concretely, we prove that when $3.8 < \epsilon <\ln(k/9) ,$ our schemes reduce the expected estimation loss by $50\%$ under $\ell_2^2$ metric and by $30\%$ under $\ell_1$ metric over the existing schemes. We also prove a lower bound for the region $e^{\epsilon} \ll k,$ which implies that our schemes are order optimal in this regime.