Optimal locally private estimation under $\ell_p$ loss for $1\le p\le 2$

We consider the minimax estimation problem of a discrete distribution with support size $k$ under locally differential privacy constraints. A privatization scheme is applied to each raw sample independently, and we need to estimate the distribution of the raw samples from the privatized samples. A positive number $\epsilon$ measures the privacy level of a privatization scheme. In our previous work (IEEE Trans. Inform. Theory, 2018), we proposed a family of new privatization schemes and the corresponding estimator. We also proved that our scheme and estimator are order optimal in the regime $e^{\epsilon} \ll k$ under both $\ell_2^2$ (mean square) and $\ell_1$ loss. In this paper, we sharpen this result by showing asymptotic optimality of the proposed scheme under the $\ell_p^p$ loss for all $1\le p\le 2.$ More precisely, we show that for any $p\in[1,2]$ and any $k$ and $\epsilon,$ the ratio between the worst-case $\ell_p^p$ estimation loss of our scheme and the optimal value approaches $1$ as the number of samples tends to infinity. The lower bound on the minimax risk of private estimation that we establish as a part of the proof is valid for any loss function $\ell_p^p, p\ge 1.$

Asymptotically optimal private estimation under mean square loss

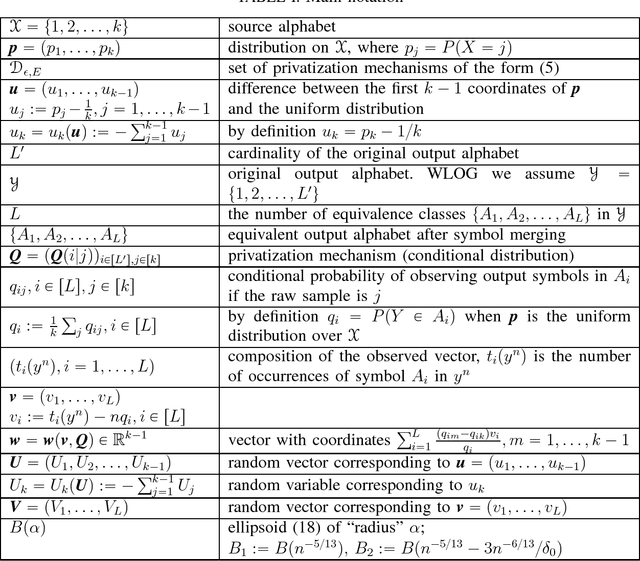
We consider the minimax estimation problem of a discrete distribution with support size $k$ under locally differential privacy constraints. A privatization scheme is applied to each raw sample independently, and we need to estimate the distribution of the raw samples from the privatized samples. A positive number $\epsilon$ measures the privacy level of a privatization scheme. In our previous work (arXiv:1702.00610), we proposed a family of new privatization schemes and the corresponding estimator. We also proved that our scheme and estimator are order optimal in the regime $e^{\epsilon} \ll k$ under both $\ell_2^2$ and $\ell_1$ loss. In other words, for a large number of samples the worst-case estimation loss of our scheme was shown to differ from the optimal value by at most a constant factor. In this paper, we eliminate this gap by showing asymptotic optimality of the proposed scheme and estimator under the $\ell_2^2$ (mean square) loss. More precisely, we show that for any $k$ and $\epsilon,$ the ratio between the worst-case estimation loss of our scheme and the optimal value approaches $1$ as the number of samples tends to infinity.

Optimal Schemes for Discrete Distribution Estimation under Locally Differential Privacy

We consider the minimax estimation problem of a discrete distribution with support size $k$ under privacy constraints. A privatization scheme is applied to each raw sample independently, and we need to estimate the distribution of the raw samples from the privatized samples. A positive number $\epsilon$ measures the privacy level of a privatization scheme. For a given $\epsilon,$ we consider the problem of constructing optimal privatization schemes with $\epsilon$-privacy level, i.e., schemes that minimize the expected estimation loss for the worst-case distribution. Two schemes in the literature provide order optimal performance in the high privacy regime where $\epsilon$ is very close to $0,$ and in the low privacy regime where $e^{\epsilon}\approx k,$ respectively. In this paper, we propose a new family of schemes which substantially improve the performance of the existing schemes in the medium privacy regime when $1\ll e^{\epsilon} \ll k.$ More concretely, we prove that when $3.8 < \epsilon <\ln(k/9) ,$ our schemes reduce the expected estimation loss by $50\%$ under $\ell_2^2$ metric and by $30\%$ under $\ell_1$ metric over the existing schemes. We also prove a lower bound for the region $e^{\epsilon} \ll k,$ which implies that our schemes are order optimal in this regime.