Robust Multi-Objective Bayesian Optimization Under Input Noise

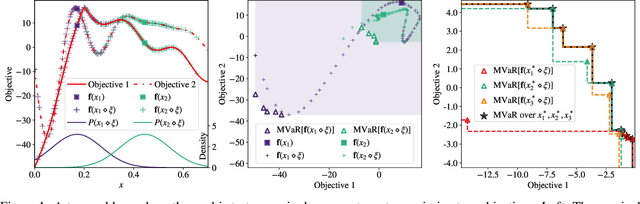
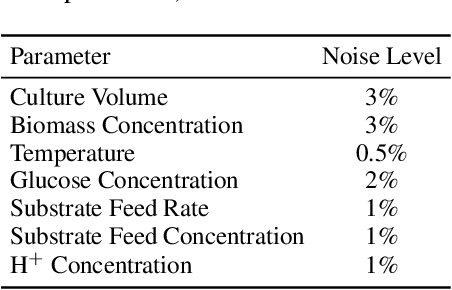
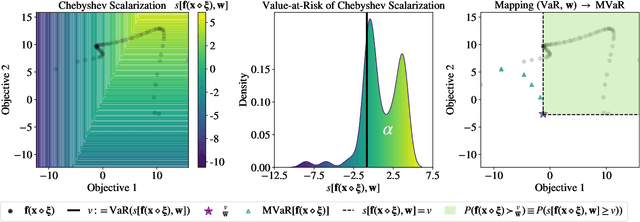
Bayesian optimization (BO) is a sample-efficient approach for tuning design parameters to optimize expensive-to-evaluate, black-box performance metrics. In many manufacturing processes, the design parameters are subject to random input noise, resulting in a product that is often less performant than expected. Although BO methods have been proposed for optimizing a single objective under input noise, no existing method addresses the practical scenario where there are multiple objectives that are sensitive to input perturbations. In this work, we propose the first multi-objective BO method that is robust to input noise. We formalize our goal as optimizing the multivariate value-at-risk (MVaR), a risk measure of the uncertain objectives. Since directly optimizing MVaR is computationally infeasible in many settings, we propose a scalable, theoretically-grounded approach for optimizing MVaR using random scalarizations. Empirically, we find that our approach significantly outperforms alternative methods and efficiently identifies optimal robust designs that will satisfy specifications across multiple metrics with high probability.

Adversarial Attacks on Graph Classification via Bayesian Optimisation

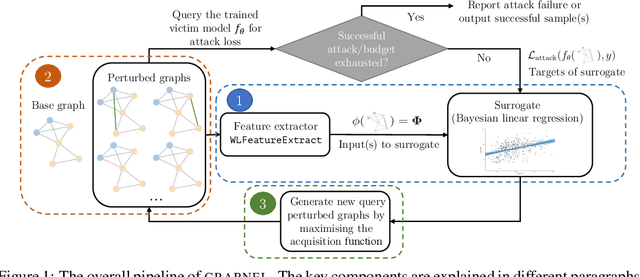
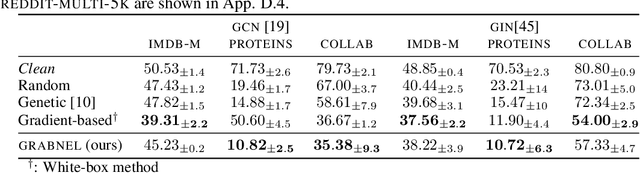
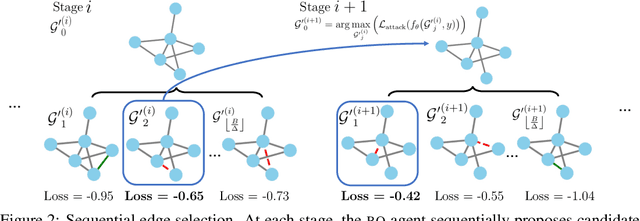
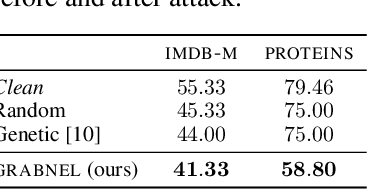
Graph neural networks, a popular class of models effective in a wide range of graph-based learning tasks, have been shown to be vulnerable to adversarial attacks. While the majority of the literature focuses on such vulnerability in node-level classification tasks, little effort has been dedicated to analysing adversarial attacks on graph-level classification, an important problem with numerous real-life applications such as biochemistry and social network analysis. The few existing methods often require unrealistic setups, such as access to internal information of the victim models, or an impractically-large number of queries. We present a novel Bayesian optimisation-based attack method for graph classification models. Our method is black-box, query-efficient and parsimonious with respect to the perturbation applied. We empirically validate the effectiveness and flexibility of the proposed method on a wide range of graph classification tasks involving varying graph properties, constraints and modes of attack. Finally, we analyse common interpretable patterns behind the adversarial samples produced, which may shed further light on the adversarial robustness of graph classification models.

Gaussian Process Sampling and Optimization with Approximate Upper and Lower Bounds

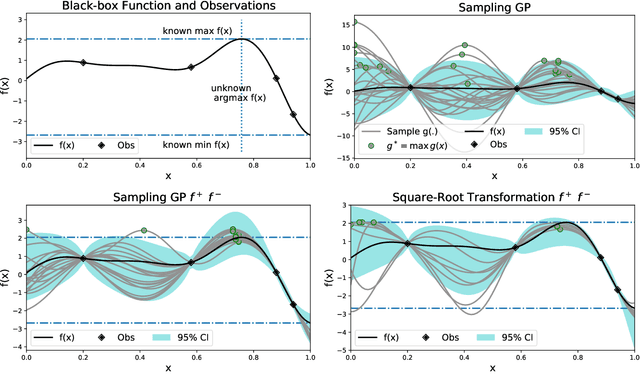
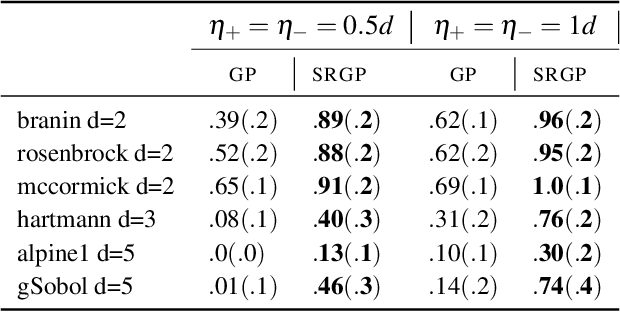
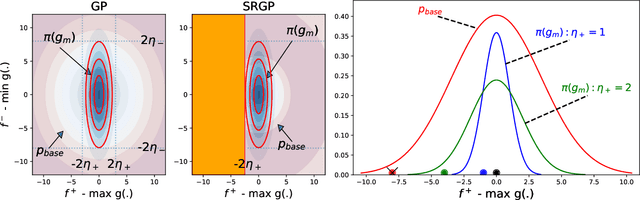
Many functions have approximately-known upper and/or lower bounds, potentially aiding the modeling of such functions. In this paper, we introduce Gaussian process models for functions where such bounds are (approximately) known. More specifically, we propose the first use of such bounds to improve Gaussian process (GP) posterior sampling and Bayesian optimization (BO). That is, we transform a GP model satisfying the given bounds, and then sample and weight functions from its posterior. To further exploit these bounds in BO settings, we present bounded entropy search (BES) to select the point gaining the most information about the underlying function, estimated by the GP samples, while satisfying the output constraints. We characterize the sample variance bounds and show that the decision made by BES is explainable. Our proposed approach is conceptually straightforward and can be used as a plug in extension to existing methods for GP posterior sampling and Bayesian optimization.

Revisiting Design Choices in Model-Based Offline Reinforcement Learning

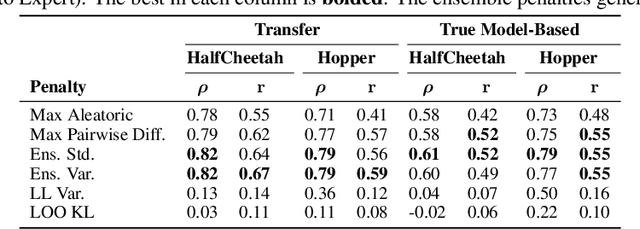
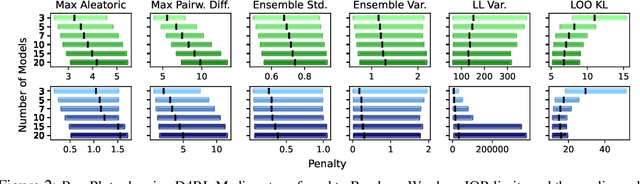
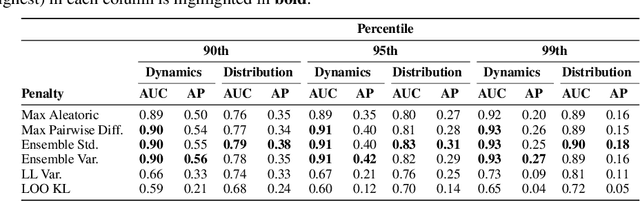
Offline reinforcement learning enables agents to leverage large pre-collected datasets of environment transitions to learn control policies, circumventing the need for potentially expensive or unsafe online data collection. Significant progress has been made recently in offline model-based reinforcement learning, approaches which leverage a learned dynamics model. This typically involves constructing a probabilistic model, and using the model uncertainty to penalize rewards where there is insufficient data, solving for a pessimistic MDP that lower bounds the true MDP. Existing methods, however, exhibit a breakdown between theory and practice, whereby pessimistic return ought to be bounded by the total variation distance of the model from the true dynamics, but is instead implemented through a penalty based on estimated model uncertainty. This has spawned a variety of uncertainty heuristics, with little to no comparison between differing approaches. In this paper, we compare these heuristics, and design novel protocols to investigate their interaction with other hyperparameters, such as the number of models, or imaginary rollout horizon. Using these insights, we show that selecting these key hyperparameters using Bayesian Optimization produces superior configurations that are vastly different to those currently used in existing hand-tuned state-of-the-art methods, and result in drastically stronger performance.

Universal Approximation of Functions on Sets

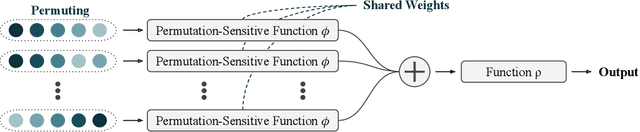
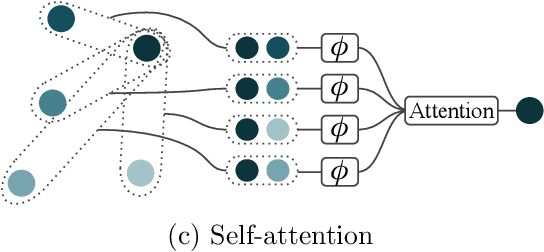
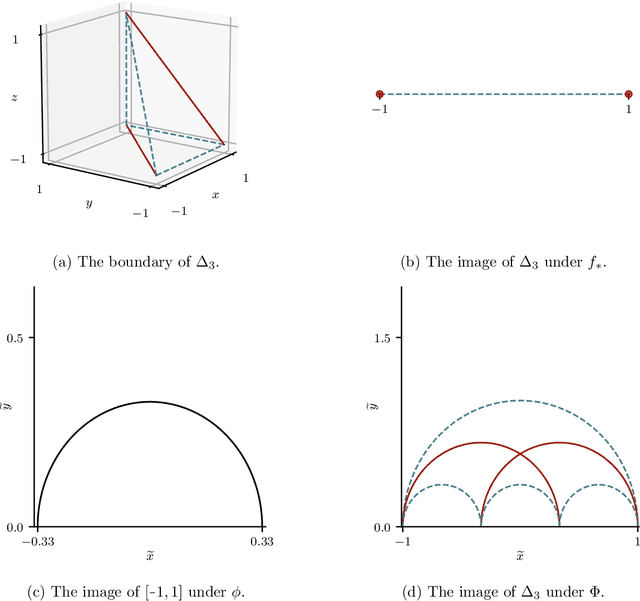
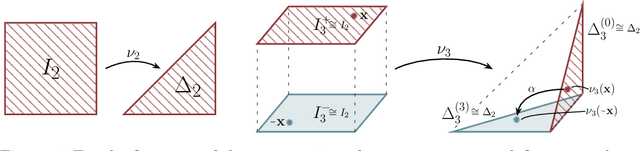
Modelling functions of sets, or equivalently, permutation-invariant functions, is a long-standing challenge in machine learning. Deep Sets is a popular method which is known to be a universal approximator for continuous set functions. We provide a theoretical analysis of Deep Sets which shows that this universal approximation property is only guaranteed if the model's latent space is sufficiently high-dimensional. If the latent space is even one dimension lower than necessary, there exist piecewise-affine functions for which Deep Sets performs no better than a na\"ive constant baseline, as judged by worst-case error. Deep Sets may be viewed as the most efficient incarnation of the Janossy pooling paradigm. We identify this paradigm as encompassing most currently popular set-learning methods. Based on this connection, we discuss the implications of our results for set learning more broadly, and identify some open questions on the universality of Janossy pooling in general.

Marginalising over Stationary Kernels with Bayesian Quadrature

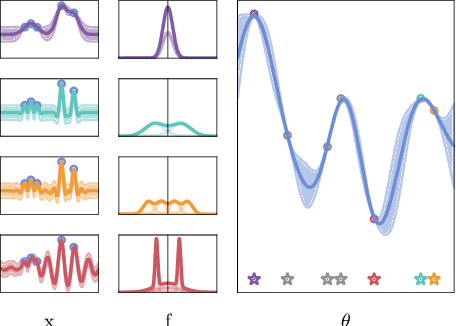
Marginalising over families of Gaussian Process kernels produces flexible model classes with well-calibrated uncertainty estimates. Existing approaches require likelihood evaluations of many kernels, rendering them prohibitively expensive for larger datasets. We propose a Bayesian Quadrature scheme to make this marginalisation more efficient and thereby more practical. Through use of the maximum mean discrepancies between distributions, we define a kernel over kernels that captures invariances between Spectral Mixture (SM) Kernels. Kernel samples are selected by generalising an information-theoretic acquisition function for warped Bayesian Quadrature. We show that our framework achieves more accurate predictions with better calibrated uncertainty than state-of-the-art baselines, especially when given limited (wall-clock) time budgets.

Think Global and Act Local: Bayesian Optimisation over High-Dimensional Categorical and Mixed Search Spaces

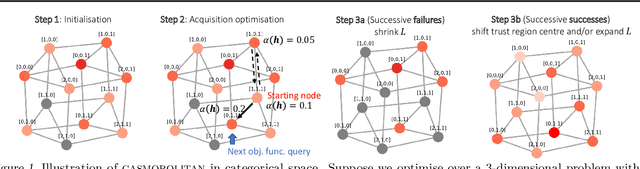
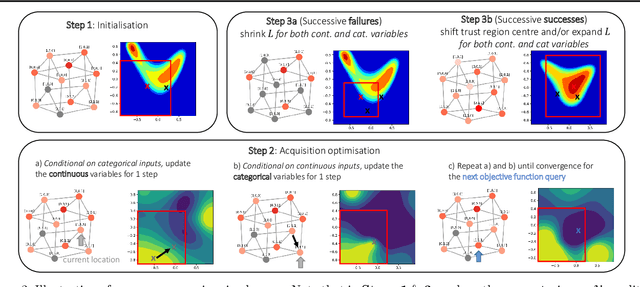
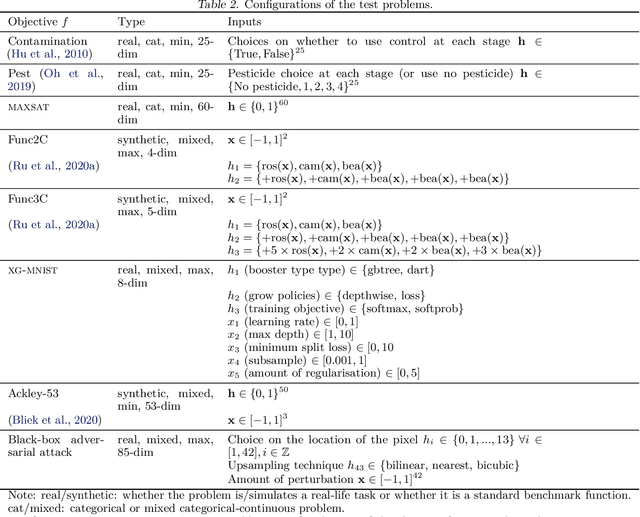
High-dimensional black-box optimisation remains an important yet notoriously challenging problem. Despite the success of Bayesian optimisation methods on continuous domains, domains that are categorical, or that mix continuous and categorical variables, remain challenging. We propose a novel solution -- we combine local optimisation with a tailored kernel design, effectively handling high-dimensional categorical and mixed search spaces, whilst retaining sample efficiency. We further derive convergence guarantee for the proposed approach. Finally, we demonstrate empirically that our method outperforms the current baselines on a variety of synthetic and real-world tasks in terms of performance, computational costs, or both.

Gaussian Process Bandit Optimization of the Thermodynamic Variational Objective

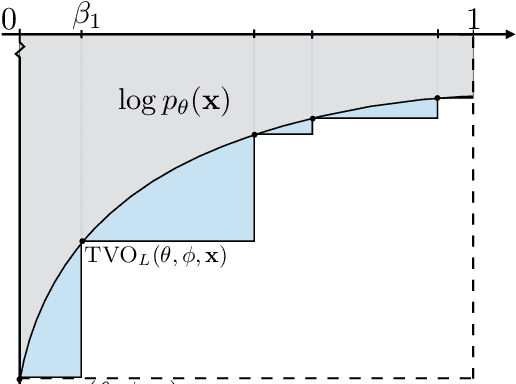
Achieving the full promise of the Thermodynamic Variational Objective (TVO), a recently proposed variational lower bound on the log evidence involving a one-dimensional Riemann integral approximation, requires choosing a "schedule" of sorted discretization points. This paper introduces a bespoke Gaussian process bandit optimization method for automatically choosing these points. Our approach not only automates their one-time selection, but also dynamically adapts their positions over the course of optimization, leading to improved model learning and inference. We provide theoretical guarantees that our bandit optimization converges to the regret-minimizing choice of integration points. Empirical validation of our algorithm is provided in terms of improved learning and inference in Variational Autoencoders and Sigmoid Belief Networks.

Adaptive Configuration Oracle for Online Portfolio Selection Methods

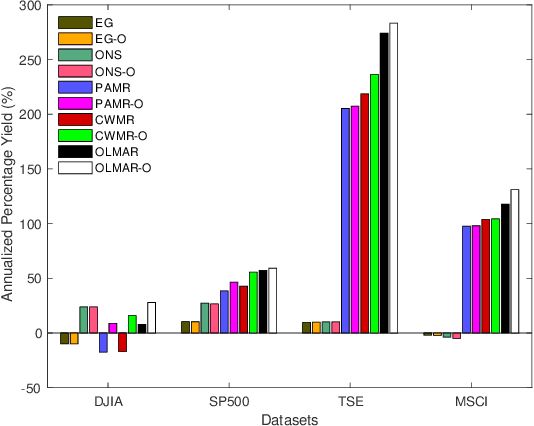
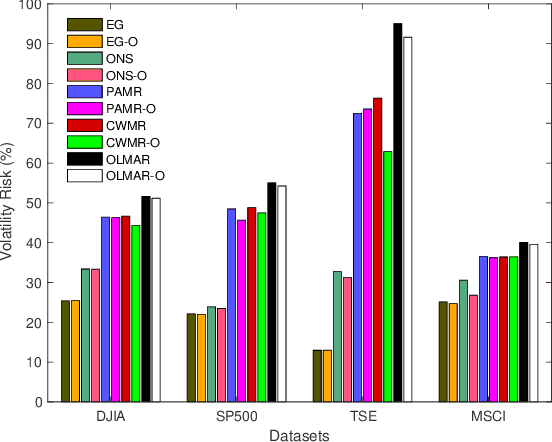
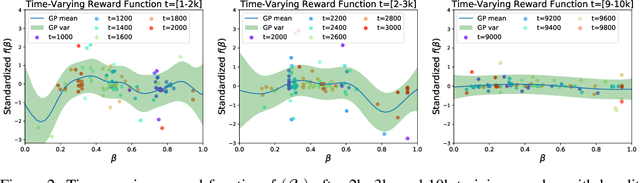
Financial markets are complex environments that produce enormous amounts of noisy and non-stationary data. One fundamental problem is online portfolio selection, the goal of which is to exploit this data to sequentially select portfolios of assets to achieve positive investment outcomes while managing risks. Various algorithms have been proposed for solving this problem in fields such as finance, statistics and machine learning, among others. Most of the methods have parameters that are estimated from backtests for good performance. Since these algorithms operate on non-stationary data that reflects the complexity of financial markets, we posit that adaptively tuning these parameters in an intelligent manner is a remedy for dealing with this complexity. In this paper, we model the mapping between the parameter space and the space of performance metrics using a Gaussian process prior. We then propose an oracle based on adaptive Bayesian optimization for automatically and adaptively configuring online portfolio selection methods. We test the efficacy of our solution on algorithms operating on equity and index data from various markets.

Bayesian Optimisation over Multiple Continuous and Categorical Inputs

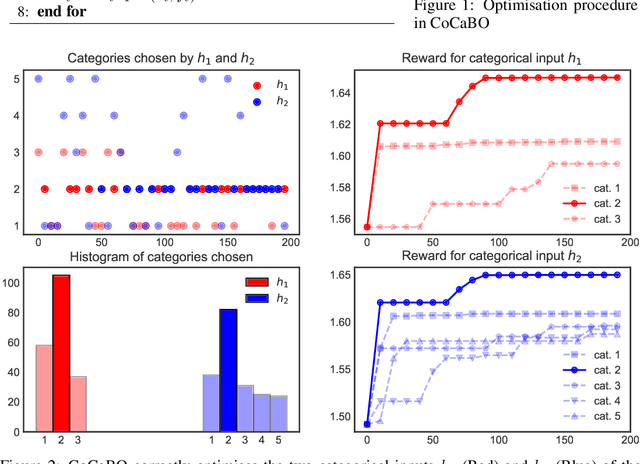
Efficient optimisation of black-box problems that comprise both continuous and categorical inputs is important, yet poses significant challenges. We propose a new approach, Continuous and Categorical Bayesian Optimisation (CoCaBO), which combines the strengths of multi-armed bandits and Bayesian optimisation to select values for both categorical and continuous inputs. We model this mixed-type space using a Gaussian Process kernel, designed to allow sharing of information across multiple categorical variables, each with multiple possible values; this allows CoCaBO to leverage all available data efficiently. We extend our method to the batch setting and propose an efficient selection procedure that dynamically balances exploration and exploitation whilst encouraging batch diversity. We demonstrate empirically that our method outperforms existing approaches on both synthetic and real-world optimisation tasks with continuous and categorical inputs.