Adaptive Configuration Oracle for Online Portfolio Selection Methods

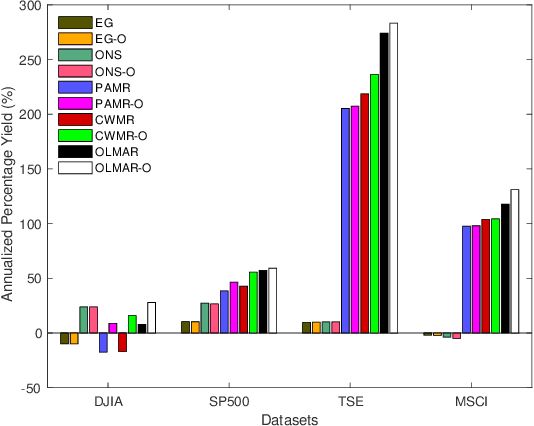
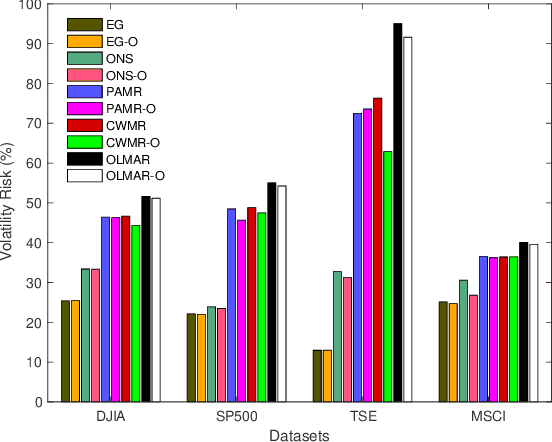
Financial markets are complex environments that produce enormous amounts of noisy and non-stationary data. One fundamental problem is online portfolio selection, the goal of which is to exploit this data to sequentially select portfolios of assets to achieve positive investment outcomes while managing risks. Various algorithms have been proposed for solving this problem in fields such as finance, statistics and machine learning, among others. Most of the methods have parameters that are estimated from backtests for good performance. Since these algorithms operate on non-stationary data that reflects the complexity of financial markets, we posit that adaptively tuning these parameters in an intelligent manner is a remedy for dealing with this complexity. In this paper, we model the mapping between the parameter space and the space of performance metrics using a Gaussian process prior. We then propose an oracle based on adaptive Bayesian optimization for automatically and adaptively configuring online portfolio selection methods. We test the efficacy of our solution on algorithms operating on equity and index data from various markets.

Bayesian Optimization for Dynamic Problems

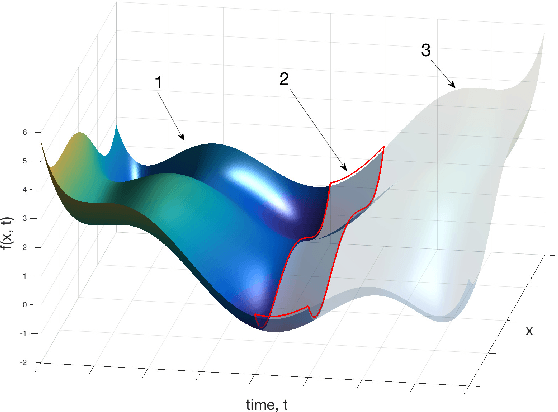
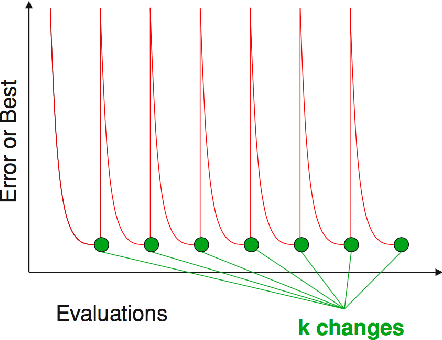
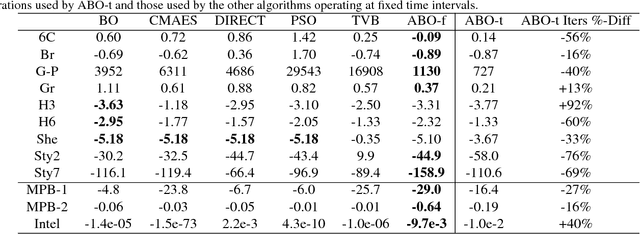
We propose practical extensions to Bayesian optimization for solving dynamic problems. We model dynamic objective functions using spatiotemporal Gaussian process priors which capture all the instances of the functions over time. Our extensions to Bayesian optimization use the information learnt from this model to guide the tracking of a temporally evolving minimum. By exploiting temporal correlations, the proposed method also determines when to make evaluations, how fast to make those evaluations, and it induces an appropriate budget of steps based on the available information. Lastly, we evaluate our technique on synthetic and real-world problems.