Expected Sliced Transport Plans

The optimal transport (OT) problem has gained significant traction in modern machine learning for its ability to: (1) provide versatile metrics, such as Wasserstein distances and their variants, and (2) determine optimal couplings between probability measures. To reduce the computational complexity of OT solvers, methods like entropic regularization and sliced optimal transport have been proposed. The sliced OT framework improves efficiency by comparing one-dimensional projections (slices) of high-dimensional distributions. However, despite their computational efficiency, sliced-Wasserstein approaches lack a transportation plan between the input measures, limiting their use in scenarios requiring explicit coupling. In this paper, we address two key questions: Can a transportation plan be constructed between two probability measures using the sliced transport framework? If so, can this plan be used to define a metric between the measures? We propose a "lifting" operation to extend one-dimensional optimal transport plans back to the original space of the measures. By computing the expectation of these lifted plans, we derive a new transportation plan, termed expected sliced transport (EST) plans. We prove that using the EST plan to weight the sum of the individual Euclidean costs for moving from one point to another results in a valid metric between the input discrete probability measures. We demonstrate the connection between our approach and the recently proposed min-SWGG, along with illustrative numerical examples that support our theoretical findings.

Manifold learning in Wasserstein space

This paper aims at building the theoretical foundations for manifold learning algorithms in the space of absolutely continuous probability measures on a compact and convex subset of $\mathbb{R}^d$, metrized with the Wasserstein-2 distance $W$. We begin by introducing a natural construction of submanifolds $\Lambda$ of probability measures equipped with metric $W_\Lambda$, the geodesic restriction of $W$ to $\Lambda$. In contrast to other constructions, these submanifolds are not necessarily flat, but still allow for local linearizations in a similar fashion to Riemannian submanifolds of $\mathbb{R}^d$. We then show how the latent manifold structure of $(\Lambda,W_{\Lambda})$ can be learned from samples $\{\lambda_i\}_{i=1}^N$ of $\Lambda$ and pairwise extrinsic Wasserstein distances $W$ only. In particular, we show that the metric space $(\Lambda,W_{\Lambda})$ can be asymptotically recovered in the sense of Gromov--Wasserstein from a graph with nodes $\{\lambda_i\}_{i=1}^N$ and edge weights $W(\lambda_i,\lambda_j)$. In addition, we demonstrate how the tangent space at a sample $\lambda$ can be asymptotically recovered via spectral analysis of a suitable "covariance operator" using optimal transport maps from $\lambda$ to sufficiently close and diverse samples $\{\lambda_i\}_{i=1}^N$. The paper closes with some explicit constructions of submanifolds $\Lambda$ and numerical examples on the recovery of tangent spaces through spectral analysis.

PT$\mathrm{L}^{p}$: Partial Transport $\mathrm{L}^{p}$ Distances

Optimal transport and its related problems, including optimal partial transport, have proven to be valuable tools in machine learning for computing meaningful distances between probability or positive measures. This success has led to a growing interest in defining transport-based distances that allow for comparing signed measures and, more generally, multi-channeled signals. Transport $\mathrm{L}^{p}$ distances are notable extensions of the optimal transport framework to signed and possibly multi-channeled signals. In this paper, we introduce partial transport $\mathrm{L}^{p}$ distances as a new family of metrics for comparing generic signals, benefiting from the robustness of partial transport distances. We provide theoretical background such as the existence of optimal plans and the behavior of the distance in various limits. Furthermore, we introduce the sliced variation of these distances, which allows for rapid comparison of generic signals. Finally, we demonstrate the application of the proposed distances in signal class separability and nearest neighbor classification.

Rates of Convergence for Regression with the Graph Poly-Laplacian

In the (special) smoothing spline problem one considers a variational problem with a quadratic data fidelity penalty and Laplacian regularisation. Higher order regularity can be obtained via replacing the Laplacian regulariser with a poly-Laplacian regulariser. The methodology is readily adapted to graphs and here we consider graph poly-Laplacian regularisation in a fully supervised, non-parametric, noise corrupted, regression problem. In particular, given a dataset $\{x_i\}_{i=1}^n$ and a set of noisy labels $\{y_i\}_{i=1}^n\subset\mathbb{R}$ we let $u_n:\{x_i\}_{i=1}^n\to\mathbb{R}$ be the minimiser of an energy which consists of a data fidelity term and an appropriately scaled graph poly-Laplacian term. When $y_i = g(x_i)+\xi_i$, for iid noise $\xi_i$, and using the geometric random graph, we identify (with high probability) the rate of convergence of $u_n$ to $g$ in the large data limit $n\to\infty$. Furthermore, our rate, up to logarithms, coincides with the known rate of convergence in the usual smoothing spline model.

Classification of datasets with imputed missing values: does imputation quality matter?

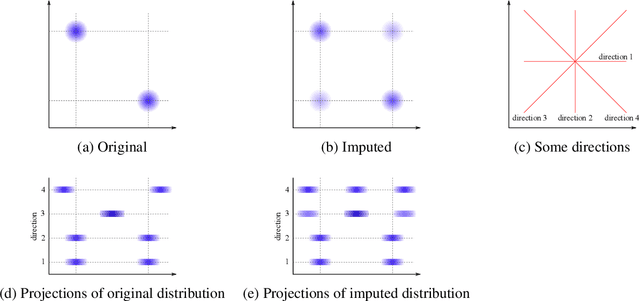
Classifying samples in incomplete datasets is a common aim for machine learning practitioners, but is non-trivial. Missing data is found in most real-world datasets and these missing values are typically imputed using established methods, followed by classification of the now complete, imputed, samples. The focus of the machine learning researcher is then to optimise the downstream classification performance. In this study, we highlight that it is imperative to consider the quality of the imputation. We demonstrate how the commonly used measures for assessing quality are flawed and propose a new class of discrepancy scores which focus on how well the method recreates the overall distribution of the data. To conclude, we highlight the compromised interpretability of classifier models trained using poorly imputed data.

Robust Certification for Laplace Learning on Geometric Graphs

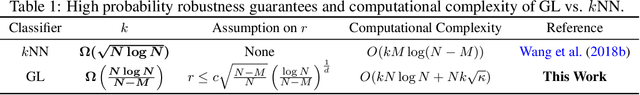
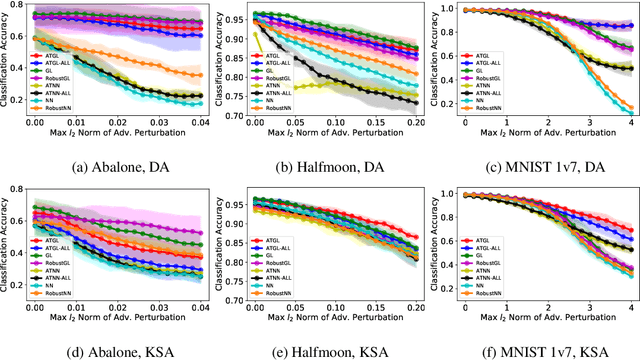
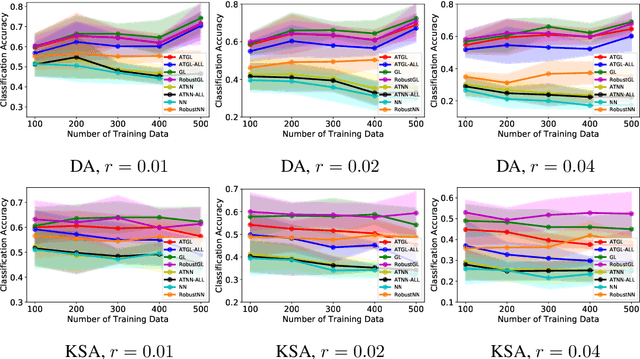
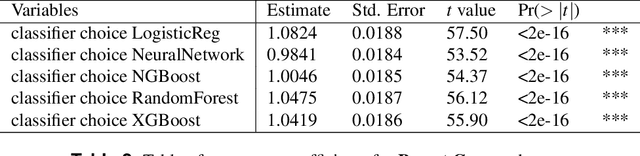
Graph Laplacian (GL)-based semi-supervised learning is one of the most used approaches for classifying nodes in a graph. Understanding and certifying the adversarial robustness of machine learning (ML) algorithms has attracted large amounts of attention from different research communities due to its crucial importance in many security-critical applied domains. There is great interest in the theoretical certification of adversarial robustness for popular ML algorithms. In this paper, we provide the first adversarial robust certification for the GL classifier. More precisely we quantitatively bound the difference in the classification accuracy of the GL classifier before and after an adversarial attack. Numerically, we validate our theoretical certification results and show that leveraging existing adversarial defenses for the $k$-nearest neighbor classifier can remarkably improve the robustness of the GL classifier.

A Linear Transportation $\mathrm{L}^p$ Distance for Pattern Recognition

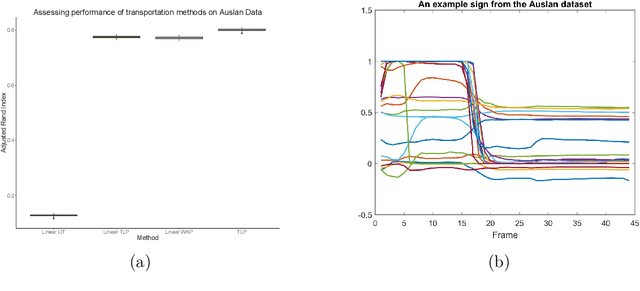
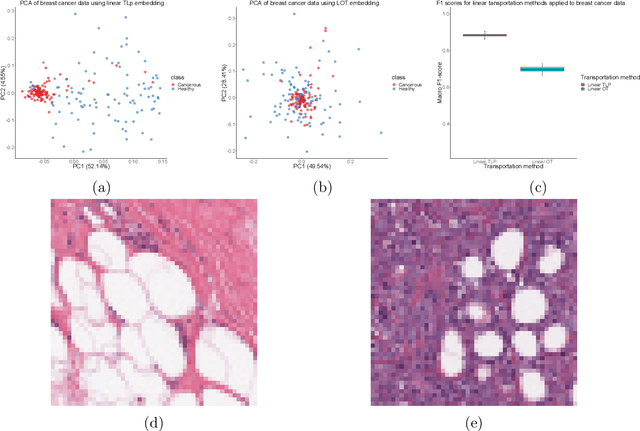
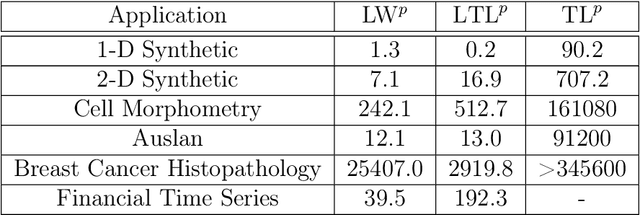
The transportation $\mathrm{L}^p$ distance, denoted $\mathrm{TL}^p$, has been proposed as a generalisation of Wasserstein $\mathrm{W}^p$ distances motivated by the property that it can be applied directly to colour or multi-channelled images, as well as multivariate time-series without normalisation or mass constraints. These distances, as with $\mathrm{W}^p$, are powerful tools in modelling data with spatial or temporal perturbations. However, their computational cost can make them infeasible to apply to even moderate pattern recognition tasks. We propose linear versions of these distances and show that the linear $\mathrm{TL}^p$ distance significantly improves over the linear $\mathrm{W}^p$ distance on signal processing tasks, whilst being several orders of magnitude faster to compute than the $\mathrm{TL}^p$ distance.

Machine learning for COVID-19 detection and prognostication using chest radiographs and CT scans: a systematic methodological review

Background: Machine learning methods offer great potential for fast and accurate detection and prognostication of COVID-19 from standard-of-care chest radiographs (CXR) and computed tomography (CT) images. In this systematic review we critically evaluate the machine learning methodologies employed in the rapidly growing literature. Methods: In this systematic review we reviewed EMBASE via OVID, MEDLINE via PubMed, bioRxiv, medRxiv and arXiv for published papers and preprints uploaded from Jan 1, 2020 to June 24, 2020. Studies which consider machine learning models for the diagnosis or prognosis of COVID-19 from CXR or CT images were included. A methodology quality review of each paper was performed against established benchmarks to ensure the review focusses only on high-quality reproducible papers. This study is registered with PROSPERO [CRD42020188887]. Interpretation: Our review finds that none of the developed models discussed are of potential clinical use due to methodological flaws and underlying biases. This is a major weakness, given the urgency with which validated COVID-19 models are needed. Typically, we find that the documentation of a model's development is not sufficient to make the results reproducible and therefore of 168 candidate papers only 29 are deemed to be reproducible and subsequently considered in this review. We therefore encourage authors to use established machine learning checklists to ensure sufficient documentation is made available, and to follow the PROBAST (prediction model risk of bias assessment tool) framework to determine the underlying biases in their model development process and to mitigate these where possible. This is key to safe clinical implementation which is urgently needed.

Poisson Learning: Graph Based Semi-Supervised Learning At Very Low Label Rates

We propose a new framework, called Poisson learning, for graph based semi-supervised learning at very low label rates. Poisson learning is motivated by the need to address the degeneracy of Laplacian semi-supervised learning in this regime. The method replaces the assignment of label values at training points with the placement of sources and sinks, and solves the resulting Poisson equation on the graph. The outcomes are provably more stable and informative than those of Laplacian learning. Poisson learning is efficient and simple to implement, and we present numerical experiments showing the method is superior to other recent approaches to semi-supervised learning at low label rates on MNIST, FashionMNIST, and Cifar-10. We also propose a graph-cut enhancement of Poisson learning, called Poisson MBO, that gives higher accuracy and can incorporate prior knowledge of relative class sizes.

Rates of Convergence for Laplacian Semi-Supervised Learning with Low Labeling Rates

We study graph-based Laplacian semi-supervised learning at low labeling rates. Laplacian learning uses harmonic extension on a graph to propagate labels. At very low label rates, Laplacian learning becomes degenerate and the solution is roughly constant with spikes at each labeled data point. Previous work has shown that this degeneracy occurs when the number of labeled data points is finite while the number of unlabeled data points tends to infinity. In this work we allow the number of labeled data points to grow to infinity with the number of labels. Our results show that for a random geometric graph with length scale $\varepsilon>0$ and labeling rate $\beta>0$, if $\beta \ll\varepsilon^2$ then the solution becomes degenerate and spikes form, and if $\beta\gg \varepsilon^2$ then Laplacian learning is well-posed and consistent with a continuum Laplace equation. Furthermore, in the well-posed setting we prove quantitative error estimates of $O(\varepsilon\beta^{-1/2})$ for the difference between the solutions of the discrete problem and continuum PDE, up to logarithmic factors. We also study $p$-Laplacian regularization and show the same degeneracy result when $\beta \ll \varepsilon^p$. The proofs of our well-posedness results use the random walk interpretation of Laplacian learning and PDE arguments, while the proofs of the ill-posedness results use $\Gamma$-convergence tools from the calculus of variations. We also present numerical results on synthetic and real data to illustrate our results.