Expected Sliced Transport Plans

The optimal transport (OT) problem has gained significant traction in modern machine learning for its ability to: (1) provide versatile metrics, such as Wasserstein distances and their variants, and (2) determine optimal couplings between probability measures. To reduce the computational complexity of OT solvers, methods like entropic regularization and sliced optimal transport have been proposed. The sliced OT framework improves efficiency by comparing one-dimensional projections (slices) of high-dimensional distributions. However, despite their computational efficiency, sliced-Wasserstein approaches lack a transportation plan between the input measures, limiting their use in scenarios requiring explicit coupling. In this paper, we address two key questions: Can a transportation plan be constructed between two probability measures using the sliced transport framework? If so, can this plan be used to define a metric between the measures? We propose a "lifting" operation to extend one-dimensional optimal transport plans back to the original space of the measures. By computing the expectation of these lifted plans, we derive a new transportation plan, termed expected sliced transport (EST) plans. We prove that using the EST plan to weight the sum of the individual Euclidean costs for moving from one point to another results in a valid metric between the input discrete probability measures. We demonstrate the connection between our approach and the recently proposed min-SWGG, along with illustrative numerical examples that support our theoretical findings.

Signed Cumulative Distribution Transform for Parameter Estimation of 1-D Signals

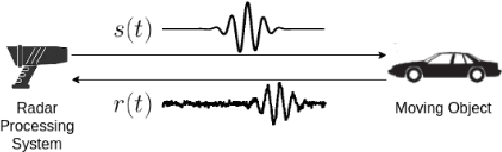
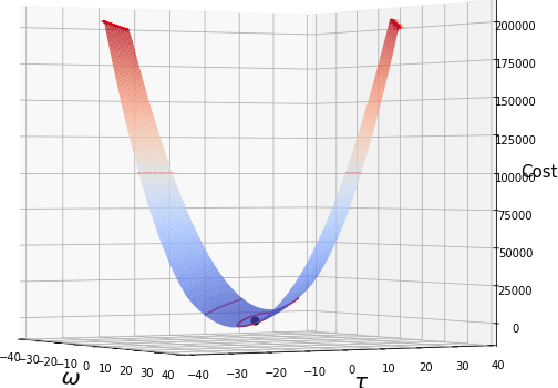
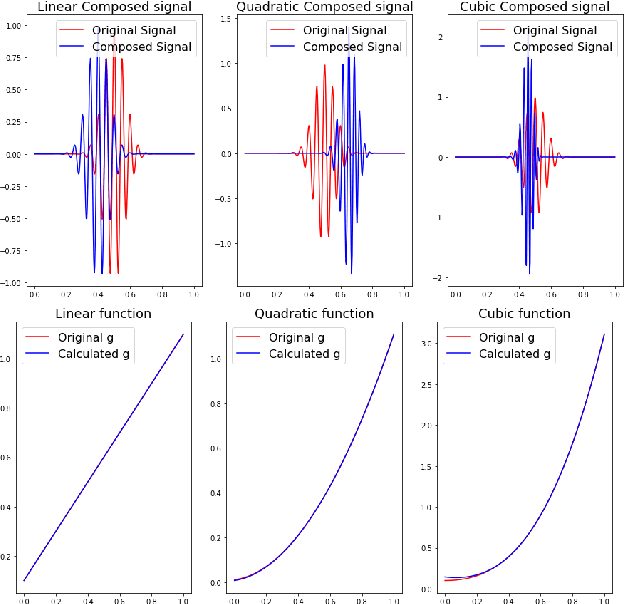
We describe a method for signal parameter estimation using the signed cumulative distribution transform (SCDT), a recently introduced signal representation tool based on optimal transport theory. The method builds upon signal estimation using the cumulative distribution transform (CDT) originally introduced for positive distributions. Specifically, we show that Wasserstein-type distance minimization can be performed simply using linear least squares techniques in SCDT space for arbitrary signal classes, thus providing a global minimizer for the estimation problem even when the underlying signal is a nonlinear function of the unknown parameters. Comparisons to current signal estimation methods using $L_p$ minimization shows the advantage of the method.

The Signed Cumulative Distribution Transform for 1-D Signal Analysis and Classification

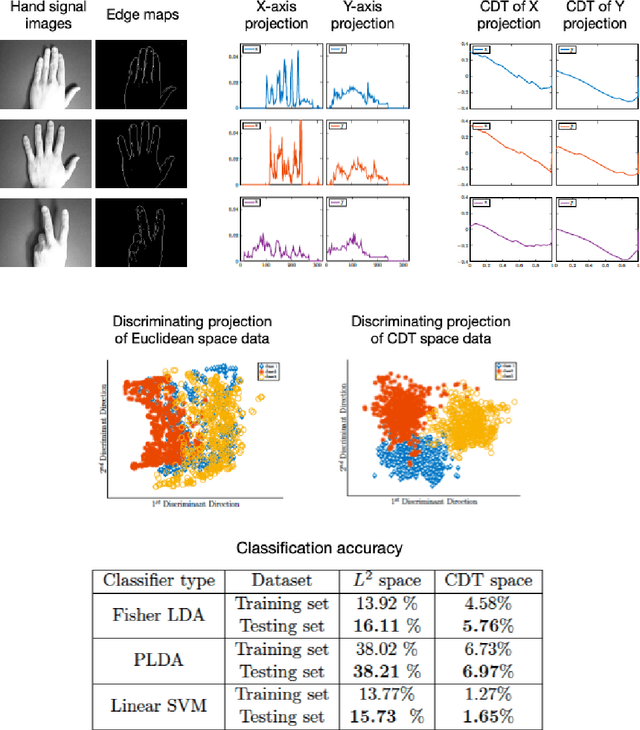
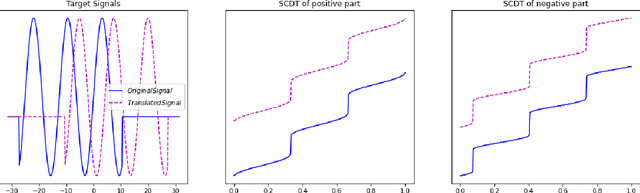
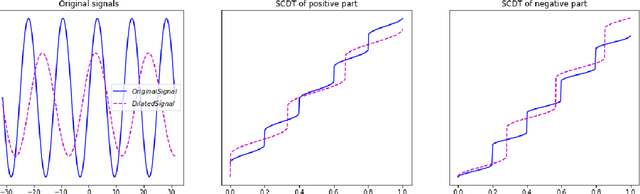
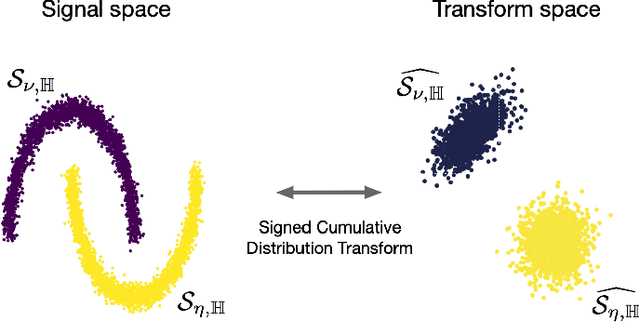
This paper presents a new mathematical signal transform that is especially suitable for decoding information related to non-rigid signal displacements. We provide a measure theoretic framework to extend the existing Cumulative Distribution Transform [ACHA 45 (2018), no. 3, 616-641] to arbitrary (signed) signals on $\overline{\mathbb{R}}$. We present both forward (analysis) and inverse (synthesis) formulas for the transform, and describe several of its properties including translation, scaling, convexity, linear separability and others. Finally, we describe a metric in transform space, and demonstrate the application of the transform in classifying (detecting) signals under random displacements.

Partitioning signal classes using transport transforms for data analysis and machine learning

A relatively new set of transport-based transforms (CDT, R-CDT, LOT) have shown their strength and great potential in various image and data processing tasks such as parametric signal estimation, classification, cancer detection among many others. It is hence worthwhile to elucidate some of the mathematical properties that explain the successes of these transforms when they are used as tools in data analysis, signal processing or data classification. In particular, we give conditions under which classes of signals that are created by algebraic generative models are transformed into convex sets by the transport transforms. Such convexification of the classes simplify the classification and other data analysis and processing problems when viewed in the transform domain. More specifically, we study the extent and limitation of the convexification ability of these transforms under an algebraic generative modeling framework. We hope that this paper will serve as an introduction to these transforms and will encourage mathematicians and other researchers to further explore the theoretical underpinnings and algorithmic tools that will help understand the successes of these transforms and lay the groundwork for further successful applications.

Radon cumulative distribution transform subspace modeling for image classification

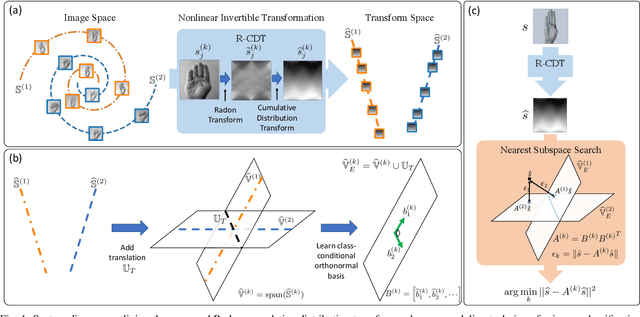
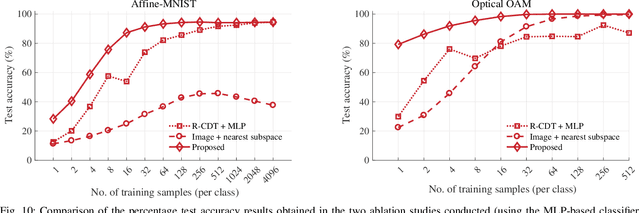
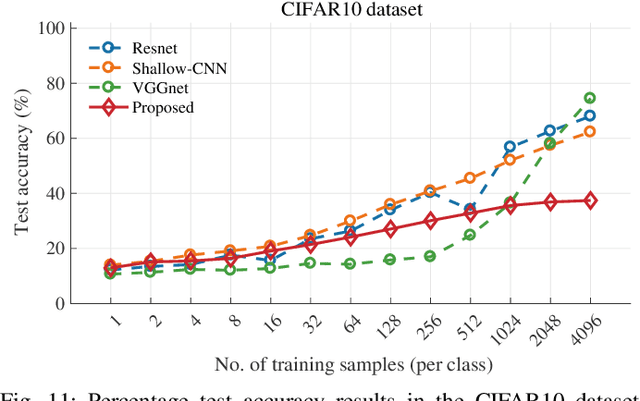
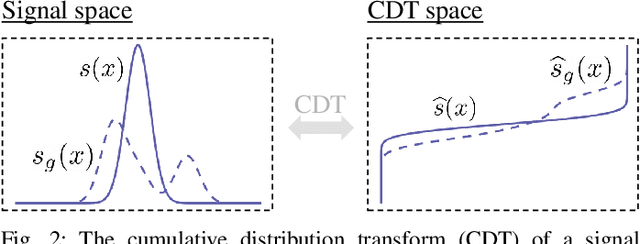
We present a new supervised image classification method for problems where the data at hand conform to certain deformation models applied to unknown prototypes or templates. The method makes use of the previously described Radon Cumulative Distribution Transform (R-CDT) for image data, whose mathematical properties are exploited to express the image data in a form that is more suitable for machine learning. While certain operations such as translation, scaling, and higher-order transformations are challenging to model in native image space, we show the R-CDT can capture some of these variations and thus render the associated image classification problems easier to solve. The method is simple to implement, non-iterative, has no hyper-parameters to tune, it is computationally efficient, and provides competitive accuracies to state-of-the-art neural networks for many types of classification problems, especially in a learning with few labels setting. Furthermore, we show improvements with respect to neural network-based methods in terms of computational efficiency (it can be implemented without the use of GPUs), number of training samples needed for training, as well as out-of-distribution generalization. The Python code for reproducing our results is available at https://github.com/rohdelab/rcdt_ns_classifier.

CUR Decompositions, Similarity Matrices, and Subspace Clustering

A general framework for solving the subspace clustering problem using the CUR decomposition is presented. The CUR decomposition provides a natural way to construct similarity matrices for data that come from a union of unknown subspaces $\mathscr{U}=\underset{i=1}{\overset{M}\bigcup}S_i$. The similarity matrices thus constructed give the exact clustering in the noise-free case. Additionally, this decomposition gives rise to many distinct similarity matrices from a given set of data, which allow enough flexibility to perform accurate clustering of noisy data. We also show that two known methods for subspace clustering can be derived from the CUR decomposition. An algorithm based on the theoretical construction of similarity matrices is presented, and experiments on synthetic and real data are presented to test the method. Additionally, a heuristic algorithm for motion segmentation is presented which yields the best overall performance to date for clustering the Hopkins155 motion dataset.