Training-Free Dual Hyperbolic Adapters for Better Cross-Modal Reasoning

Recent research in Vision-Language Models (VLMs) has significantly advanced our capabilities in cross-modal reasoning. However, existing methods suffer from performance degradation with domain changes or require substantial computational resources for fine-tuning in new domains. To address this issue, we develop a new adaptation method for large vision-language models, called \textit{Training-free Dual Hyperbolic Adapters} (T-DHA). We characterize the vision-language relationship between semantic concepts, which typically has a hierarchical tree structure, in the hyperbolic space instead of the traditional Euclidean space. Hyperbolic spaces exhibit exponential volume growth with radius, unlike the polynomial growth in Euclidean space. We find that this unique property is particularly effective for embedding hierarchical data structures using the Poincaré ball model, achieving significantly improved representation and discrimination power. Coupled with negative learning, it provides more accurate and robust classifications with fewer feature dimensions. Our extensive experimental results on various datasets demonstrate that the T-DHA method significantly outperforms existing state-of-the-art methods in few-shot image recognition and domain generalization tasks.

Laplace Learning in Wasserstein Space

The manifold hypothesis posits that high-dimensional data typically resides on low-dimensional sub spaces. In this paper, we assume manifold hypothesis to investigate graph-based semi-supervised learning methods. In particular, we examine Laplace Learning in the Wasserstein space, extending the classical notion of graph-based semi-supervised learning algorithms from finite-dimensional Euclidean spaces to an infinite-dimensional setting. To achieve this, we prove variational convergence of a discrete graph p- Dirichlet energy to its continuum counterpart. In addition, we characterize the Laplace-Beltrami operator on asubmanifold of the Wasserstein space. Finally, we validate the proposed theoretical framework through numerical experiments conducted on benchmark datasets, demonstrating the consistency of our classification performance in high-dimensional settings.

When is a System Discoverable from Data? Discovery Requires Chaos

The deep learning revolution has spurred a rise in advances of using AI in sciences. Within physical sciences the main focus has been on discovery of dynamical systems from observational data. Yet the reliability of learned surrogates and symbolic models is often undermined by the fundamental problem of non-uniqueness. The resulting models may fit the available data perfectly, but lack genuine predictive power. This raises the question: under what conditions can the systems governing equations be uniquely identified from a finite set of observations? We show, counter-intuitively, that chaos, typically associated with unpredictability, is crucial for ensuring a system is discoverable in the space of continuous or analytic functions. The prevalence of chaotic systems in benchmark datasets may have inadvertently obscured this fundamental limitation. More concretely, we show that systems chaotic on their entire domain are discoverable from a single trajectory within the space of continuous functions, and systems chaotic on a strange attractor are analytically discoverable under a geometric condition on the attractor. As a consequence, we demonstrate for the first time that the classical Lorenz system is analytically discoverable. Moreover, we establish that analytic discoverability is impossible in the presence of first integrals, common in real-world systems. These findings help explain the success of data-driven methods in inherently chaotic domains like weather forecasting, while revealing a significant challenge for engineering applications like digital twins, where stable, predictable behavior is desired. For these non-chaotic systems, we find that while trajectory data alone is insufficient, certain prior physical knowledge can help ensure discoverability. These findings warrant a critical re-evaluation of the fundamental assumptions underpinning purely data-driven discovery.

Learning Regularization Functionals for Inverse Problems: A Comparative Study

In recent years, a variety of learned regularization frameworks for solving inverse problems in imaging have emerged. These offer flexible modeling together with mathematical insights. The proposed methods differ in their architectural design and training strategies, making direct comparison challenging due to non-modular implementations. We address this gap by collecting and unifying the available code into a common framework. This unified view allows us to systematically compare the approaches and highlight their strengths and limitations, providing valuable insights into their future potential. We also provide concise descriptions of each method, complemented by practical guidelines.

LamiGauss: Pitching Radiative Gaussian for Sparse-View X-ray Laminography Reconstruction

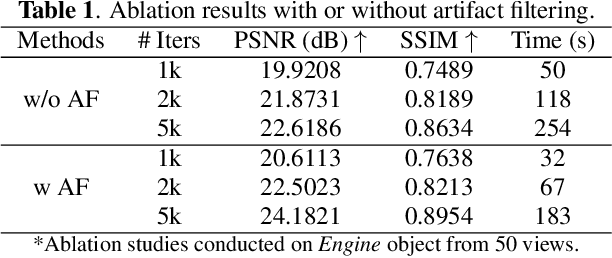
X-ray Computed Laminography (CL) is essential for non-destructive inspection of plate-like structures in applications such as microchips and composite battery materials, where traditional computed tomography (CT) struggles due to geometric constraints. However, reconstructing high-quality volumes from laminographic projections remains challenging, particularly under highly sparse-view acquisition conditions. In this paper, we propose a reconstruction algorithm, namely LamiGauss, that combines Gaussian Splatting radiative rasterization with a dedicated detector-to-world transformation model incorporating the laminographic tilt angle. LamiGauss leverages an initialization strategy that explicitly filters out common laminographic artifacts from the preliminary reconstruction, preventing redundant Gaussians from being allocated to false structures and thereby concentrating model capacity on representing the genuine object. Our approach effectively optimizes directly from sparse projections, enabling accurate and efficient reconstruction with limited data. Extensive experiments on both synthetic and real datasets demonstrate the effectiveness and superiority of the proposed method over existing techniques. LamiGauss uses only 3$\%$ of full views to achieve superior performance over the iterative method optimized on a full dataset.

TANGO: Graph Neural Dynamics via Learned Energy and Tangential Flows

We introduce TANGO -- a dynamical systems inspired framework for graph representation learning that governs node feature evolution through a learned energy landscape and its associated descent dynamics. At the core of our approach is a learnable Lyapunov function over node embeddings, whose gradient defines an energy-reducing direction that guarantees convergence and stability. To enhance flexibility while preserving the benefits of energy-based dynamics, we incorporate a novel tangential component, learned via message passing, that evolves features while maintaining the energy value. This decomposition into orthogonal flows of energy gradient descent and tangential evolution yields a flexible form of graph dynamics, and enables effective signal propagation even in flat or ill-conditioned energy regions, that often appear in graph learning. Our method mitigates oversquashing and is compatible with different graph neural network backbones. Empirically, TANGO achieves strong performance across a diverse set of node and graph classification and regression benchmarks, demonstrating the effectiveness of jointly learned energy functions and tangential flows for graph neural networks.

Data-driven approaches to inverse problems

Inverse problems are concerned with the reconstruction of unknown physical quantities using indirect measurements and are fundamental across diverse fields such as medical imaging, remote sensing, and material sciences. These problems serve as critical tools for visualizing internal structures beyond what is visible to the naked eye, enabling quantification, diagnosis, prediction, and discovery. However, most inverse problems are ill-posed, necessitating robust mathematical treatment to yield meaningful solutions. While classical approaches provide mathematically rigorous and computationally stable solutions, they are constrained by the ability to accurately model solution properties and implement them efficiently. A more recent paradigm considers deriving solutions to inverse problems in a data-driven manner. Instead of relying on classical mathematical modeling, this approach utilizes highly over-parameterized models, typically deep neural networks, which are adapted to specific inverse problems using carefully selected training data. Current approaches that follow this new paradigm distinguish themselves through solution accuracy paired with computational efficiency that was previously inconceivable. These notes offer an introduction to this data-driven paradigm for inverse problems. The first part of these notes will provide an introduction to inverse problems, discuss classical solution strategies, and present some applications. The second part will delve into modern data-driven approaches, with a particular focus on adversarial regularization and provably convergent linear plug-and-play denoisers. Throughout the presentation of these methodologies, their theoretical properties will be discussed, and numerical examples will be provided. The lecture series will conclude with a discussion of open problems and future perspectives in the field.

Return of ChebNet: Understanding and Improving an Overlooked GNN on Long Range Tasks

ChebNet, one of the earliest spectral GNNs, has largely been overshadowed by Message Passing Neural Networks (MPNNs), which gained popularity for their simplicity and effectiveness in capturing local graph structure. Despite their success, MPNNs are limited in their ability to capture long-range dependencies between nodes. This has led researchers to adapt MPNNs through rewiring or make use of Graph Transformers, which compromises the computational efficiency that characterized early spatial message-passing architectures, and typically disregards the graph structure. Almost a decade after its original introduction, we revisit ChebNet to shed light on its ability to model distant node interactions. We find that out-of-box, ChebNet already shows competitive advantages relative to classical MPNNs and GTs on long-range benchmarks, while maintaining good scalability properties for high-order polynomials. However, we uncover that this polynomial expansion leads ChebNet to an unstable regime during training. To address this limitation, we cast ChebNet as a stable and non-dissipative dynamical system, which we coin Stable-ChebNet. Our Stable-ChebNet model allows for stable information propagation, and has controllable dynamics which do not require the use of eigendecompositions, positional encodings, or graph rewiring. Across several benchmarks, Stable-ChebNet achieves near state-of-the-art performance.

Bridging Annotation Gaps: Transferring Labels to Align Object Detection Datasets

Combining multiple object detection datasets offers a path to improved generalisation but is hindered by inconsistencies in class semantics and bounding box annotations. Some methods to address this assume shared label taxonomies and address only spatial inconsistencies; others require manual relabelling, or produce a unified label space, which may be unsuitable when a fixed target label space is required. We propose Label-Aligned Transfer (LAT), a label transfer framework that systematically projects annotations from diverse source datasets into the label space of a target dataset. LAT begins by training dataset-specific detectors to generate pseudo-labels, which are then combined with ground-truth annotations via a Privileged Proposal Generator (PPG) that replaces the region proposal network in two-stage detectors. To further refine region features, a Semantic Feature Fusion (SFF) module injects class-aware context and features from overlapping proposals using a confidence-weighted attention mechanism. This pipeline preserves dataset-specific annotation granularity while enabling many-to-one label space transfer across heterogeneous datasets, resulting in a semantically and spatially aligned representation suitable for training a downstream detector. LAT thus jointly addresses both class-level misalignments and bounding box inconsistencies without relying on shared label spaces or manual annotations. Across multiple benchmarks, LAT demonstrates consistent improvements in target-domain detection performance, achieving gains of up to +4.8AP over semi-supervised baselines.

Smooth Model Compression without Fine-Tuning

Compressing and pruning large machine learning models has become a critical step towards their deployment in real-world applications. Standard pruning and compression techniques are typically designed without taking the structure of the network's weights into account, limiting their effectiveness. We explore the impact of smooth regularization on neural network training and model compression. By applying nuclear norm, first- and second-order derivative penalties of the weights during training, we encourage structured smoothness while preserving predictive performance on par with non-smooth models. We find that standard pruning methods often perform better when applied to these smooth models. Building on this observation, we apply a Singular-Value-Decomposition-based compression method that exploits the underlying smooth structure and approximates the model's weight tensors by smaller low-rank tensors. Our approach enables state-of-the-art compression without any fine-tuning - reaching up to $91\%$ accuracy on a smooth ResNet-18 on CIFAR-10 with $70\%$ fewer parameters.