Channel Shaping Using Beyond Diagonal Reconfigurable Intelligent Surface: Analysis, Optimization, and Enhanced Flexibility

This paper investigates the capability of a passive Reconfigurable Intelligent Surface (RIS) to redistribute the singular values of point-to-point Multiple-Input Multiple-Output (MIMO) channels for achieving power and rate gains. We depart from the conventional Diagonal (D)-RIS with diagonal phase shift matrix and adopt a Beyond Diagonal (BD) architecture that offers greater wave manipulation flexibility through element-wise connections. Specifically, we first provide shaping insights by characterizing the channel singular value regions attainable by D-RIS and BD-RIS via a novel geodesic optimization. Analytical singular value bounds are then derived to explore their shaping limits in typical deployment scenarios. As a side product, we tackle BD-RIS-aided MIMO rate maximization problem by a local-optimal Alternating Optimization (AO) and a shaping-inspired low-complexity approach. Results show that compared to D-RIS, BD-RIS significantly improves the dynamic range of all channel singular values, the trade-off in manipulating them, and thus the channel power and achievable rate. Those observations become more pronounced when the number of RIS elements and MIMO dimensions increase. Of particular interest, BD-RIS is shown to activate multi-stream transmission at lower transmit power than D-RIS, hence achieving the asymptotic Degrees of Freedom (DoF) at low Signal-to-Noise Ratio (SNR) thanks to its higher flexibility of shaping the distribution of channel singular values.

Theoretical Analysis of the Radio Map Estimation Problem

Radio map estimation (RME) constructs representations providing radio frequency metrics, such as the received signal strength, at every location of a geographic area using a set of measurements collected at multiple positions. The resulting radio maps find a wide range of applications in wireless communications, including prediction of coverage holes, network planning, resource allocation, and path planning for mobile robots. Although a vast number of estimators have been proposed, the theoretical understanding of the RME problem has not been pursued. The present work aims at filling this gap along two directions. First, the complexity of the function space of radio maps is quantified by means of lower and upper bounds on their spatial variability, which offers valuable insight into the required spatial distribution of measurements and estimators that can be used. Second, the reconstruction error for power maps in free space is upper bounded for three simple spatial interpolators, namely zeroth-order, first-order, and sinc interpolators. In view of these bounds, the proximity coefficient, which is an increasing function of the transmitted power and a decreasing function of the distance from the transmitters to the mapped region, is proposed to quantify the complexity of the RME problem. Simple numerical experiments assess the tightness of the obtained bounds and reveal the practical trade-offs associated with the considered interpolators.

Understanding the Limits of Poisoning Attacks in Episodic Reinforcement Learning

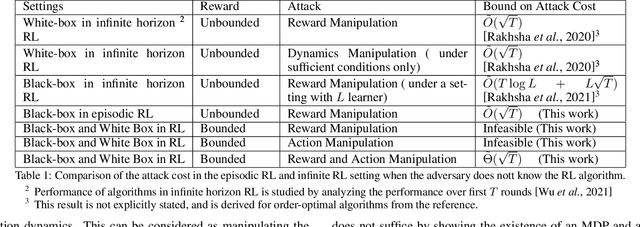
To understand the security threats to reinforcement learning (RL) algorithms, this paper studies poisoning attacks to manipulate \emph{any} order-optimal learning algorithm towards a targeted policy in episodic RL and examines the potential damage of two natural types of poisoning attacks, i.e., the manipulation of \emph{reward} and \emph{action}. We discover that the effect of attacks crucially depend on whether the rewards are bounded or unbounded. In bounded reward settings, we show that only reward manipulation or only action manipulation cannot guarantee a successful attack. However, by combining reward and action manipulation, the adversary can manipulate any order-optimal learning algorithm to follow any targeted policy with $\tilde{\Theta}(\sqrt{T})$ total attack cost, which is order-optimal, without any knowledge of the underlying MDP. In contrast, in unbounded reward settings, we show that reward manipulation attacks are sufficient for an adversary to successfully manipulate any order-optimal learning algorithm to follow any targeted policy using $\tilde{O}(\sqrt{T})$ amount of contamination. Our results reveal useful insights about what can or cannot be achieved by poisoning attacks, and are set to spur more works on the design of robust RL algorithms.

Secure-UCB: Saving Stochastic Bandits from Poisoning Attacks via Limited Data Verification

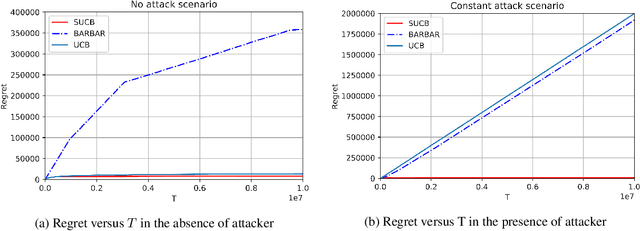
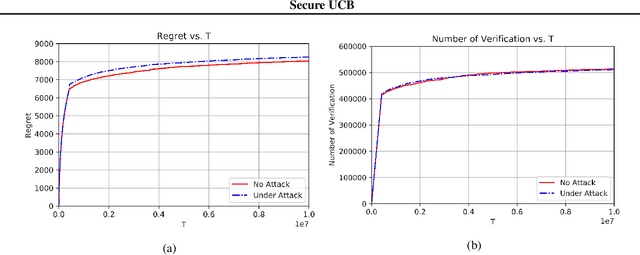
This paper studies bandit algorithms under data poisoning attacks in a bounded reward setting. We consider a strong attacker model in which the attacker can observe both the selected actions and their corresponding rewards, and can contaminate the rewards with additive noise. We show that \emph{any} bandit algorithm with regret $O(\log T)$ can be forced to suffer a regret $\Omega(T)$ with an expected amount of contamination $O(\log T)$. This amount of contamination is also necessary, as we prove that there exists an $O(\log T)$ regret bandit algorithm, specifically the classical UCB, that requires $\Omega(\log T)$ amount of contamination to suffer regret $\Omega(T)$. To combat such poising attacks, our second main contribution is to propose a novel algorithm, Secure-UCB, which uses limited \emph{verification} to access a limited number of uncontaminated rewards. We show that with $O(\log T)$ expected number of verifications, Secure-UCB can restore the order optimal $O(\log T)$ regret \emph{irrespective of the amount of contamination} used by the attacker. Finally, we prove that for any bandit algorithm, this number of verifications $O(\log T)$ is necessary to recover the order-optimal regret. We can then conclude that Secure-UCB is order-optimal in terms of both the expected regret and the expected number of verifications, and can save stochastic bandits from any data poisoning attack.

Sequential Choice Bandits with Feedback for Personalizing users' experience

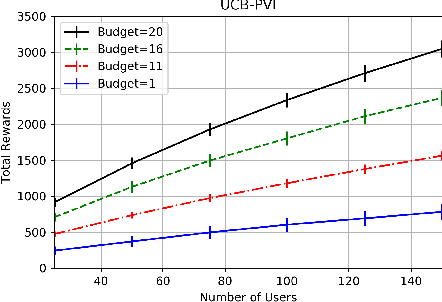
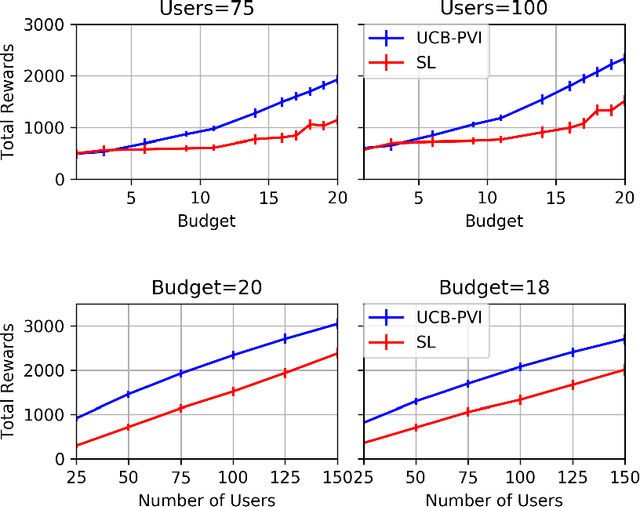
In this work, we study sequential choice bandits with feedback. We propose bandit algorithms for a platform that personalizes users' experience to maximize its rewards. For each action directed to a given user, the platform is given a positive reward, which is a non-decreasing function of the action, if this action is below the user's threshold. Users are equipped with a patience budget, and actions that are above the threshold decrease the user's patience. When all patience is lost, the user abandons the platform. The platform attempts to learn the thresholds of the users in order to maximize its rewards, based on two different feedback models describing the information pattern available to the platform at each action. We define a notion of regret by determining the best action to be taken when the platform knows that the user's threshold is in a given interval. We then propose bandit algorithms for the two feedback models and show that upper and lower bounds on the regret are of the order of $\tilde{O}(N^{2/3})$ and $\tilde\Omega(N^{2/3})$, respectively, where $N$ is the total number of users. Finally, we show that the waiting time of any user before receiving a personalized experience is uniform in $N$.

Control Barriers in Bayesian Learning of System Dynamics

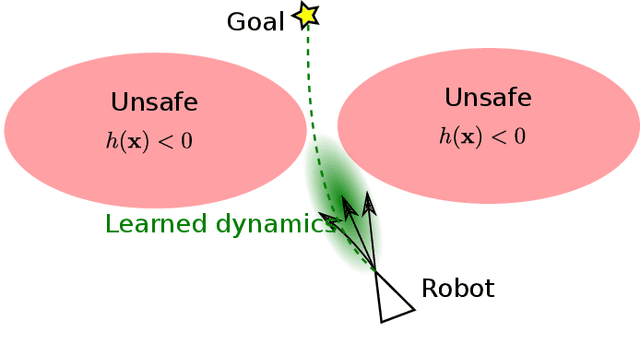
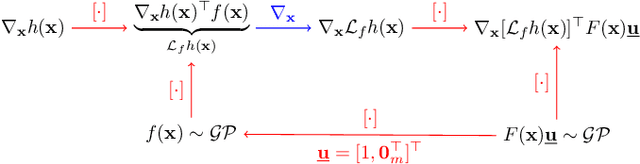
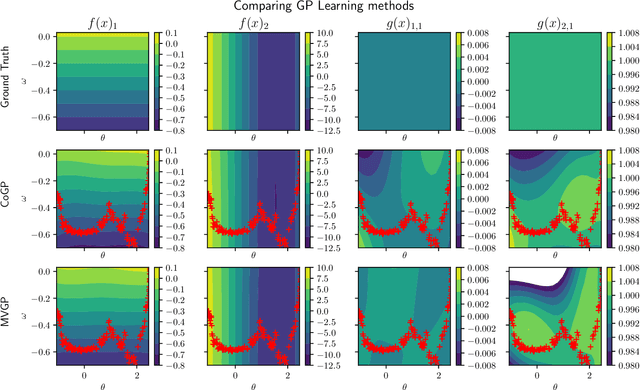
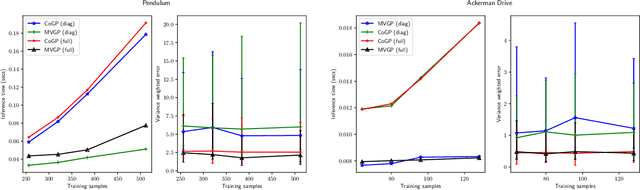
This paper focuses on learning a model of system dynamics online while satisfying safety constraints. Our objective is to avoid offline system identification or hand-specified models and allow a system to safely and autonomously estimate and adapt its own model during operation. Given streaming observations of the system state, we use Bayesian learning to obtain a distribution over the system dynamics. Specifically, we use a matrix variate Gaussian process (MVGP) regression approach with efficient covariance factorization to learn the drift and input gain terms of a nonlinear control-affine system. The MVGP distribution is then used to optimize the system behavior and ensure safety with high probability, by specifying control Lyapunov function (CLF) and control barrier function (CBF) chance constraints. We show that a safe control policy can be synthesized for systems with arbitrary relative degree and probabilistic CLF-CBF constraints by solving a second order cone program (SOCP). Finally, we extend our design to a self-triggering formulation, adaptively determining the time at which a new control input needs to be applied in order to guarantee safety.

Learning-based attacks in Cyber-Physical Systems: Exploration, Detection, and Control Cost trade-offs

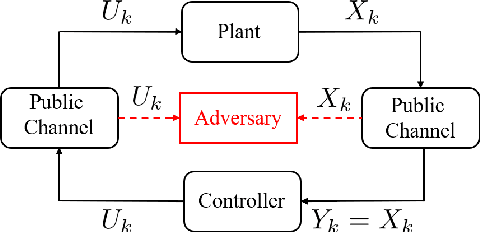
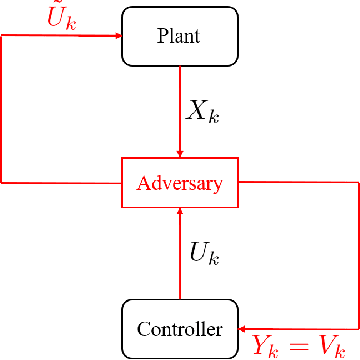
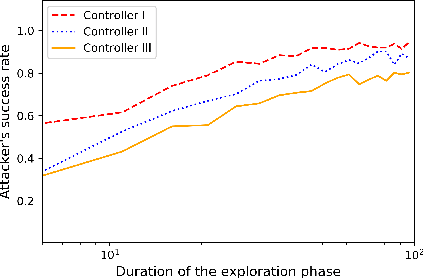
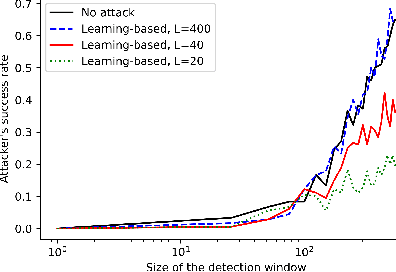
We study the problem of learning-based attacks in linear systems, where the communication channel between the controller and the plant can be hijacked by a malicious attacker. We assume the attacker learns the dynamics of the system from observations, then overrides the controller's actuation signal, while mimicking legitimate operation by providing fictitious sensor readings to the controller. On the other hand, the controller is on a lookout to detect the presence of the attacker and tries to enhance the detection performance by carefully crafting its control signals. We study the trade-offs between the information acquired by the attacker from observations, the detection capabilities of the controller, and the control cost. Specifically, we provide tight upper and lower bounds on the expected $\epsilon$-deception time, namely the time required by the controller to make a decision regarding the presence of an attacker with confidence at least $(1-\epsilon\log(1/\epsilon))$. We then show a probabilistic lower bound on the time that must be spent by the attacker learning the system, in order for the controller to have a given expected $\epsilon$-deception time. We show that this bound is also order optimal, in the sense that if the attacker satisfies it, then there exists a learning algorithm with the given order expected deception time. Finally, we show a lower bound on the expected energy expenditure required to guarantee detection with confidence at least $1-\epsilon \log(1/\epsilon)$.

Probabilistic Safety Constraints for Learned High Relative Degree System Dynamics

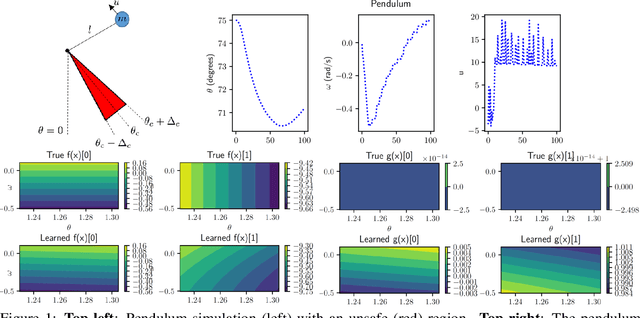
This paper focuses on learning a model of system dynamics online while satisfying safety constraints. Our motivation is to avoid offline system identification or hand-specified dynamics models and allow a system to safely and autonomously estimate and adapt its own model during online operation. Given streaming observations of the system state, we use Bayesian learning to obtain a distribution over the system dynamics. In turn, the distribution is used to optimize the system behavior and ensure safety with high probability, by specifying a chance constraint over a control barrier function.

Associative Convolutional Layers

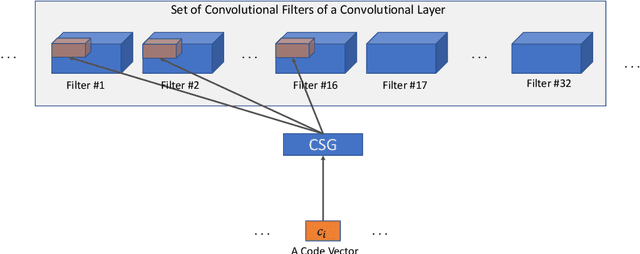
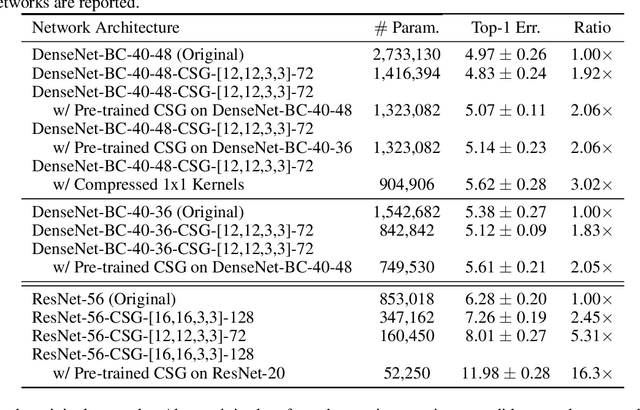
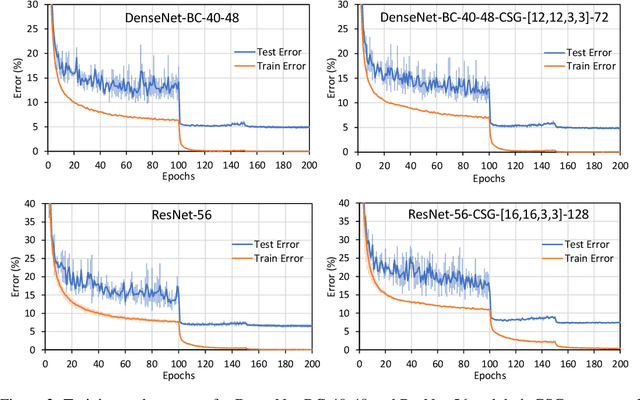
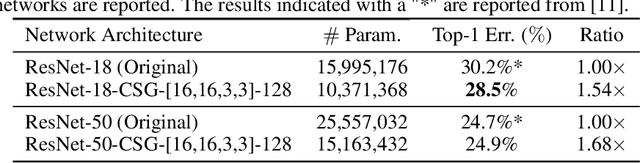
Motivated by the necessity for parameter efficiency in distributed machine learning and AI-enabled edge devices, we provide a general and easy to implement method for significantly reducing the number of parameters of Convolutional Neural Networks (CNNs), during both the training and inference phases. We introduce a simple auxiliary neural network which can generate the convolutional filters of any CNN architecture from a low dimensional latent space. This auxiliary neural network, which we call "Convolutional Slice Generator" (CSG), is unique to the network and provides the association between its convolutional layers. During the training of the CNN, instead of training the filters of the convolutional layers, only the parameters of the CSG and their corresponding `code vectors' are trained. This results in a significant reduction of the number of parameters due to the fact that the CNN can be fully represented using only the parameters of the CSG, the code vectors, the fully connected layers, and the architecture of the CNN. To show the capability of our method, we apply it to ResNet and DenseNet architectures, using the CIFAR-10 dataset without any hyper-parameter tuning. Experiments show that our approach, even when applied to already compressed and efficient CNNs such as DenseNet-BC, significantly reduces the number of network parameters. In two models based on DenseNet-BC with $\approx 2\times$ reduction in one of them we had a slight improvement in accuracy and in another one, with $\approx 2\times$ reduction the change in accuracy is negligible. In case of ResNet-56, $\approx 2.5\times$ reduction leads to an accuracy loss within $1\%$.

Online learning with feedback graphs and switching costs

We study online learning when partial feedback information is provided following every action of the learning process, and the learner incurs switching costs for changing his actions. In this setting, the feedback information system can be represented by a graph, and previous work provided the expected regret of the learner in the case of a clique (Expert setup), or disconnected single loops (Multi-Armed Bandits). We provide a lower bound on the expected regret in the partial information (PI) setting, namely for general feedback graphs ---excluding the clique. We show that all algorithms that are optimal without switching costs are necessarily sub-optimal in the presence of switching costs, which motivates the need to design new algorithms in this setup. We propose two novel algorithms: Threshold Based EXP3 and EXP3.SC. For the two special cases of symmetric PI setting and Multi-Armed-Bandits, we show that the expected regret of both algorithms is order optimal in the duration of the learning process with a pre-constant dependent on the feedback system. Additionally, we show that Threshold Based EXP3 is order optimal in the switching cost, whereas EXP3.SC is not. Finally, empirical evaluations show that Threshold Based EXP3 outperforms previous algorithm EXP3 SET in the presence of switching costs, and Batch EXP3 in the special setting of Multi-Armed Bandits with switching costs, where both algorithms are order optimal.