RoMo: Robust Motion Segmentation Improves Structure from Motion

There has been extensive progress in the reconstruction and generation of 4D scenes from monocular casually-captured video. While these tasks rely heavily on known camera poses, the problem of finding such poses using structure-from-motion (SfM) often depends on robustly separating static from dynamic parts of a video. The lack of a robust solution to this problem limits the performance of SfM camera-calibration pipelines. We propose a novel approach to video-based motion segmentation to identify the components of a scene that are moving w.r.t. a fixed world frame. Our simple but effective iterative method, RoMo, combines optical flow and epipolar cues with a pre-trained video segmentation model. It outperforms unsupervised baselines for motion segmentation as well as supervised baselines trained from synthetic data. More importantly, the combination of an off-the-shelf SfM pipeline with our segmentation masks establishes a new state-of-the-art on camera calibration for scenes with dynamic content, outperforming existing methods by a substantial margin.

Efficient CDF Approximations for Normalizing Flows

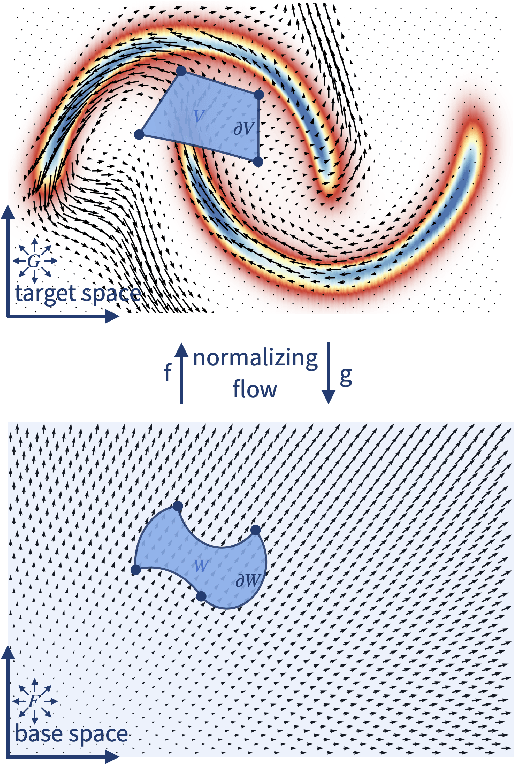
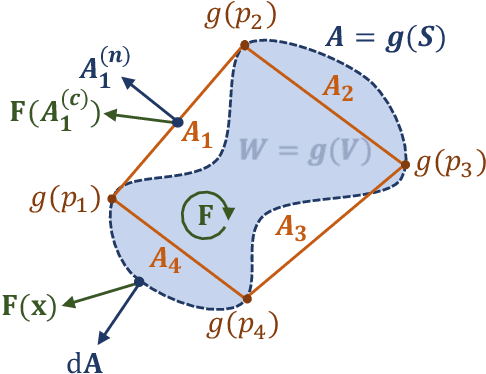
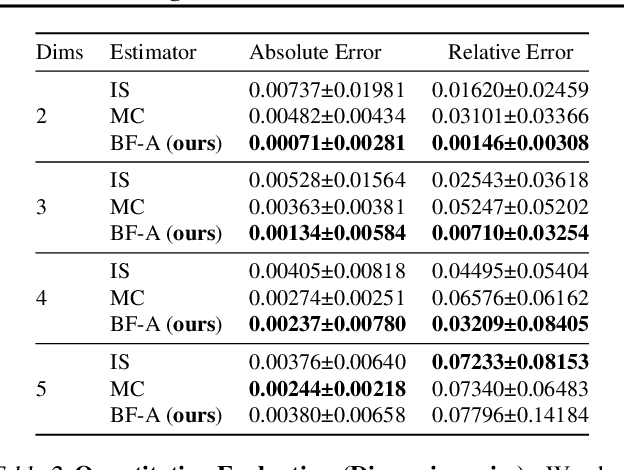
Normalizing flows model a complex target distribution in terms of a bijective transform operating on a simple base distribution. As such, they enable tractable computation of a number of important statistical quantities, particularly likelihoods and samples. Despite these appealing properties, the computation of more complex inference tasks, such as the cumulative distribution function (CDF) over a complex region (e.g., a polytope) remains challenging. Traditional CDF approximations using Monte-Carlo techniques are unbiased but have unbounded variance and low sample efficiency. Instead, we build upon the diffeomorphic properties of normalizing flows and leverage the divergence theorem to estimate the CDF over a closed region in target space in terms of the flux across its \emph{boundary}, as induced by the normalizing flow. We describe both deterministic and stochastic instances of this estimator: while the deterministic variant iteratively improves the estimate by strategically subdividing the boundary, the stochastic variant provides unbiased estimates. Our experiments on popular flow architectures and UCI benchmark datasets show a marked improvement in sample efficiency as compared to traditional estimators.

Point Process Flows

Event sequences can be modeled by temporal point processes (TPPs) to capture their asynchronous and probabilistic nature. We propose an intensity-free framework that directly models the point process distribution by utilizing normalizing flows. This approach is capable of capturing highly complex temporal distributions and does not rely on restrictive parametric forms. Comparisons with state-of-the-art baseline models on both synthetic and challenging real-life datasets show that the proposed framework is effective at modeling the stochasticity of discrete event sequences.

Parity Partition Coding for Sharp Multi-Label Classification

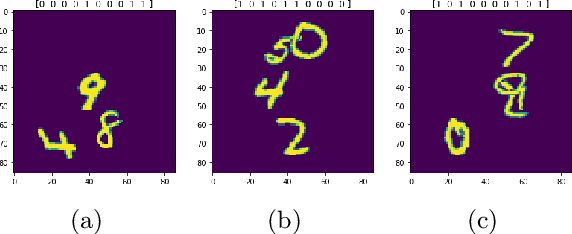
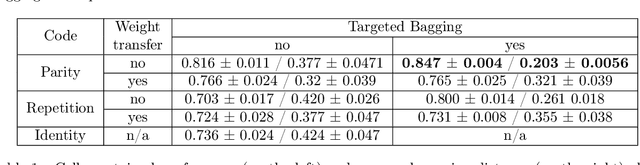
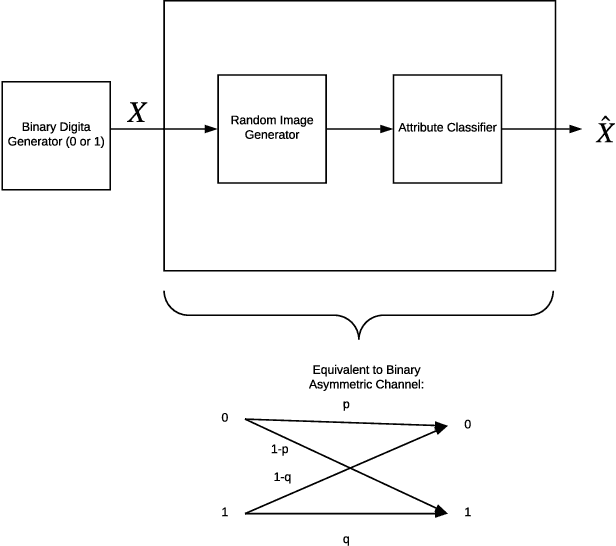
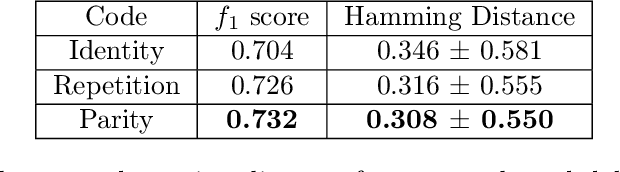
The problem of efficiently training and evaluating image classifiers that can distinguish between a large number of object categories is considered. A novel metric, sharpness, is proposed which is defined as the fraction of object categories that are above a threshold accuracy. To estimate sharpness (along with a confidence value), a technique called fraction-accurate estimation is introduced which samples categories and samples instances from these categories. In addition, a technique called parity partition coding, a special type of error correcting output code, is introduced, increasing sharpness, while reducing the multi-class problem to a multi-label one with exponentially fewer outputs. We demonstrate that this approach outperforms the baseline model for both MultiMNIST and CelebA, while requiring fewer parameters and exceeding state of the art accuracy on individual labels.

Time2Vec: Learning a Vector Representation of Time

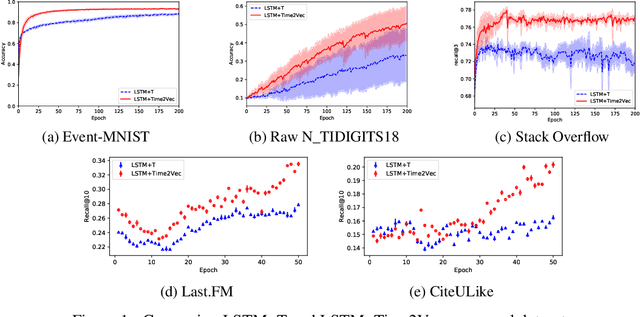
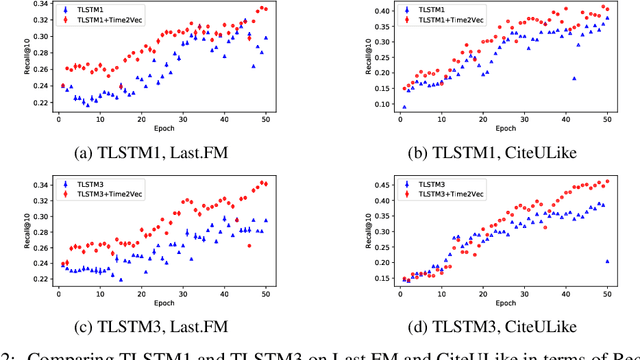
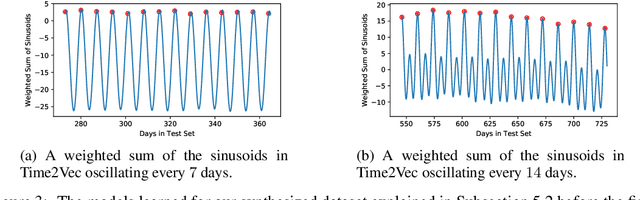
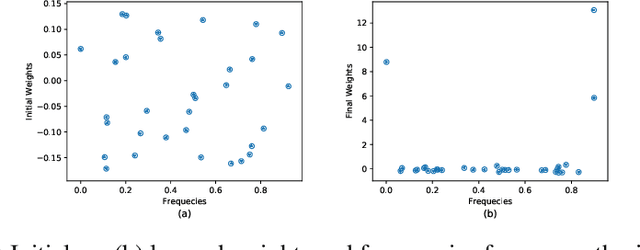
Time is an important feature in many applications involving events that occur synchronously and/or asynchronously. To effectively consume time information, recent studies have focused on designing new architectures. In this paper, we take an orthogonal but complementary approach by providing a model-agnostic vector representation for time, called Time2Vec, that can be easily imported into many existing and future architectures and improve their performances. We show on a range of models and problems that replacing the notion of time with its Time2Vec representation improves the performance of the final model.

Tails of Triangular Flows

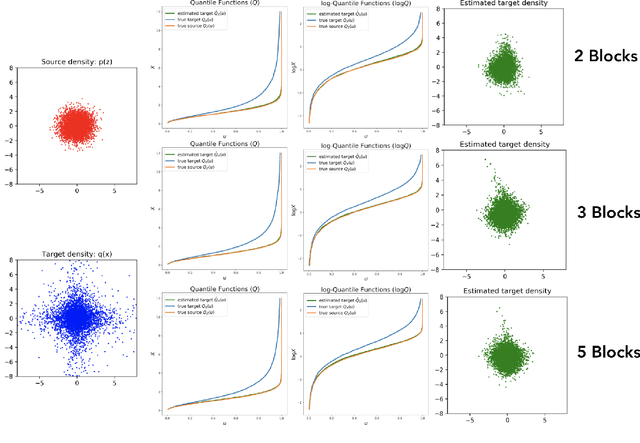
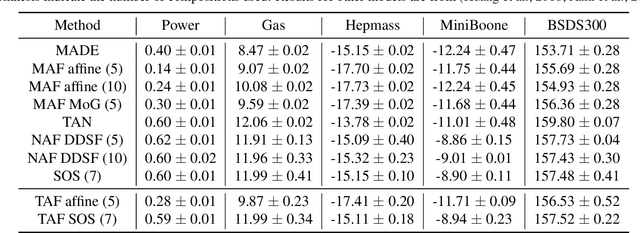
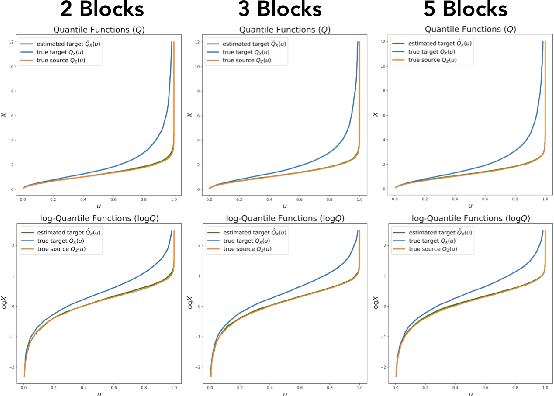
Triangular maps are a construct in probability theory that allows the transformation of any source density to any target density. We consider flow based models that learn these triangular transformations which we call triangular flows and study the properties of these triangular flows with the goal of capturing heavy tailed target distributions.In one dimension, we prove that the density quantile functions of the source and target density can characterize properties of the increasing push-forward transformation and show that no Lipschitz continuous increasing map can transform a light-tailed source to a heavy-tailed target density. We further precisely relate the asymptotic behavior of these density quantile functions with the existence of certain function moments of distributions. These results allow us to give a precise asymptotic rate at which an increasing transformation must grow to capture the tail properties of a target given the source distribution. In the multivariate case, we show that any increasing triangular map transforming a light-tailed source density to a heavy-tailed target density must have all eigenvalues of the Jacobian to be unbounded. Our analysis suggests the importance of source distribution in capturing heavy-tailed distributions and we discuss the implications for flow based models.

Diachronic Embedding for Temporal Knowledge Graph Completion

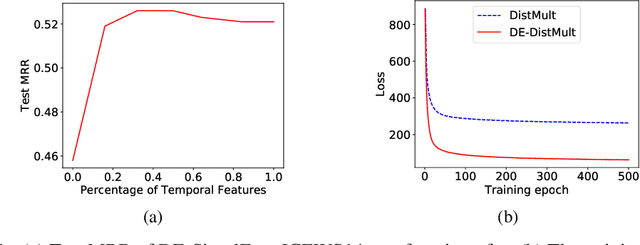
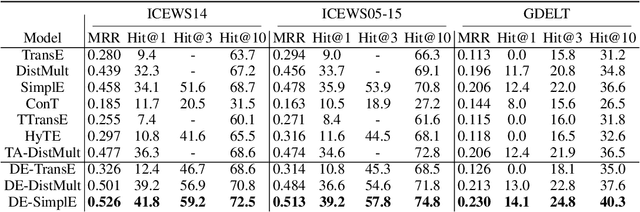
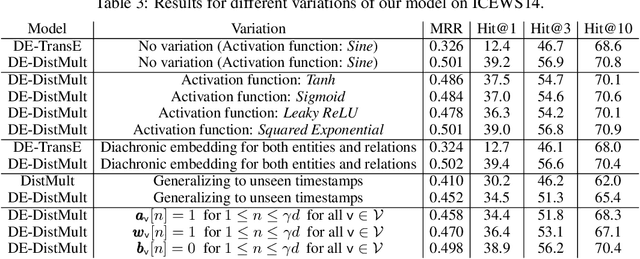
Knowledge graphs (KGs) typically contain temporal facts indicating relationships among entities at different times. Due to their incompleteness, several approaches have been proposed to infer new facts for a KG based on the existing ones-a problem known as KG completion. KG embedding approaches have proved effective for KG completion, however, they have been developed mostly for static KGs. Developing temporal KG embedding models is an increasingly important problem. In this paper, we build novel models for temporal KG completion through equipping static models with a diachronic entity embedding function which provides the characteristics of entities at any point in time. This is in contrast to the existing temporal KG embedding approaches where only static entity features are provided. The proposed embedding function is model-agnostic and can be potentially combined with any static model. We prove that combining it with SimplE, a recent model for static KG embedding, results in a fully expressive model for temporal KG completion. Our experiments indicate the superiority of our proposal compared to existing baselines.

Differentiable probabilistic models of scientific imaging with the Fourier slice theorem

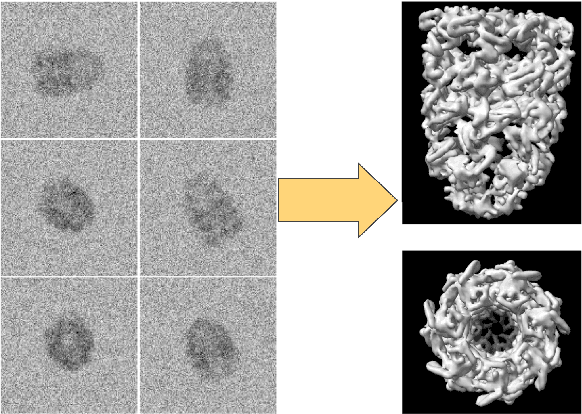
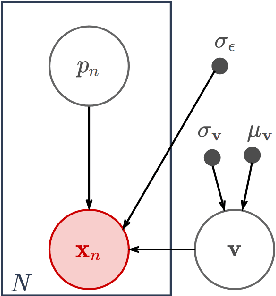
Scientific imaging techniques such as optical and electron microscopy and computed tomography (CT) scanning are used to study the 3D structure of an object through 2D observations. These observations are related to the original 3D object through orthogonal integral projections. For common 3D reconstruction algorithms, computational efficiency requires the modeling of the 3D structures to take place in Fourier space by applying the Fourier slice theorem. At present, it is unclear how to differentiate through the projection operator, and hence current learning algorithms can not rely on gradient based methods to optimize 3D structure models. In this paper we show how back-propagation through the projection operator in Fourier space can be achieved. We demonstrate the validity of the approach with experiments on 3D reconstruction of proteins. We further extend our approach to learning probabilistic models of 3D objects. This allows us to predict regions of low sampling rates or estimate noise. A higher sample efficiency can be reached by utilizing the learned uncertainties of the 3D structure as an unsupervised estimate of the model fit. Finally, we demonstrate how the reconstruction algorithm can be extended with an amortized inference scheme on unknown attributes such as object pose. Through empirical studies we show that joint inference of the 3D structure and the object pose becomes more difficult when the ground truth object contains more symmetries. Due to the presence of for instance (approximate) rotational symmetries, the pose estimation can easily get stuck in local optima, inhibiting a fine-grained high-quality estimate of the 3D structure.

On the Effectiveness of Low Frequency Perturbations

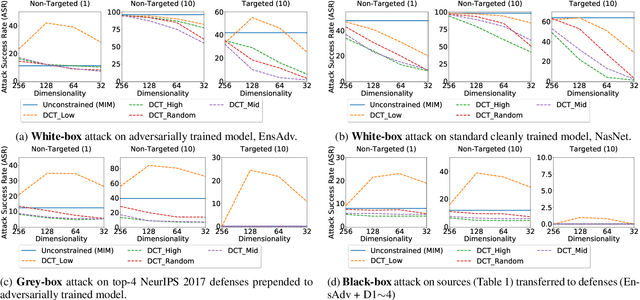
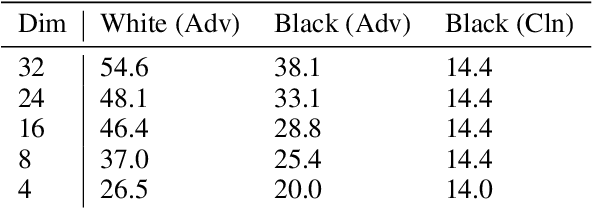
Carefully crafted, often imperceptible, adversarial perturbations have been shown to cause state-of-the-art models to yield extremely inaccurate outputs, rendering them unsuitable for safety-critical application domains. In addition, recent work has shown that constraining the attack space to a low frequency regime is particularly effective. Yet, it remains unclear whether this is due to generally constraining the attack search space or specifically removing high frequency components from consideration. By systematically controlling the frequency components of the perturbation, evaluating against the top-placing defense submissions in the NeurIPS 2017 competition, we empirically show that performance improvements in both optimization and generalization are yielded only when low frequency components are preserved. In fact, the defended models based on (ensemble) adversarial training are roughly as vulnerable to low frequency perturbations as undefended models, suggesting that the purported robustness of proposed defenses is reliant upon adversarial perturbations being high frequency in nature. We do find that under $\ell_\infty$ $\epsilon=16/255$, a commonly used distortion bound, low frequency perturbations are indeed perceptible. This questions the use of the $\ell_\infty$-norm, in particular, as a distortion metric, and suggests that explicitly considering the frequency space is promising for learning robust models which better align with human perception.