What makes an image realistic?

The last decade has seen tremendous progress in our ability to generate realistic-looking data, be it images, text, audio, or video. Here, we discuss the closely related problem of quantifying realism, that is, designing functions that can reliably tell realistic data from unrealistic data. This problem turns out to be significantly harder to solve and remains poorly understood, despite its prevalence in machine learning and recent breakthroughs in generative AI. Drawing on insights from algorithmic information theory, we discuss why this problem is challenging, why a good generative model alone is insufficient to solve it, and what a good solution would look like. In particular, we introduce the notion of a universal critic, which unlike adversarial critics does not require adversarial training. While universal critics are not immediately practical, they can serve both as a North Star for guiding practical implementations and as a tool for analyzing existing attempts to capture realism.

C3: High-performance and low-complexity neural compression from a single image or video

Most neural compression models are trained on large datasets of images or videos in order to generalize to unseen data. Such generalization typically requires large and expressive architectures with a high decoding complexity. Here we introduce C3, a neural compression method with strong rate-distortion (RD) performance that instead overfits a small model to each image or video separately. The resulting decoding complexity of C3 can be an order of magnitude lower than neural baselines with similar RD performance. C3 builds on COOL-CHIC (Ladune et al.) and makes several simple and effective improvements for images. We further develop new methodology to apply C3 to videos. On the CLIC2020 image benchmark, we match the RD performance of VTM, the reference implementation of the H.266 codec, with less than 3k MACs/pixel for decoding. On the UVG video benchmark, we match the RD performance of the Video Compression Transformer (Mentzer et al.), a well-established neural video codec, with less than 5k MACs/pixel for decoding.

The Unreasonable Effectiveness of Linear Prediction as a Perceptual Metric

We show how perceptual embeddings of the visual system can be constructed at inference-time with no training data or deep neural network features. Our perceptual embeddings are solutions to a weighted least squares (WLS) problem, defined at the pixel-level, and solved at inference-time, that can capture global and local image characteristics. The distance in embedding space is used to define a perceptual similarity metric which we call LASI: Linear Autoregressive Similarity Index. Experiments on full-reference image quality assessment datasets show LASI performs competitively with learned deep feature based methods like LPIPS (Zhang et al., 2018) and PIM (Bhardwaj et al., 2020), at a similar computational cost to hand-crafted methods such as MS-SSIM (Wang et al., 2003). We found that increasing the dimensionality of the embedding space consistently reduces the WLS loss while increasing performance on perceptual tasks, at the cost of increasing the computational complexity. LASI is fully differentiable, scales cubically with the number of embedding dimensions, and can be parallelized at the pixel-level. A Maximum Differentiation (MAD) competition (Wang & Simoncelli, 2008) between LASI and LPIPS shows that both methods are capable of finding failure points for the other, suggesting these metrics can be combined.

Wasserstein Distortion: Unifying Fidelity and Realism

We introduce a distortion measure for images, Wasserstein distortion, that simultaneously generalizes pixel-level fidelity on the one hand and realism on the other. We show how Wasserstein distortion reduces mathematically to a pure fidelity constraint or a pure realism constraint under different parameter choices. Pairs of images that are close under Wasserstein distortion illustrate its utility. In particular, we generate random textures that have high fidelity to a reference texture in one location of the image and smoothly transition to an independent realization of the texture as one moves away from this point. Connections between Wasserstein distortion and models of the human visual system are noted.

High-Fidelity Image Compression with Score-based Generative Models

Despite the tremendous success of diffusion generative models in text-to-image generation, replicating this success in the domain of image compression has proven difficult. In this paper, we demonstrate that diffusion can significantly improve perceptual quality at a given bit-rate, outperforming state-of-the-art approaches PO-ELIC and HiFiC as measured by FID score. This is achieved using a simple but theoretically motivated two-stage approach combining an autoencoder targeting MSE followed by a further score-based decoder. However, as we will show, implementation details matter and the optimal design decisions can differ greatly from typical text-to-image models.

Lossy Compression with Gaussian Diffusion

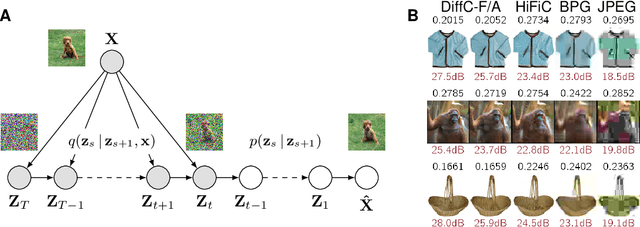
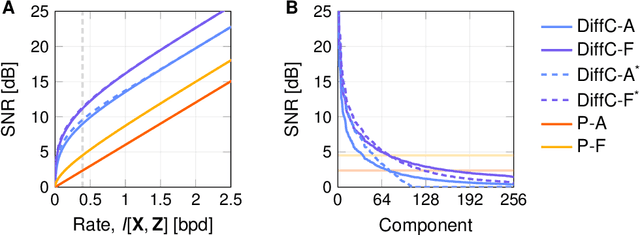
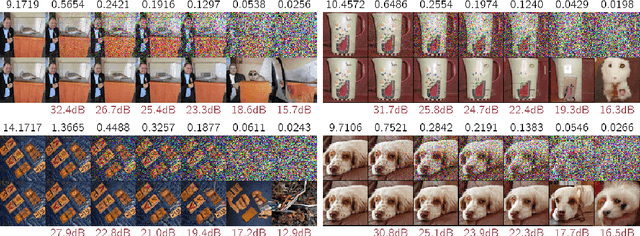
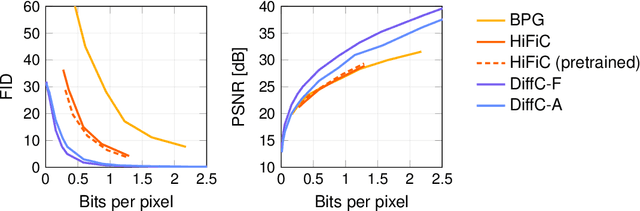
We describe a novel lossy compression approach called DiffC which is based on unconditional diffusion generative models. Unlike modern compression schemes which rely on transform coding and quantization to restrict the transmitted information, DiffC relies on the efficient communication of pixels corrupted by Gaussian noise. We implement a proof of concept and find that it works surprisingly well despite the lack of an encoder transform, outperforming the state-of-the-art generative compression method HiFiC on ImageNet 64x64. DiffC only uses a single model to encode and denoise corrupted pixels at arbitrary bitrates. The approach further provides support for progressive coding, that is, decoding from partial bit streams. We perform a rate-distortion analysis to gain a deeper understanding of its performance, providing analytical results for multivariate Gaussian data as well as initial results for general distributions. Furthermore, we show that a flow-based reconstruction achieves a 3 dB gain over ancestral sampling at high bitrates.

An Introduction to Neural Data Compression

Neural compression is the application of neural networks and other machine learning methods to data compression. While machine learning deals with many concepts closely related to compression, entering the field of neural compression can be difficult due to its reliance on information theory, perceptual metrics, and other knowledge specific to the field. This introduction hopes to fill in the necessary background by reviewing basic coding topics such as entropy coding and rate-distortion theory, related machine learning ideas such as bits-back coding and perceptual metrics, and providing a guide through the representative works in the literature so far.

Optimal Compression of Locally Differentially Private Mechanisms

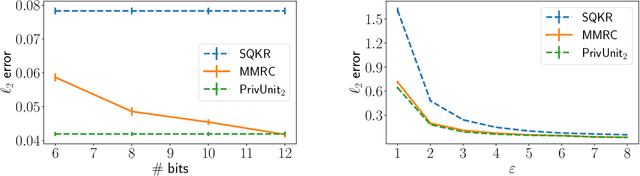
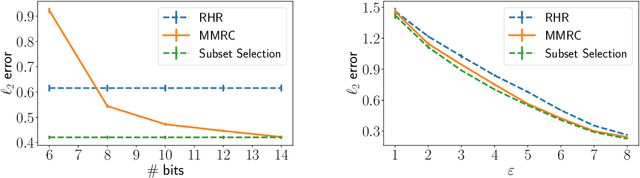
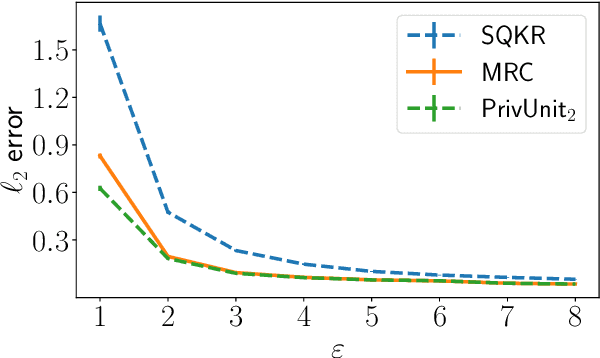
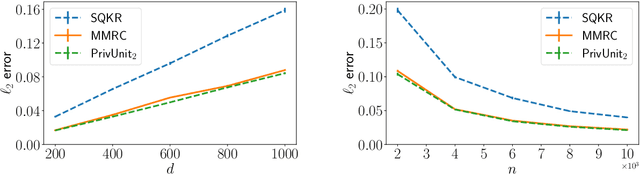
Compressing the output of \epsilon-locally differentially private (LDP) randomizers naively leads to suboptimal utility. In this work, we demonstrate the benefits of using schemes that jointly compress and privatize the data using shared randomness. In particular, we investigate a family of schemes based on Minimal Random Coding (Havasi et al., 2019) and prove that they offer optimal privacy-accuracy-communication tradeoffs. Our theoretical and empirical findings show that our approach can compress PrivUnit (Bhowmick et al., 2018) and Subset Selection (Ye et al., 2018), the best known LDP algorithms for mean and frequency estimation, to to the order of \epsilon-bits of communication while preserving their privacy and accuracy guarantees.

Algorithms for the Communication of Samples

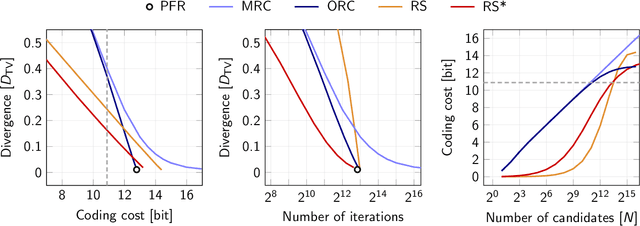
We consider the problem of reverse channel coding, that is, how to simulate a noisy channel over a digital channel efficiently. We propose two new coding schemes with practical advantages over previous approaches. First, we introduce ordered random coding (ORC) which uses a simple trick to reduce the coding cost of previous approaches based on importance sampling. Our derivation also illuminates a connection between these schemes and the so-called Poisson functional representation. Second, we describe a hybrid coding scheme which uses dithered quantization to efficiently communicate samples from distributions with bounded support.

A coding theorem for the rate-distortion-perception function

The rate-distortion-perception function (RDPF; Blau and Michaeli, 2019) has emerged as a useful tool for thinking about realism and distortion of reconstructions in lossy compression. Unlike the rate-distortion function, however, it is unknown whether encoders and decoders exist that achieve the rate suggested by the RDPF. Building on results by Li and El Gamal (2018), we show that the RDPF can indeed be achieved using stochastic, variable-length codes. For this class of codes, we also prove that the RDPF lower-bounds the achievable rate