Guiding Human-Object Interactions with Rich Geometry and Relations

Human-object interaction (HOI) synthesis is crucial for creating immersive and realistic experiences for applications such as virtual reality. Existing methods often rely on simplified object representations, such as the object's centroid or the nearest point to a human, to achieve physically plausible motions. However, these approaches may overlook geometric complexity, resulting in suboptimal interaction fidelity. To address this limitation, we introduce ROG, a novel diffusion-based framework that models the spatiotemporal relationships inherent in HOIs with rich geometric detail. For efficient object representation, we select boundary-focused and fine-detail key points from the object mesh, ensuring a comprehensive depiction of the object's geometry. This representation is used to construct an interactive distance field (IDF), capturing the robust HOI dynamics. Furthermore, we develop a diffusion-based relation model that integrates spatial and temporal attention mechanisms, enabling a better understanding of intricate HOI relationships. This relation model refines the generated motion's IDF, guiding the motion generation process to produce relation-aware and semantically aligned movements. Experimental evaluations demonstrate that ROG significantly outperforms state-of-the-art methods in the realism and semantic accuracy of synthesized HOIs.

Flow-based linear embedding for Bayesian filtering of nonlinear stochastic dynamical systems

Bayesian filtering for high-dimensional nonlinear stochastic dynamical systems is a fundamental yet challenging problem in many fields of science and engineering. Existing methods face significant obstacles: Gaussian-based filters struggle with non-Gaussian distributions, sequential Monte Carlo methods are computationally intensive and prone to particle degeneracy in high dimensions, and deep learning approaches often fail to balance accuracy and efficiency in complex filtering tasks. To address these challenges, we propose a flow-based Bayesian filter (FBF) that integrates normalizing flows to construct a latent linear state-space model with Gaussian filtering distributions. This framework enables efficient density estimation and sampling through invertible transformations provided by normalizing flows, which can be learned directly from data, thereby eliminating the need for prior knowledge of system dynamics or observation models. Numerical experiments demonstrate the advantages of FBF in terms of both accuracy and efficiency.

Energy based diffusion generator for efficient sampling of Boltzmann distributions

We introduce a novel sampler called the energy based diffusion generator for generating samples from arbitrary target distributions. The sampling model employs a structure similar to a variational autoencoder, utilizing a decoder to transform latent variables from a simple distribution into random variables approximating the target distribution, and we design an encoder based on the diffusion model. Leveraging the powerful modeling capacity of the diffusion model for complex distributions, we can obtain an accurate variational estimate of the Kullback-Leibler divergence between the distributions of the generated samples and the target. Moreover, we propose a decoder based on generalized Hamiltonian dynamics to further enhance sampling performance. Through empirical evaluation, we demonstrate the effectiveness of our method across various complex distribution functions, showcasing its superiority compared to existing methods.

IB-UQ: Information bottleneck based uncertainty quantification for neural function regression and neural operator learning

In this paper, a novel framework is established for uncertainty quantification via information bottleneck (IB-UQ) for scientific machine learning tasks, including deep neural network (DNN) regression and neural operator learning (DeepONet). Specifically, we first employ the General Incompressible-Flow Networks (GIN) model to learn a "wide" distribution fromnoisy observation data. Then, following the information bottleneck objective, we learn a stochastic map from input to some latent representation that can be used to predict the output. A tractable variational bound on the IB objective is constructed with a normalizing flow reparameterization. Hence, we can optimize the objective using the stochastic gradient descent method. IB-UQ can provide both mean and variance in the label prediction by explicitly modeling the representation variables. Compared to most DNN regression methods and the deterministic DeepONet, the proposed model can be trained on noisy data and provide accurate predictions with reliable uncertainty estimates on unseen noisy data. We demonstrate the capability of the proposed IB-UQ framework via several representative examples, including discontinuous function regression, real-world dataset regression and learning nonlinear operators for diffusion-reaction partial differential equation.

Monte Carlo PINNs: deep learning approach for forward and inverse problems involving high dimensional fractional partial differential equations

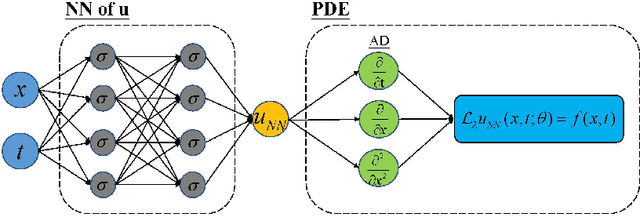
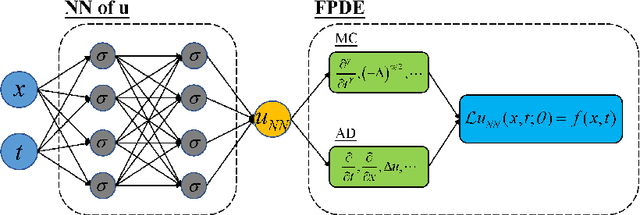
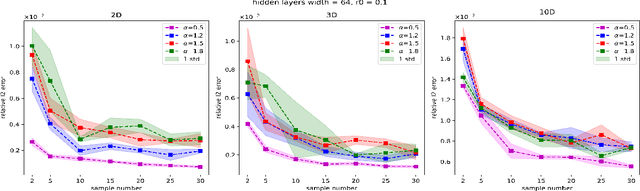
We introduce a sampling based machine learning approach, Monte Carlo physics informed neural networks (MC-PINNs), for solving forward and inverse fractional partial differential equations (FPDEs). As a generalization of physics informed neural networks (PINNs), our method relies on deep neural network surrogates in addition to a stochastic approximation strategy for computing the fractional derivatives of the DNN outputs. A key ingredient in our MC-PINNs is to construct an unbiased estimation of the physical soft constraints in the loss function. Our directly sampling approach can yield less overall computational cost compared to fPINNs proposed in \cite{pang2019fpinns} and thus provide an opportunity for solving high dimensional fractional PDEs. We validate the performance of MC-PINNs method via several examples that include high dimensional integral fractional Laplacian equations, parametric identification of time-space fractional PDEs, and fractional diffusion equation with random inputs. The results show that MC-PINNs is flexible and promising to tackle high-dimensional FPDEs.

Uncertainty Quantification in Scientific Machine Learning: Methods, Metrics, and Comparisons

Neural networks (NNs) are currently changing the computational paradigm on how to combine data with mathematical laws in physics and engineering in a profound way, tackling challenging inverse and ill-posed problems not solvable with traditional methods. However, quantifying errors and uncertainties in NN-based inference is more complicated than in traditional methods. This is because in addition to aleatoric uncertainty associated with noisy data, there is also uncertainty due to limited data, but also due to NN hyperparameters, overparametrization, optimization and sampling errors as well as model misspecification. Although there are some recent works on uncertainty quantification (UQ) in NNs, there is no systematic investigation of suitable methods towards quantifying the total uncertainty effectively and efficiently even for function approximation, and there is even less work on solving partial differential equations and learning operator mappings between infinite-dimensional function spaces using NNs. In this work, we present a comprehensive framework that includes uncertainty modeling, new and existing solution methods, as well as evaluation metrics and post-hoc improvement approaches. To demonstrate the applicability and reliability of our framework, we present an extensive comparative study in which various methods are tested on prototype problems, including problems with mixed input-output data, and stochastic problems in high dimensions. In the Appendix, we include a comprehensive description of all the UQ methods employed, which we will make available as open-source library of all codes included in this framework.

Normalizing field flows: Solving forward and inverse stochastic differential equations using physics-informed flow models

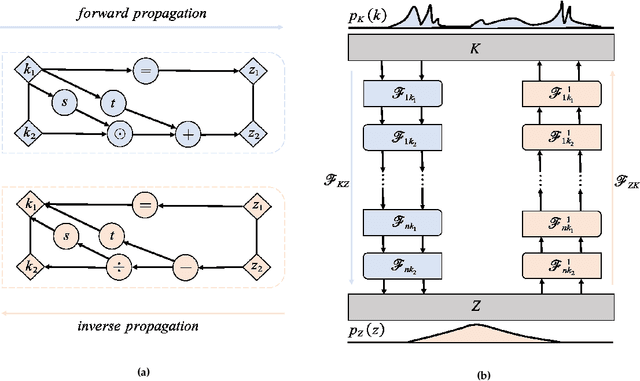
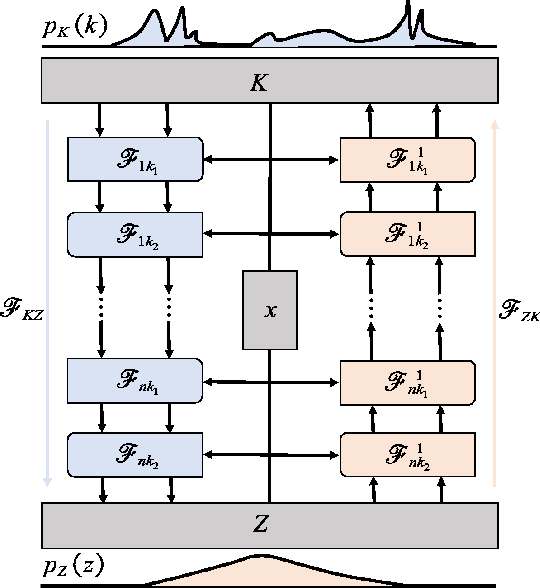
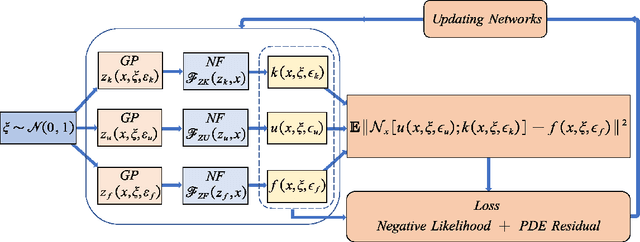
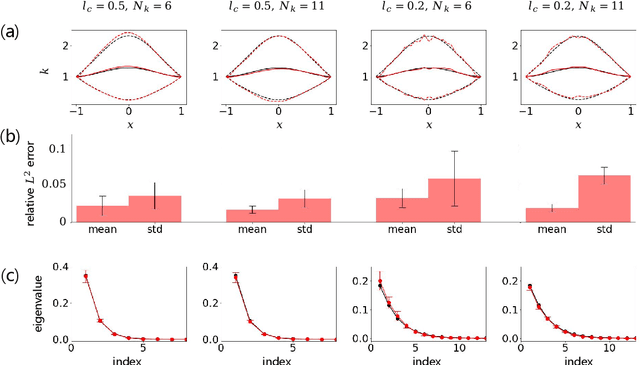
We introduce in this work the normalizing field flows (NFF) for learning random fields from scattered measurements. More precisely, we construct a bijective transformation (a normalizing flow characterizing by neural networks) between a Gaussian random field with the Karhunen-Lo\`eve (KL) expansion structure and the target stochastic field, where the KL expansion coefficients and the invertible networks are trained by maximizing the sum of the log-likelihood on scattered measurements. This NFF model can be used to solve data-driven forward, inverse, and mixed forward/inverse stochastic partial differential equations in a unified framework. We demonstrate the capability of the proposed NFF model for learning Non Gaussian processes and different types of stochastic partial differential equations.

Removable and/or Repeated Units Emerge in Overparametrized Deep Neural Networks

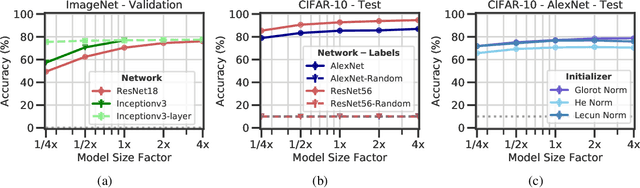
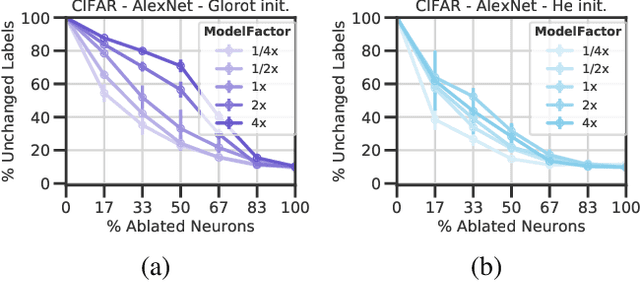
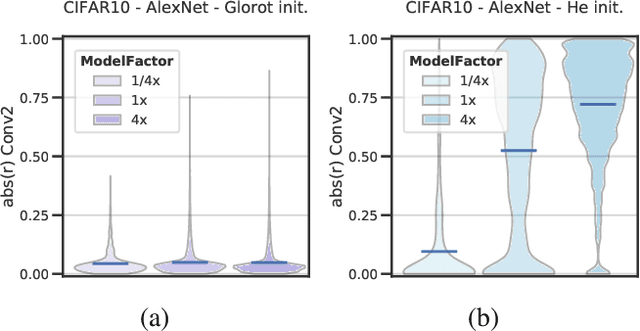
Deep neural networks (DNNs) perform well on a variety of tasks despite the fact that most networks used in practice are vastly overparametrized and even capable of perfectly fitting randomly labeled data. Recent evidence suggests that developing compressible representations is key for adjusting the complexity of overparametrized networks to the task at hand. In this paper, we provide new empirical evidence that supports this hypothesis by identifying two types of units that emerge when the network's width is increased: removable units which can be dropped out of the network without significant change to the output and repeated units whose activities are highly correlated with other units. The emergence of these units implies capacity constraints as the function the network represents could be expressed by a smaller network without these units. In a series of experiments with AlexNet, ResNet and Inception networks in the CIFAR-10 and ImageNet datasets, and also using shallow networks with synthetic data, we show that DNNs consistently increase either the number of removable units, repeated units, or both at greater widths for a comprehensive set of hyperparameters. These results suggest that the mechanisms by which networks in the deep learning regime adjust their complexity operate at the unit level and highlight the need for additional research into what drives the emergence of such units.

Learning in Modal Space: Solving Time-Dependent Stochastic PDEs Using Physics-Informed Neural Networks

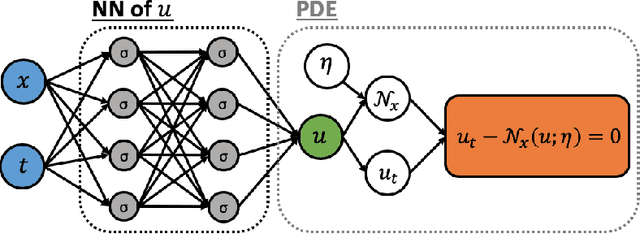
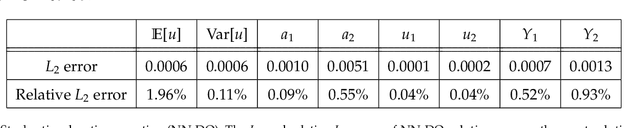
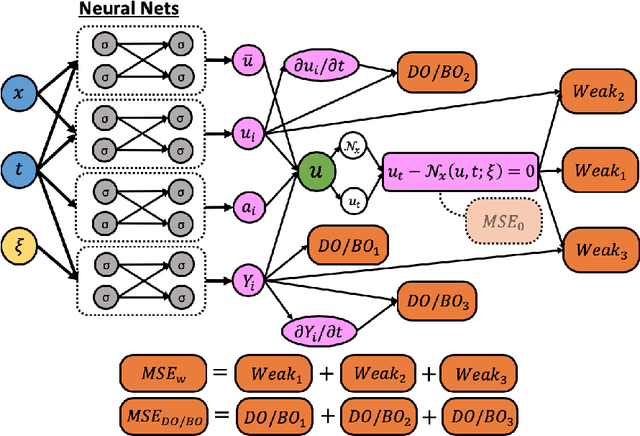
One of the open problems in scientific computing is the long-time integration of nonlinear stochastic partial differential equations (SPDEs). We address this problem by taking advantage of recent advances in scientific machine learning and the dynamically orthogonal (DO) and bi-orthogonal (BO) methods for representing stochastic processes. Specifically, we propose two new Physics-Informed Neural Networks (PINNs) for solving time-dependent SPDEs, namely the NN-DO/BO methods, which incorporate the DO/BO constraints into the loss function with an implicit form instead of generating explicit expressions for the temporal derivatives of the DO/BO modes. Hence, the proposed methods overcome some of the drawbacks of the original DO/BO methods: we do not need the assumption that the covariance matrix of the random coefficients is invertible as in the original DO method, and we can remove the assumption of no eigenvalue crossing as in the original BO method. Moreover, the NN-DO/BO methods can be used to solve time-dependent stochastic inverse problems with the same formulation and computational complexity as for forward problems. We demonstrate the capability of the proposed methods via several numerical examples: (1) A linear stochastic advection equation with deterministic initial condition where the original DO/BO method would fail; (2) Long-time integration of the stochastic Burgers' equation with many eigenvalue crossings during the whole time evolution where the original BO method fails. (3) Nonlinear reaction diffusion equation: we consider both the forward and the inverse problem, including noisy initial data, to investigate the flexibility of the NN-DO/BO methods in handling inverse and mixed type problems. Taken together, these simulation results demonstrate that the NN-DO/BO methods can be employed to effectively quantify uncertainty propagation in a wide range of physical problems.

I4U Submission to NIST SRE 2018: Leveraging from a Decade of Shared Experiences

The I4U consortium was established to facilitate a joint entry to NIST speaker recognition evaluations (SRE). The latest edition of such joint submission was in SRE 2018, in which the I4U submission was among the best-performing systems. SRE'18 also marks the 10-year anniversary of I4U consortium into NIST SRE series of evaluation. The primary objective of the current paper is to summarize the results and lessons learned based on the twelve sub-systems and their fusion submitted to SRE'18. It is also our intention to present a shared view on the advancements, progresses, and major paradigm shifts that we have witnessed as an SRE participant in the past decade from SRE'08 to SRE'18. In this regard, we have seen, among others, a paradigm shift from supervector representation to deep speaker embedding, and a switch of research challenge from channel compensation to domain adaptation.