A Variational Framework for Residual-Based Adaptivity in Neural PDE Solvers and Operator Learning

Residual-based adaptive strategies are widely used in scientific machine learning but remain largely heuristic. We introduce a unifying variational framework that formalizes these methods by integrating convex transformations of the residual. Different transformations correspond to distinct objective functionals: exponential weights target the minimization of uniform error, while linear weights recover the minimization of quadratic error. Within this perspective, adaptive weighting is equivalent to selecting sampling distributions that optimize the primal objective, thereby linking discretization choices directly to error metrics. This principled approach yields three benefits: (1) it enables systematic design of adaptive schemes across norms, (2) reduces discretization error through variance reduction of the loss estimator, and (3) enhances learning dynamics by improving the gradient signal-to-noise ratio. Extending the framework to operator learning, we demonstrate substantial performance gains across optimizers and architectures. Our results provide a theoretical justification of residual-based adaptivity and establish a foundation for principled discretization and training strategies.

Learning Turbulent Flows with Generative Models: Super-resolution, Forecasting, and Sparse Flow Reconstruction

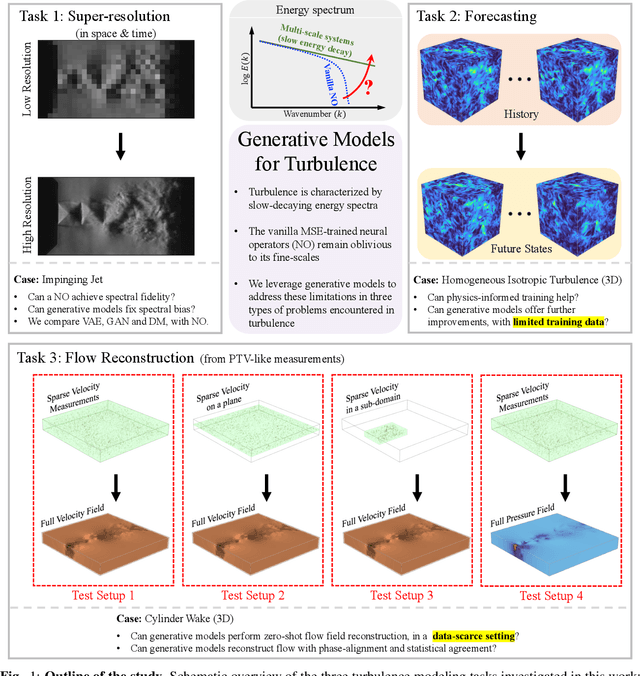
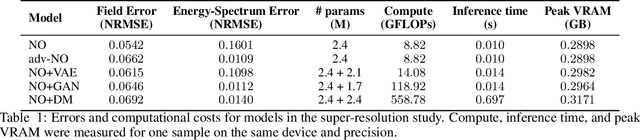
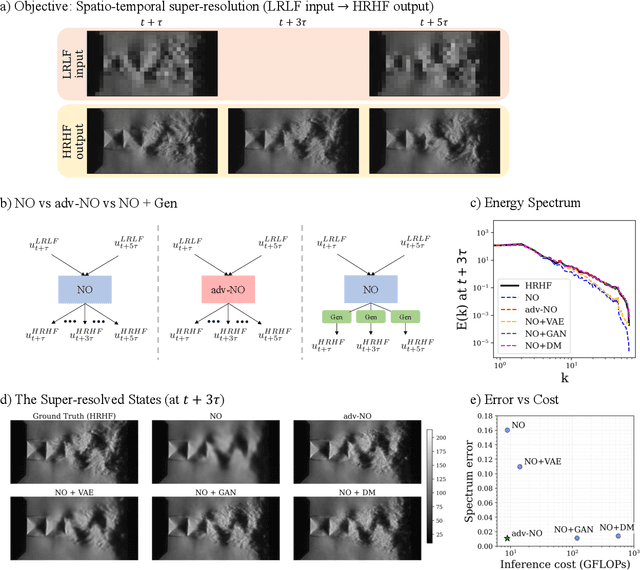
Neural operators are promising surrogates for dynamical systems but when trained with standard L2 losses they tend to oversmooth fine-scale turbulent structures. Here, we show that combining operator learning with generative modeling overcomes this limitation. We consider three practical turbulent-flow challenges where conventional neural operators fail: spatio-temporal super-resolution, forecasting, and sparse flow reconstruction. For Schlieren jet super-resolution, an adversarially trained neural operator (adv-NO) reduces the energy-spectrum error by 15x while preserving sharp gradients at neural operator-like inference cost. For 3D homogeneous isotropic turbulence, adv-NO trained on only 160 timesteps from a single trajectory forecasts accurately for five eddy-turnover times and offers 114x wall-clock speed-up at inference than the baseline diffusion-based forecasters, enabling near-real-time rollouts. For reconstructing cylinder wake flows from highly sparse Particle Tracking Velocimetry-like inputs, a conditional generative model infers full 3D velocity and pressure fields with correct phase alignment and statistics. These advances enable accurate reconstruction and forecasting at low compute cost, bringing near-real-time analysis and control within reach in experimental and computational fluid mechanics. See our project page: https://vivekoommen.github.io/Gen4Turb/

Leveraging Operator Learning to Accelerate Convergence of the Preconditioned Conjugate Gradient Method

We propose a new deflation strategy to accelerate the convergence of the preconditioned conjugate gradient(PCG) method for solving parametric large-scale linear systems of equations. Unlike traditional deflation techniques that rely on eigenvector approximations or recycled Krylov subspaces, we generate the deflation subspaces using operator learning, specifically the Deep Operator Network~(DeepONet). To this aim, we introduce two complementary approaches for assembling the deflation operators. The first approach approximates near-null space vectors of the discrete PDE operator using the basis functions learned by the DeepONet. The second approach directly leverages solutions predicted by the DeepONet. To further enhance convergence, we also propose several strategies for prescribing the sparsity pattern of the deflation operator. A comprehensive set of numerical experiments encompassing steady-state, time-dependent, scalar, and vector-valued problems posed on both structured and unstructured geometries is presented and demonstrates the effectiveness of the proposed DeepONet-based deflated PCG method, as well as its generalization across a wide range of model parameters and problem resolutions.

Representation Meets Optimization: Training PINNs and PIKANs for Gray-Box Discovery in Systems Pharmacology

Physics-Informed Kolmogorov-Arnold Networks (PIKANs) are gaining attention as an effective counterpart to the original multilayer perceptron-based Physics-Informed Neural Networks (PINNs). Both representation models can address inverse problems and facilitate gray-box system identification. However, a comprehensive understanding of their performance in terms of accuracy and speed remains underexplored. In particular, we introduce a modified PIKAN architecture, tanh-cPIKAN, which is based on Chebyshev polynomials for parametrization of the univariate functions with an extra nonlinearity for enhanced performance. We then present a systematic investigation of how choices of the optimizer, representation, and training configuration influence the performance of PINNs and PIKANs in the context of systems pharmacology modeling. We benchmark a wide range of first-order, second-order, and hybrid optimizers, including various learning rate schedulers. We use the new Optax library to identify the most effective combinations for learning gray-boxes under ill-posed, non-unique, and data-sparse conditions. We examine the influence of model architecture (MLP vs. KAN), numerical precision (single vs. double), the need for warm-up phases for second-order methods, and sensitivity to the initial learning rate. We also assess the optimizer scalability for larger models and analyze the trade-offs introduced by JAX in terms of computational efficiency and numerical accuracy. Using two representative systems pharmacology case studies - a pharmacokinetics model and a chemotherapy drug-response model - we offer practical guidance on selecting optimizers and representation models/architectures for robust and efficient gray-box discovery. Our findings provide actionable insights for improving the training of physics-informed networks in biomedical applications and beyond.

Mitigating Spectral Bias in Neural Operators via High-Frequency Scaling for Physical Systems

Neural operators have emerged as powerful surrogates for modeling complex physical problems. However, they suffer from spectral bias making them oblivious to high-frequency modes, which are present in multiscale physical systems. Therefore, they tend to produce over-smoothed solutions, which is particularly problematic in modeling turbulence and for systems with intricate patterns and sharp gradients such as multi-phase flow systems. In this work, we introduce a new approach named high-frequency scaling (HFS) to mitigate spectral bias in convolutional-based neural operators. By integrating HFS with proper variants of UNet neural operators, we demonstrate a higher prediction accuracy by mitigating spectral bias in single and two-phase flow problems. Unlike Fourier-based techniques, HFS is directly applied to the latent space, thus eliminating the computational cost associated with the Fourier transform. Additionally, we investigate alternative spectral bias mitigation through diffusion models conditioned on neural operators. While the diffusion model integrated with the standard neural operator may still suffer from significant errors, these errors are substantially reduced when the diffusion model is integrated with a HFS-enhanced neural operator.

Learning and discovering multiple solutions using physics-informed neural networks with random initialization and deep ensemble

We explore the capability of physics-informed neural networks (PINNs) to discover multiple solutions. Many real-world phenomena governed by nonlinear differential equations (DEs), such as fluid flow, exhibit multiple solutions under the same conditions, yet capturing this solution multiplicity remains a significant challenge. A key difficulty is giving appropriate initial conditions or initial guesses, to which the widely used time-marching schemes and Newton's iteration method are very sensitive in finding solutions for complex computational problems. While machine learning models, particularly PINNs, have shown promise in solving DEs, their ability to capture multiple solutions remains underexplored. In this work, we propose a simple and practical approach using PINNs to learn and discover multiple solutions. We first reveal that PINNs, when combined with random initialization and deep ensemble method -- originally developed for uncertainty quantification -- can effectively uncover multiple solutions to nonlinear ordinary and partial differential equations (ODEs/PDEs). Our approach highlights the critical role of initialization in shaping solution diversity, addressing an often-overlooked aspect of machine learning for scientific computing. Furthermore, we propose utilizing PINN-generated solutions as initial conditions or initial guesses for conventional numerical solvers to enhance accuracy and efficiency in capturing multiple solutions. Extensive numerical experiments, including the Allen-Cahn equation and cavity flow, where our approach successfully identifies both stable and unstable solutions, validate the effectiveness of our method. These findings establish a general and efficient framework for addressing solution multiplicity in nonlinear differential equations.

DeepSeek vs. ChatGPT: A Comparative Study for Scientific Computing and Scientific Machine Learning Tasks

Large Language Models (LLMs) have emerged as powerful tools for tackling a wide range of problems, including those in scientific computing, particularly in solving partial differential equations (PDEs). However, different models exhibit distinct strengths and preferences, resulting in varying levels of performance. In this paper, we compare the capabilities of the most advanced LLMs--ChatGPT and DeepSeek--along with their reasoning-optimized versions in addressing computational challenges. Specifically, we evaluate their proficiency in solving traditional numerical problems in scientific computing as well as leveraging scientific machine learning techniques for PDE-based problems. We designed all our experiments so that a non-trivial decision is required, e.g. defining the proper space of input functions for neural operator learning. Our findings reveal that the latest model, ChatGPT o3-mini-high, usually delivers the most accurate results while also responding significantly faster than its reasoning counterpart, DeepSeek R1. This enhanced speed and accuracy make ChatGPT o3-mini-high a more practical and efficient choice for diverse computational tasks at this juncture.

Connecting the geometry and dynamics of many-body complex systems with message passing neural operators

The relationship between scale transformations and dynamics established by renormalization group techniques is a cornerstone of modern physical theories, from fluid mechanics to elementary particle physics. Integrating renormalization group methods into neural operators for many-body complex systems could provide a foundational inductive bias for learning their effective dynamics, while also uncovering multiscale organization. We introduce a scalable AI framework, ROMA (Renormalized Operators with Multiscale Attention), for learning multiscale evolution operators of many-body complex systems. In particular, we develop a renormalization procedure based on neural analogs of the geometric and laplacian renormalization groups, which can be co-learned with neural operators. An attention mechanism is used to model multiscale interactions by connecting geometric representations of local subgraphs and dynamical operators. We apply this framework in challenging conditions: large systems of more than 1M nodes, long-range interactions, and noisy input-output data for two contrasting examples: Kuramoto oscillators and Burgers-like social dynamics. We demonstrate that the ROMA framework improves scalability and positive transfer between forecasting and effective dynamics tasks compared to state-of-the-art operator learning techniques, while also giving insight into multiscale interactions. Additionally, we investigate power law scaling in the number of model parameters, and demonstrate a departure from typical power law exponents in the presence of hierarchical and multiscale interactions.

Automatic selection of the best neural architecture for time series forecasting via multi-objective optimization and Pareto optimality conditions

Time series forecasting plays a pivotal role in a wide range of applications, including weather prediction, healthcare, structural health monitoring, predictive maintenance, energy systems, and financial markets. While models such as LSTM, GRU, Transformers, and State-Space Models (SSMs) have become standard tools in this domain, selecting the optimal architecture remains a challenge. Performance comparisons often depend on evaluation metrics and the datasets under analysis, making the choice of a universally optimal model controversial. In this work, we introduce a flexible automated framework for time series forecasting that systematically designs and evaluates diverse network architectures by integrating LSTM, GRU, multi-head Attention, and SSM blocks. Using a multi-objective optimization approach, our framework determines the number, sequence, and combination of blocks to align with specific requirements and evaluation objectives. From the resulting Pareto-optimal architectures, the best model for a given context is selected via a user-defined preference function. We validate our framework across four distinct real-world applications. Results show that a single-layer GRU or LSTM is usually optimal when minimizing training time alone. However, when maximizing accuracy or balancing multiple objectives, the best architectures are often composite designs incorporating multiple block types in specific configurations. By employing a weighted preference function, users can resolve trade-offs between objectives, revealing novel, context-specific optimal architectures. Our findings underscore that no single neural architecture is universally optimal for time series forecasting. Instead, the best-performing model emerges as a data-driven composite architecture tailored to user-defined criteria and evaluation objectives.

Scalable Bayesian Physics-Informed Kolmogorov-Arnold Networks

Uncertainty quantification (UQ) plays a pivotal role in scientific machine learning, especially when surrogate models are used to approximate complex systems. Although multilayer perceptions (MLPs) are commonly employed as surrogates, they often suffer from overfitting due to their large number of parameters. Kolmogorov-Arnold networks (KANs) offer an alternative solution with fewer parameters. However, gradient-based inference methods, such as Hamiltonian Monte Carlo (HMC), may result in computational inefficiency when applied to KANs, especially for large-scale datasets, due to the high cost of back-propagation.To address these challenges, we propose a novel approach, combining the dropout Tikhonov ensemble Kalman inversion (DTEKI) with Chebyshev KANs. This gradient-free method effectively mitigates overfitting and enhances numerical stability. Additionally, we incorporate the active subspace method to reduce the parameter-space dimensionality, allowing us to improve the accuracy of predictions and obtain more reliable uncertainty estimates.Extensive experiments demonstrate the efficacy of our approach in various test cases, including scenarios with large datasets and high noise levels. Our results show that the new method achieves comparable or better accuracy, much higher efficiency as well as stability compared to HMC, in addition to scalability. Moreover, by leveraging the low-dimensional parameter subspace, our method preserves prediction accuracy while substantially reducing further the computational cost.