Merge to Mix: Mixing Datasets via Model Merging

Mixing datasets for fine-tuning large models (LMs) has become critical for maximizing performance on downstream tasks. However, composing effective dataset mixtures typically relies on heuristics and trial-and-error, often requiring multiple fine-tuning runs to achieve the desired outcome. We propose a novel method, $\textit{Merge to Mix}$, that accelerates composing dataset mixtures through model merging. Model merging is a recent technique that combines the abilities of multiple individually fine-tuned LMs into a single LM by using a few simple arithmetic operations. Our key insight is that merging models individually fine-tuned on each dataset in a mixture can effectively serve as a surrogate for a model fine-tuned on the entire mixture. Merge to Mix leverages this insight to accelerate selecting dataset mixtures without requiring full fine-tuning on each candidate mixture. Our experiments demonstrate that Merge to Mix surpasses state-of-the-art methods in dataset selection for fine-tuning LMs.

Removable and/or Repeated Units Emerge in Overparametrized Deep Neural Networks

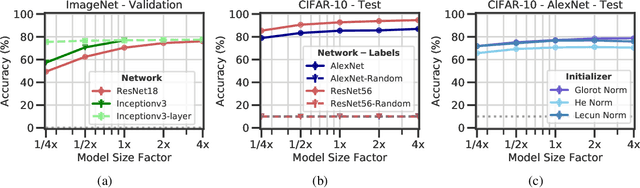
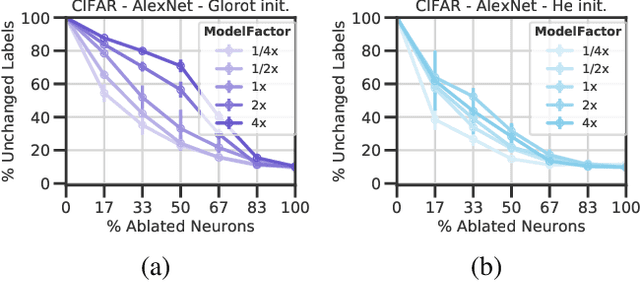
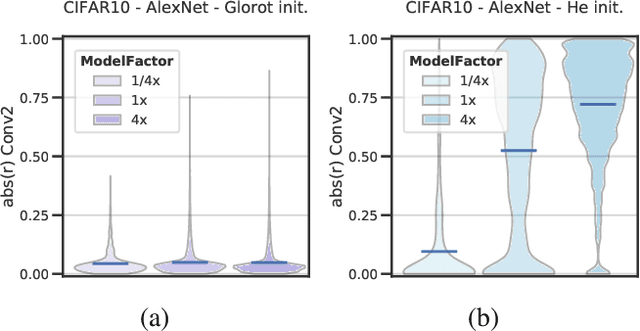
Deep neural networks (DNNs) perform well on a variety of tasks despite the fact that most networks used in practice are vastly overparametrized and even capable of perfectly fitting randomly labeled data. Recent evidence suggests that developing compressible representations is key for adjusting the complexity of overparametrized networks to the task at hand. In this paper, we provide new empirical evidence that supports this hypothesis by identifying two types of units that emerge when the network's width is increased: removable units which can be dropped out of the network without significant change to the output and repeated units whose activities are highly correlated with other units. The emergence of these units implies capacity constraints as the function the network represents could be expressed by a smaller network without these units. In a series of experiments with AlexNet, ResNet and Inception networks in the CIFAR-10 and ImageNet datasets, and also using shallow networks with synthetic data, we show that DNNs consistently increase either the number of removable units, repeated units, or both at greater widths for a comprehensive set of hyperparameters. These results suggest that the mechanisms by which networks in the deep learning regime adjust their complexity operate at the unit level and highlight the need for additional research into what drives the emergence of such units.