Automatic Depression Detection: An Emotional Audio-Textual Corpus and a GRU/BiLSTM-based Model

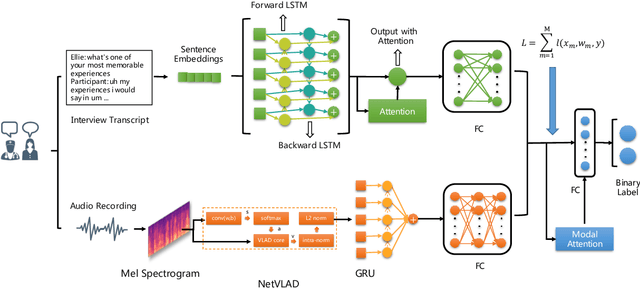
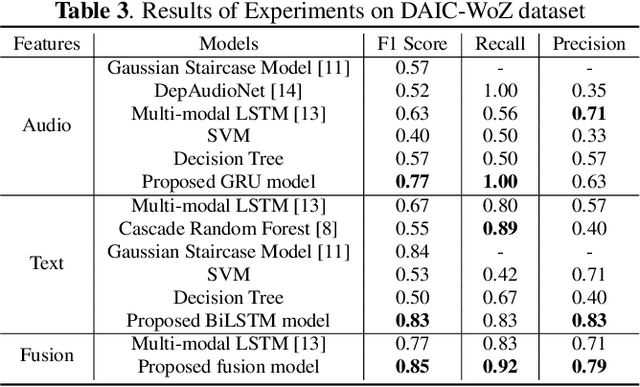
Depression is a global mental health problem, the worst case of which can lead to suicide. An automatic depression detection system provides great help in facilitating depression self-assessment and improving diagnostic accuracy. In this work, we propose a novel depression detection approach utilizing speech characteristics and linguistic contents from participants' interviews. In addition, we establish an Emotional Audio-Textual Depression Corpus (EATD-Corpus) which contains audios and extracted transcripts of responses from depressed and non-depressed volunteers. To the best of our knowledge, EATD-Corpus is the first and only public depression dataset that contains audio and text data in Chinese. Evaluated on two depression datasets, the proposed method achieves the state-of-the-art performances. The outperforming results demonstrate the effectiveness and generalization ability of the proposed method. The source code and EATD-Corpus are available at https://github.com/speechandlanguageprocessing/ICASSP2022-Depression.

Explicitly antisymmetrized neural network layers for variational Monte Carlo simulation

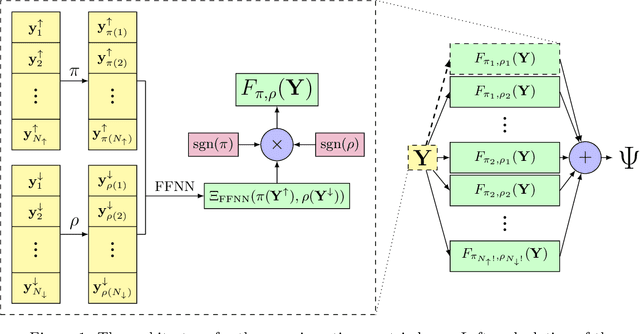
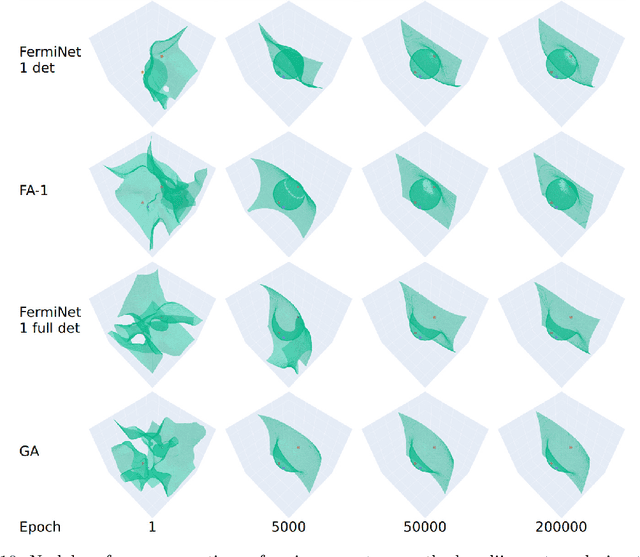
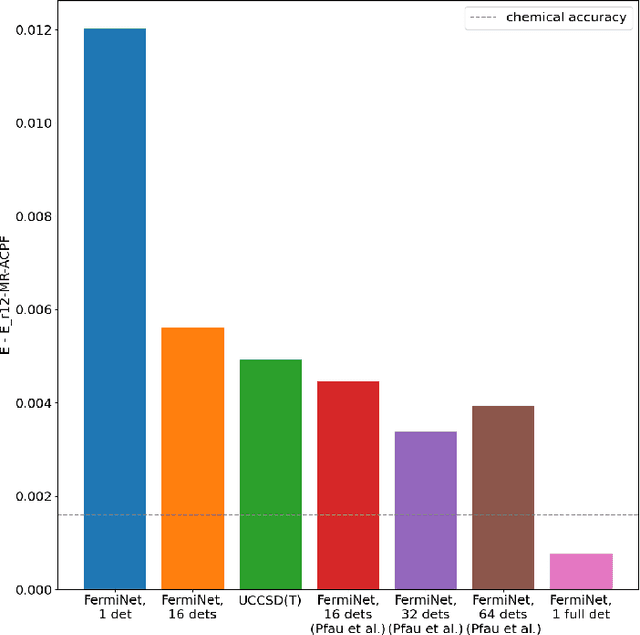
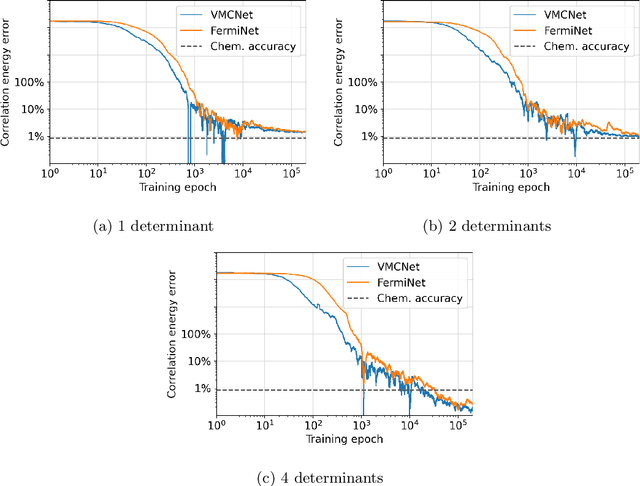
The combination of neural networks and quantum Monte Carlo methods has arisen as a path forward for highly accurate electronic structure calculations. Previous proposals have combined equivariant neural network layers with an antisymmetric layer to satisfy the antisymmetry requirements of the electronic wavefunction. However, to date it is unclear if one can represent antisymmetric functions of physical interest, and it is difficult to measure the expressiveness of the antisymmetric layer. This work attempts to address this problem by introducing explicitly antisymmetrized universal neural network layers as a diagnostic tool. We first introduce a generic antisymmetric (GA) layer, which we use to replace the entire antisymmetric layer of the highly accurate ansatz known as the FermiNet. We demonstrate that the resulting FermiNet-GA architecture can yield effectively the exact ground state energy for small systems. We then consider a factorized antisymmetric (FA) layer which more directly generalizes the FermiNet by replacing products of determinants with products of antisymmetrized neural networks. Interestingly, the resulting FermiNet-FA architecture does not outperform the FermiNet. This suggests that the sum of products of antisymmetries is a key limiting aspect of the FermiNet architecture. To explore this further, we investigate a slight modification of the FermiNet called the full determinant mode, which replaces each product of determinants with a single combined determinant. The full single-determinant FermiNet closes a large part of the gap between the standard single-determinant FermiNet and FermiNet-GA. Surprisingly, on the nitrogen molecule at a dissociating bond length of 4.0 Bohr, the full single-determinant FermiNet can significantly outperform the standard 64-determinant FermiNet, yielding an energy within 0.4 kcal/mol of the best available computational benchmark.

Integrative Clustering of Multi-View Data by Nonnegative Matrix Factorization

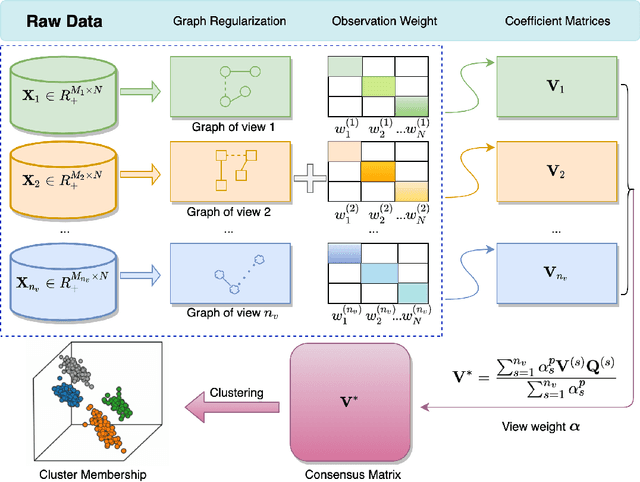
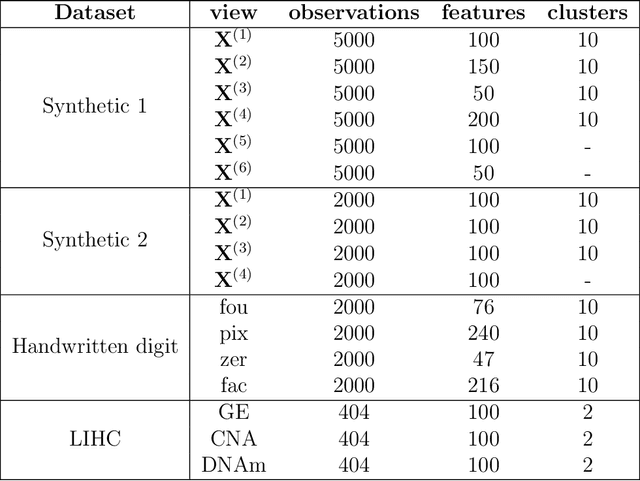
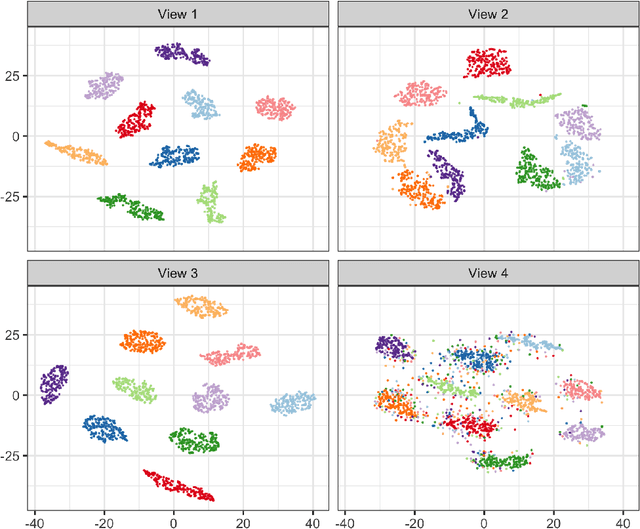
Learning multi-view data is an emerging problem in machine learning research, and nonnegative matrix factorization (NMF) is a popular dimensionality-reduction method for integrating information from multiple views. These views often provide not only consensus but also diverse information. However, most multi-view NMF algorithms assign equal weight to each view or tune the weight via line search empirically, which can be computationally expensive or infeasible without any prior knowledge of the views. In this paper, we propose a weighted multi-view NMF (WM-NMF) algorithm. In particular, we aim to address the critical technical gap, which is to learn both view-specific and observation-specific weights to quantify each view's information content. The introduced weighting scheme can alleviate unnecessary views' adverse effects and enlarge the positive effects of the important views by assigning smaller and larger weights, respectively. In addition, we provide theoretical investigations about the convergence, perturbation analysis, and generalization error of the WM-NMF algorithm. Experimental results confirm the effectiveness and advantages of the proposed algorithm in terms of achieving better clustering performance and dealing with the corrupted data compared to the existing algorithms.

Mixture of Linear Models Co-supervised by Deep Neural Networks

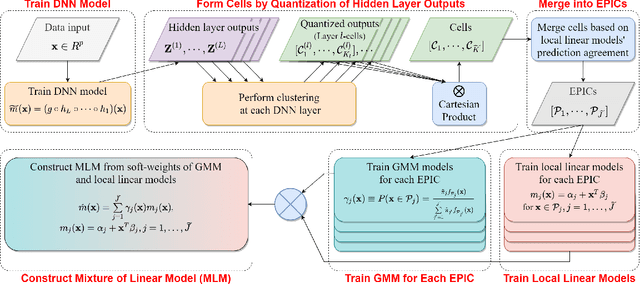
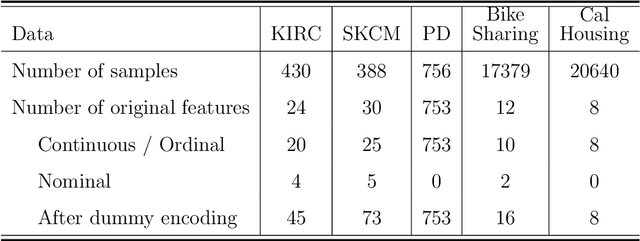
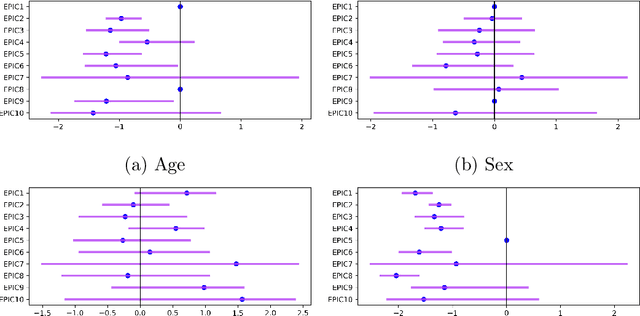
Deep neural network (DNN) models have achieved phenomenal success for applications in many domains, ranging from academic research in science and engineering to industry and business. The modeling power of DNN is believed to have come from the complexity and over-parameterization of the model, which on the other hand has been criticized for the lack of interpretation. Although certainly not true for every application, in some applications, especially in economics, social science, healthcare industry, and administrative decision making, scientists or practitioners are resistant to use predictions made by a black-box system for multiple reasons. One reason is that a major purpose of a study can be to make discoveries based upon the prediction function, e.g., to reveal the relationships between measurements. Another reason can be that the training dataset is not large enough to make researchers feel completely sure about a purely data-driven result. Being able to examine and interpret the prediction function will enable researchers to connect the result with existing knowledge or gain insights about new directions to explore. Although classic statistical models are much more explainable, their accuracy often falls considerably below DNN. In this paper, we propose an approach to fill the gap between relatively simple explainable models and DNN such that we can more flexibly tune the trade-off between interpretability and accuracy. Our main idea is a mixture of discriminative models that is trained with the guidance from a DNN. Although mixtures of discriminative models have been studied before, our way of generating the mixture is quite different.

Filters for ISI Suppression in Molecular Communication via Diffusion

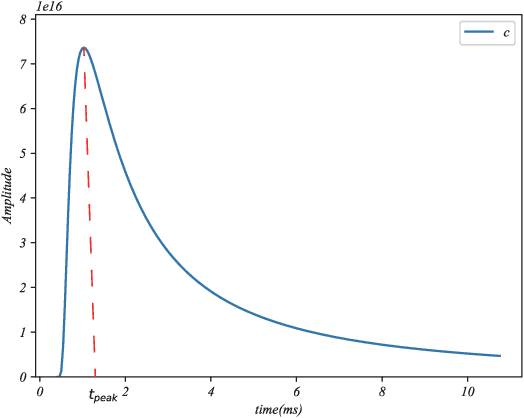
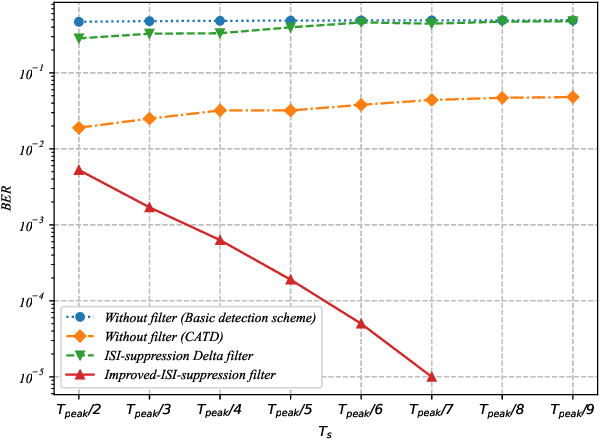
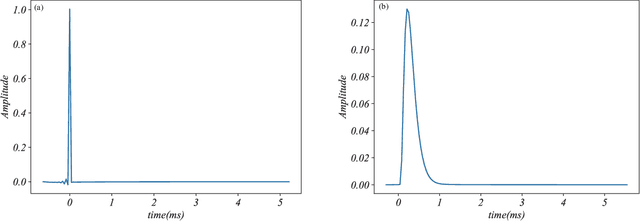
Molecular communication via diffusion (MCvD) is considered as one of the most feasible communication paradigms for nanonetworks, especially for bio-nanonetworks which are usually in water-rich biological environments. Two effects that deteriorates the signal in MCvD are noise and inter-symbol interference (ISI). The expected channel impulse response of MCvD has a long and slow attenuating tail due to molecular diffusion which causes ISI and further limits the slow data rate of MCvD. The extent that ISI and noise are suppressed in an MCvD system determines its effectiveness, especially at a high data rate. Although ISI-suppression approaches have been investigated, most of them are addressed as non-essential parts in other topics, such as signal detection or modulation. Furthermore, most of the state-of-the-art ISI-suppression approaches are performed by subtracting the estimated ISI from the total signal. In this work, we investigate ISI-suppression from a new perspective of filters to filter ISI out without any ISI estimation. The principles for a good design of ISI-suppression filters in MCvD are investigated. Based on the principles, an ISI-suppression filter with good anti-noise capability and an associated signal detection scheme is proposed for MCvD scenarios with both ISI and noise. We compare the proposed scheme with the state-of-the-art ISI-suppression approaches. The result manifests that the proposed ISI-suppression scheme could recover signals deteriorated severely by both ISI and noise, which could not be effectively detected by the state-of-the-art ISI-suppression approaches.

NeurT-FDR: Controlling FDR by Incorporating Feature Hierarchy

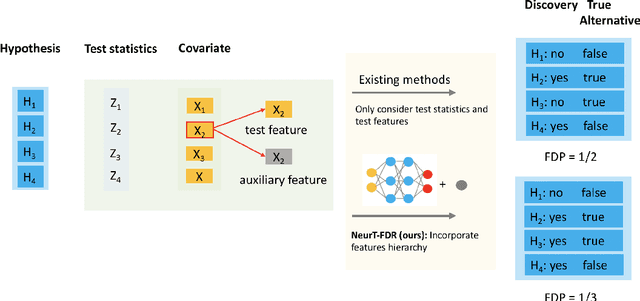
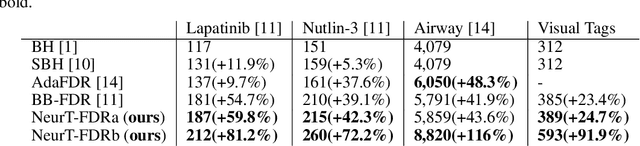
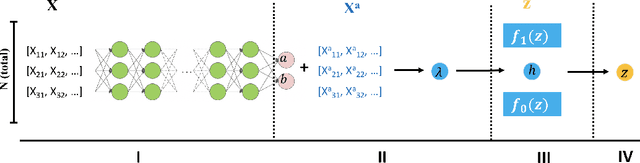
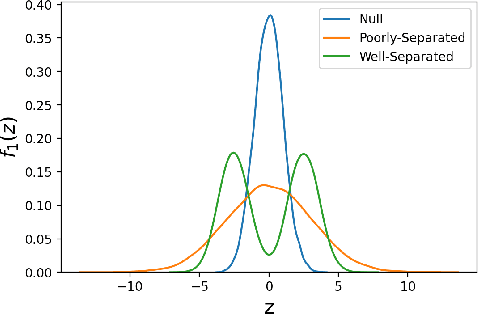
Controlling false discovery rate (FDR) while leveraging the side information of multiple hypothesis testing is an emerging research topic in modern data science. Existing methods rely on the test-level covariates while ignoring possible hierarchy among the covariates. This strategy may not be optimal for complex large-scale problems, where hierarchical information often exists among those test-level covariates. We propose NeurT-FDR which boosts statistical power and controls FDR for multiple hypothesis testing while leveraging the hierarchy among test-level covariates. Our method parametrizes the test-level covariates as a neural network and adjusts the feature hierarchy through a regression framework, which enables flexible handling of high-dimensional features as well as efficient end-to-end optimization. We show that NeurT-FDR has strong FDR guarantees and makes substantially more discoveries in synthetic and real datasets compared to competitive baselines.

Noise-Robust End-to-End Quantum Control using Deep Autoregressive Policy Networks

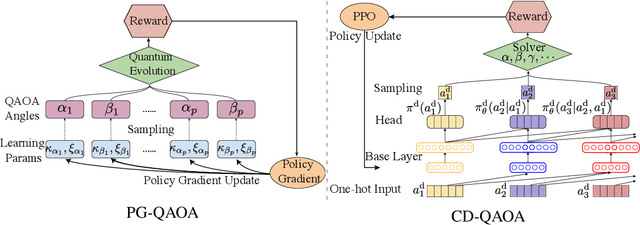
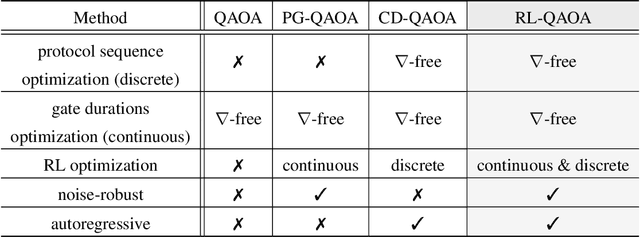
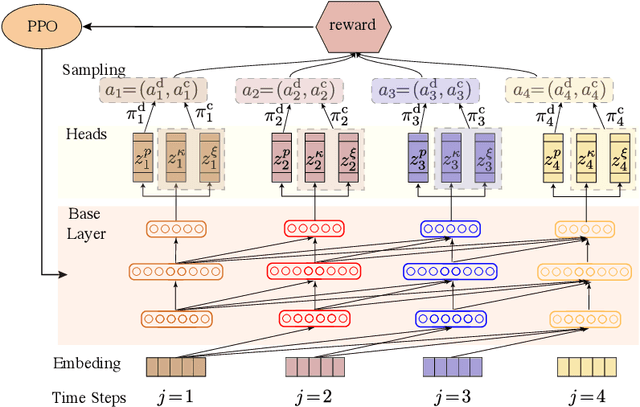
Variational quantum eigensolvers have recently received increased attention, as they enable the use of quantum computing devices to find solutions to complex problems, such as the ground energy and ground state of strongly-correlated quantum many-body systems. In many applications, it is the optimization of both continuous and discrete parameters that poses a formidable challenge. Using reinforcement learning (RL), we present a hybrid policy gradient algorithm capable of simultaneously optimizing continuous and discrete degrees of freedom in an uncertainty-resilient way. The hybrid policy is modeled by a deep autoregressive neural network to capture causality. We employ the algorithm to prepare the ground state of the nonintegrable quantum Ising model in a unitary process, parametrized by a generalized quantum approximate optimization ansatz: the RL agent solves the discrete combinatorial problem of constructing the optimal sequences of unitaries out of a predefined set and, at the same time, it optimizes the continuous durations for which these unitaries are applied. We demonstrate the noise-robust features of the agent by considering three sources of uncertainty: classical and quantum measurement noise, and errors in the control unitary durations. Our work exhibits the beneficial synergy between reinforcement learning and quantum control.

Efficient Long-Range Convolutions for Point Clouds

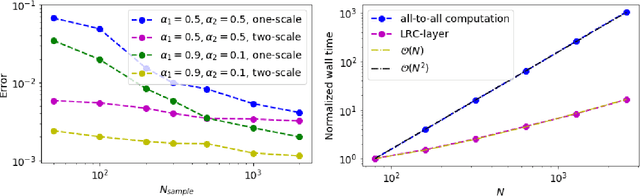
The efficient treatment of long-range interactions for point clouds is a challenging problem in many scientific machine learning applications. To extract global information, one usually needs a large window size, a large number of layers, and/or a large number of channels. This can often significantly increase the computational cost. In this work, we present a novel neural network layer that directly incorporates long-range information for a point cloud. This layer, dubbed the long-range convolutional (LRC)-layer, leverages the convolutional theorem coupled with the non-uniform Fourier transform. In a nutshell, the LRC-layer mollifies the point cloud to an adequately sized regular grid, computes its Fourier transform, multiplies the result by a set of trainable Fourier multipliers, computes the inverse Fourier transform, and finally interpolates the result back to the point cloud. The resulting global all-to-all convolution operation can be performed in nearly-linear time asymptotically with respect to the number of input points. The LRC-layer is a particularly powerful tool when combined with local convolution as together they offer efficient and seamless treatment of both short and long range interactions. We showcase this framework by introducing a neural network architecture that combines LRC-layers with short-range convolutional layers to accurately learn the energy and force associated with a $N$-body potential. We also exploit the induced two-level decomposition and propose an efficient strategy to train the combined architecture with a reduced number of samples.

Reinforcement Learning for Many-Body Ground State Preparation based on Counter-Diabatic Driving

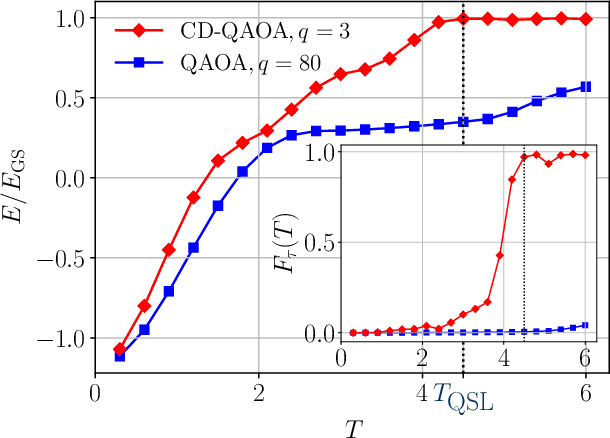
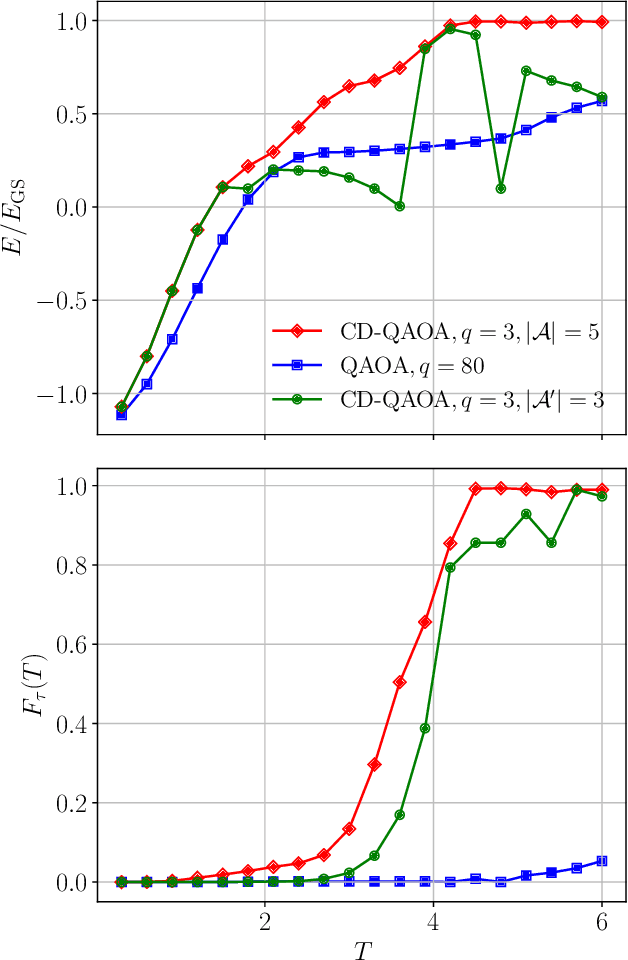
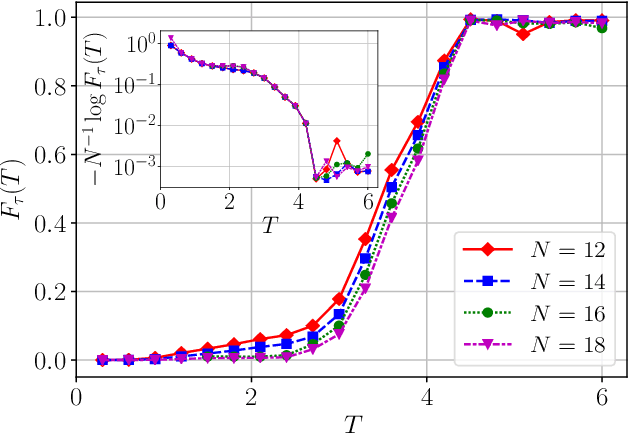
The Quantum Approximate Optimization Ansatz (QAOA) is a prominent example of variational quantum algorithms. We propose a generalized QAOA ansatz called CD-QAOA, which is inspired by the counter-diabatic (CD) driving procedure, designed for quantum many-body systems, and optimized using a reinforcement learning (RL) approach. The resulting hybrid control algorithm proves versatile in preparing the ground state of quantum-chaotic many-body spin chains, by minimizing the energy. We show that using terms occurring in the adiabatic gauge potential as additional control unitaries, it is possible to achieve fast high-fidelity many-body control away from the adiabatic regime. While each unitary retains the conventional QAOA-intrinsic continuous control degree of freedom such as the time duration, we take into account the order of the multiple available unitaries appearing in the control sequence as an additional discrete optimization problem. Endowing the policy gradient algorithm with an autoregressive deep learning architecture to capture causality, we train the RL agent to construct optimal sequences of unitaries. The algorithm has no access to the quantum state, and we find that the protocol learned on small systems may generalize to larger systems. By scanning a range of protocol durations, we present numerical evidence for a finite quantum speed limit in the nonintegrable mixed-field spin-1/2 Ising model, and for the suitability of the ansatz to prepare ground states of the spin-1 Heisenberg chain in the long-range and topologically ordered parameter regimes. This work paves the way to incorporate recent success from deep learning for the purpose of quantum many-body control.

Deep Latent Variable Model for Longitudinal Group Factor Analysis

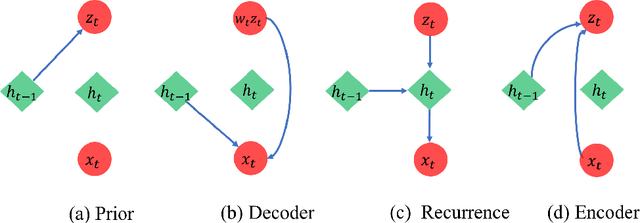
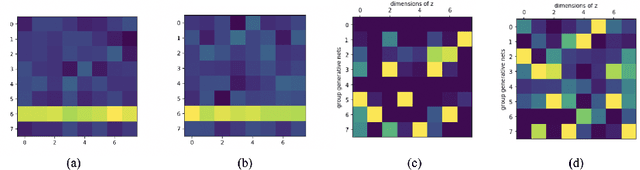
In many scientific problems such as video surveillance, modern genomic analysis, and clinical studies, data are often collected from diverse domains across time that exhibit time-dependent heterogeneous properties. It is important to not only integrate data from multiple sources (called multiview data), but also to incorporate time dependency for deep understanding of the underlying system. Latent factor models are popular tools for exploring multi-view data. However, it is frequently observed that these models do not perform well for complex systems and they are not applicable to time-series data. Therefore, we propose a generative model based on variational autoencoder and recurrent neural network to infer the latent dynamic factors for multivariate timeseries data. This approach allows us to identify the disentangled latent embeddings across multiple modalities while accounting for the time factor. We invoke our proposed model for analyzing three datasets on which we demonstrate the effectiveness and the interpretability of the model.