Fast quantum learning with statistical guarantees

Within the framework of statistical learning theory it is possible to bound the minimum number of samples required by a learner to reach a target accuracy. We show that if the bound on the accuracy is taken into account, quantum machine learning algorithms -- for which statistical guarantees are available -- cannot achieve polylogarithmic runtimes in the input dimension. This calls for a careful revaluation of quantum speedups for learning problems, even in cases where quantum access to the data is naturally available.

Approximating Hamiltonian dynamics with the Nyström method

Simulating the time-evolution of quantum mechanical systems is BQP-hard and expected to be one of the foremost applications of quantum computers. We consider the approximation of Hamiltonian dynamics using subsampling methods from randomized numerical linear algebra. We propose conditions for the efficient approximation of state vectors evolving under a given Hamiltonian. As an immediate application, we show that sample based quantum simulation, a type of evolution where the Hamiltonian is a density matrix, can be efficiently classically simulated under specific structural conditions. Our main technical contribution is a randomized algorithm for approximating Hermitian matrix exponentials. The proof leverages the Nystr\"om method to obtain low-rank approximations of the Hamiltonian. We envisage that techniques from randomized linear algebra will bring further insights into the power of quantum computation.

Learning hard quantum distributions with variational autoencoders

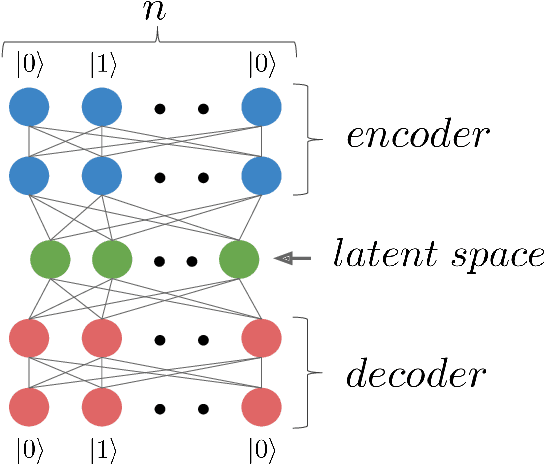
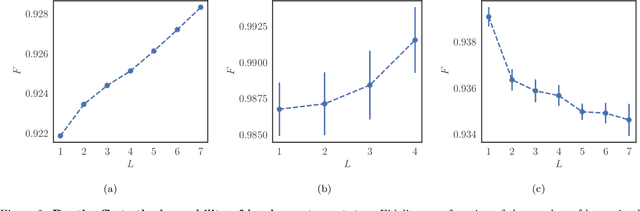
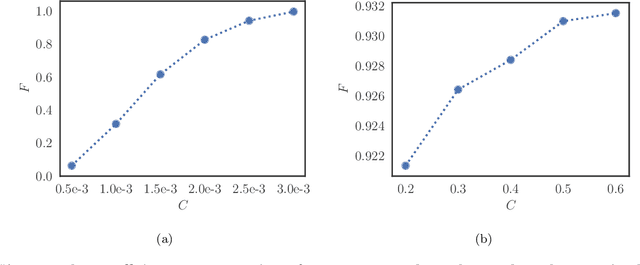
Studying general quantum many-body systems is one of the major challenges in modern physics because it requires an amount of computational resources that scales exponentially with the size of the system.Simulating the evolution of a state, or even storing its description, rapidly becomes intractable for exact classical algorithms. Recently, machine learning techniques, in the form of restricted Boltzmann machines, have been proposed as a way to efficiently represent certain quantum states with applications in state tomography and ground state estimation. Here, we introduce a new representation of states based on variational autoencoders. Variational autoencoders are a type of generative model in the form of a neural network. We probe the power of this representation by encoding probability distributions associated with states from different classes. Our simulations show that deep networks give a better representation for states that are hard to sample from, while providing no benefit for random states. This suggests that the probability distributions associated to hard quantum states might have a compositional structure that can be exploited by layered neural networks. Specifically, we consider the learnability of a class of quantum states introduced by Fefferman and Umans. Such states are provably hard to sample for classical computers, but not for quantum ones, under plausible computational complexity assumptions. The good level of compression achieved for hard states suggests these methods can be suitable for characterising states of the size expected in first generation quantum hardware.

Stabiliser states are efficiently PAC-learnable

The exponential scaling of the wave function is a fundamental property of quantum systems with far reaching implications in our ability to process quantum information. A problem where these are particularly relevant is quantum state tomography. State tomography, whose objective is to obtain a full description of a quantum system, can be analysed in the framework of computational learning theory. In this model, quantum states have been shown to be Probably Approximately Correct (PAC)-learnable with sample complexity linear in the number of qubits. However, it is conjectured that in general quantum states require an exponential amount of computation to be learned. Here, using results from the literature on the efficient classical simulation of quantum systems, we show that stabiliser states are efficiently PAC-learnable. Our results solve an open problem formulated by Aaronson [Proc. R. Soc. A, 2088, (2007)] and propose learning theory as a tool for exploring the power of quantum computation.

Learning DNFs under product distributions via μ-biased quantum Fourier sampling

We show that DNF formulae can be quantum PAC-learned in polynomial time under product distributions using a quantum example oracle. The best classical algorithm (without access to membership queries) runs in superpolynomial time. Our result extends the work by Bshouty and Jackson (1998) that proved that DNF formulae are efficiently learnable under the uniform distribution using a quantum example oracle. Our proof is based on a new quantum algorithm that efficiently samples the coefficients of a {\mu}-biased Fourier transform.

Quantum machine learning: a classical perspective

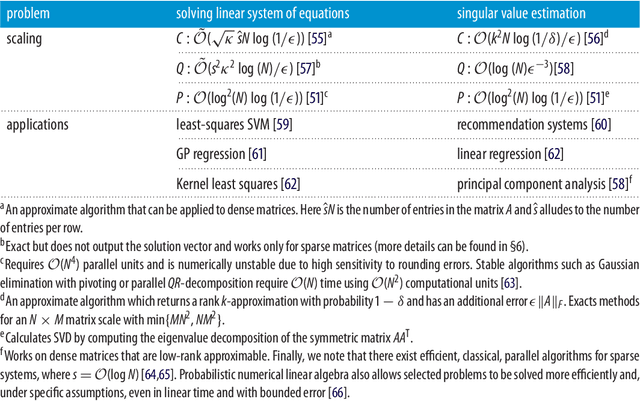
Recently, increased computational power and data availability, as well as algorithmic advances, have led machine learning techniques to impressive results in regression, classification, data-generation and reinforcement learning tasks. Despite these successes, the proximity to the physical limits of chip fabrication alongside the increasing size of datasets are motivating a growing number of researchers to explore the possibility of harnessing the power of quantum computation to speed-up classical machine learning algorithms. Here we review the literature in quantum machine learning and discuss perspectives for a mixed readership of classical machine learning and quantum computation experts. Particular emphasis will be placed on clarifying the limitations of quantum algorithms, how they compare with their best classical counterparts and why quantum resources are expected to provide advantages for learning problems. Learning in the presence of noise and certain computationally hard problems in machine learning are identified as promising directions for the field. Practical questions, like how to upload classical data into quantum form, will also be addressed.

Experimental learning of quantum states

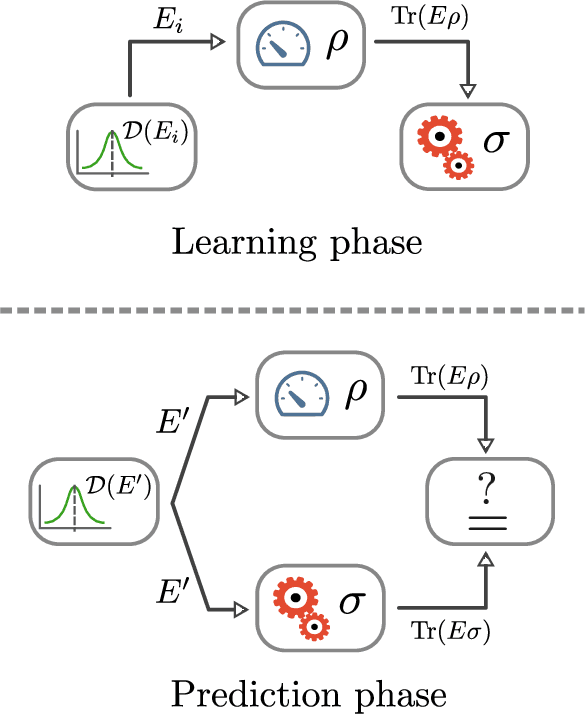
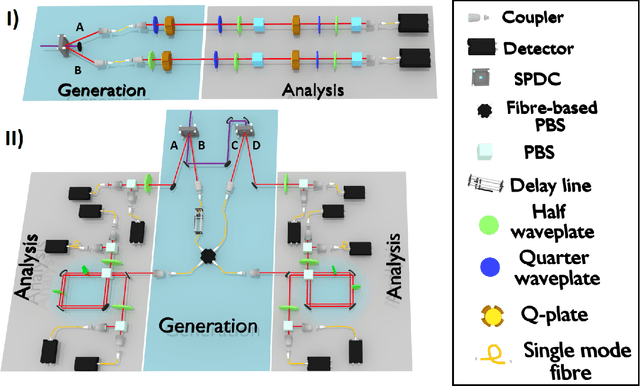
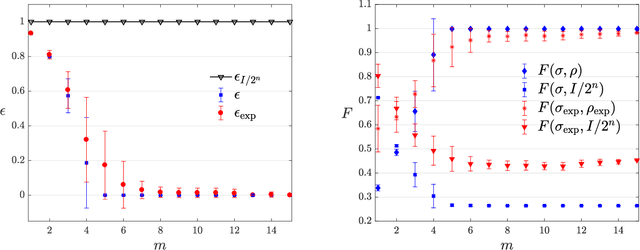
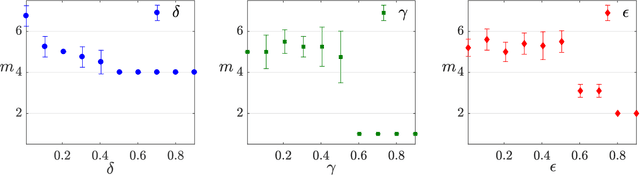
The number of parameters describing a quantum state is well known to grow exponentially with the number of particles. This scaling clearly limits our ability to do tomography to systems with no more than a few qubits and has been used to argue against the universal validity of quantum mechanics itself. However, from a computational learning theory perspective, it can be shown that, in a probabilistic setting, quantum states can be approximately learned using only a linear number of measurements. Here we experimentally demonstrate this linear scaling in optical systems with up to 6 qubits. Our results highlight the power of computational learning theory to investigate quantum information, provide the first experimental demonstration that quantum states can be "probably approximately learned" with access to a number of copies of the state that scales linearly with the number of qubits, and pave the way to probing quantum states at new, larger scales.