Online Convex Optimisation: The Optimal Switching Regret for all Segmentations Simultaneously

We consider the classic problem of online convex optimisation. Whereas the notion of static regret is relevant for stationary problems, the notion of switching regret is more appropriate for non-stationary problems. A switching regret is defined relative to any segmentation of the trial sequence, and is equal to the sum of the static regrets of each segment. In this paper we show that, perhaps surprisingly, we can achieve the asymptotically optimal switching regret on every possible segmentation simultaneously. Our algorithm for doing so is very efficient: having a space and per-trial time complexity that is logarithmic in the time-horizon. Our algorithm also obtains novel bounds on its dynamic regret: being adaptive to variations in the rate of change of the comparator sequence.

Bandits with Abstention under Expert Advice

We study the classic problem of prediction with expert advice under bandit feedback. Our model assumes that one action, corresponding to the learner's abstention from play, has no reward or loss on every trial. We propose the CBA algorithm, which exploits this assumption to obtain reward bounds that can significantly improve those of the classical Exp4 algorithm. We can view our problem as the aggregation of confidence-rated predictors when the learner has the option of abstention from play. Importantly, we are the first to achieve bounds on the expected cumulative reward for general confidence-rated predictors. In the special case of specialists we achieve a novel reward bound, significantly improving previous bounds of SpecialistExp (treating abstention as another action). As an example application, we discuss learning unions of balls in a finite metric space. In this contextual setting, we devise an efficient implementation of CBA, reducing the runtime from quadratic to almost linear in the number of contexts. Preliminary experiments show that CBA improves over existing bandit algorithms.

Multi-class Graph Clustering via Approximated Effective $p$-Resistance

This paper develops an approximation to the (effective) $p$-resistance and applies it to multi-class clustering. Spectral methods based on the graph Laplacian and its generalization to the graph $p$-Laplacian have been a backbone of non-euclidean clustering techniques. The advantage of the $p$-Laplacian is that the parameter $p$ induces a controllable bias on cluster structure. The drawback of $p$-Laplacian eigenvector based methods is that the third and higher eigenvectors are difficult to compute. Thus, instead, we are motivated to use the $p$-resistance induced by the $p$-Laplacian for clustering. For $p$-resistance, small $p$ biases towards clusters with high internal connectivity while large $p$ biases towards clusters of small ``extent,'' that is a preference for smaller shortest-path distances between vertices in the cluster. However, the $p$-resistance is expensive to compute. We overcome this by developing an approximation to the $p$-resistance. We prove upper and lower bounds on this approximation and observe that it is exact when the graph is a tree. We also provide theoretical justification for the use of $p$-resistance for clustering. Finally, we provide experiments comparing our approximated $p$-resistance clustering to other $p$-Laplacian based methods.

Regret Guarantees for Adversarial Online Collaborative Filtering

We investigate the problem of online collaborative filtering under no-repetition constraints, whereby users need to be served content in an online fashion and a given user cannot be recommended the same content item more than once. We design and analyze a fully adaptive algorithm that works under biclustering assumptions on the user-item preference matrix, and show that this algorithm exhibits an optimal regret guarantee, while being oblivious to any prior knowledge about the sequence of users, the universe of items, as well as the biclustering parameters of the preference matrix. We further propose a more robust version of the algorithm which addresses the scenario when the preference matrix is adversarially perturbed. We then give regret guarantees that scale with the amount by which the preference matrix is perturbed from a biclustered structure. To our knowledge, these are the first results on online collaborative filtering that hold at this level of generality and adaptivity under no-repetition constraints.

Improved Regret Bounds for Tracking Experts with Memory

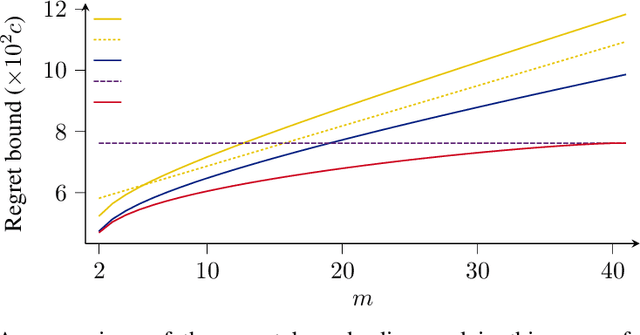
We address the problem of sequential prediction with expert advice in a non-stationary environment with long-term memory guarantees in the sense of Bousquet and Warmuth [4]. We give a linear-time algorithm that improves on the best known regret bounds [26]. This algorithm incorporates a relative entropy projection step. This projection is advantageous over previous weight-sharing approaches in that weight updates may come with implicit costs as in for example portfolio optimization. We give an algorithm to compute this projection step in linear time, which may be of independent interest.

Online Multitask Learning with Long-Term Memory

We introduce a novel online multitask setting. In this setting each task is partitioned into a sequence of segments that is unknown to the learner. Associated with each segment is a hypothesis from some hypothesis class. We give algorithms that are designed to exploit the scenario where there are many such segments but significantly fewer associated hypotheses. We prove regret bounds that hold for any segmentation of the tasks and any association of hypotheses to the segments. In the single-task setting this is equivalent to switching with long-term memory in the sense of [Bousquet and Warmuth; 2003]. We provide an algorithm that predicts on each trial in time linear in the number of hypotheses when the hypothesis class is finite. We also consider infinite hypothesis classes from reproducing kernel Hilbert spaces for which we give an algorithm whose per trial time complexity is cubic in the number of cumulative trials. In the single-task special case this is the first example of an efficient regret-bounded switching algorithm with long-term memory for a non-parametric hypothesis class.

Online Learning of Facility Locations

In this paper, we provide a rigorous theoretical investigation of an online learning version of the Facility Location problem which is motivated by emerging problems in real-world applications. In our formulation, we are given a set of sites and an online sequence of user requests. At each trial, the learner selects a subset of sites and then incurs a cost for each selected site and an additional cost which is the price of the user's connection to the nearest site in the selected subset. The problem may be solved by an application of the well-known Hedge algorithm. This would, however, require time and space exponential in the number of the given sites, which motivates our design of a novel quasi-linear time algorithm for this problem, with good theoretical guarantees on its performance.

Online Matrix Completion with Side Information

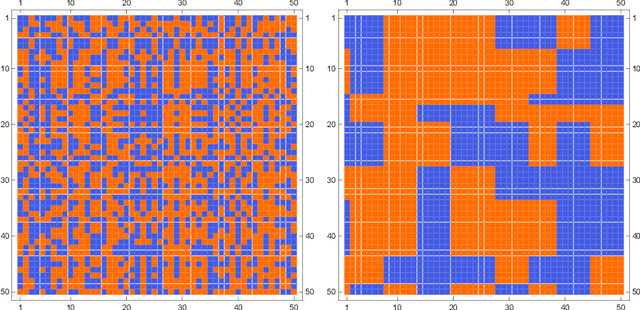
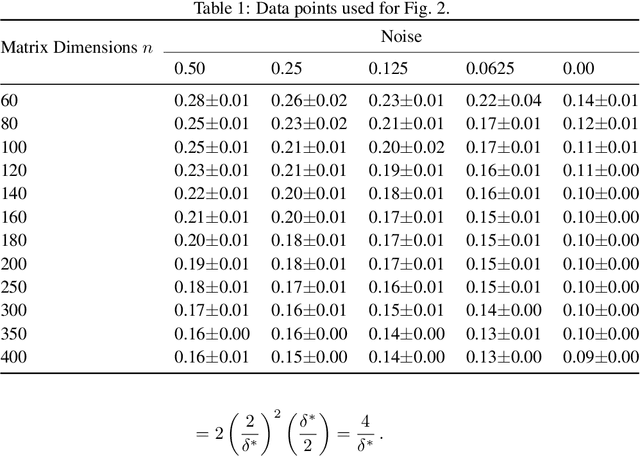
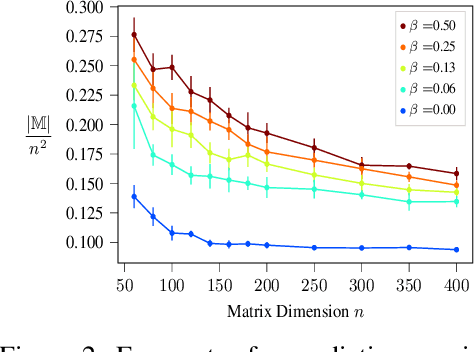
We give an online algorithm and prove novel mistake and regret bounds for online binary matrix completion with side information. The bounds we prove are of the form $\tilde{\mathcal{O}}({\mathcal{D}}/{\gamma^2})$. The term ${1}/{\gamma^2}$ is analogous to the usual margin term in SVM (perceptron) bounds. More specifically, if we assume that there is some factorization of the underlying $m\times n$ matrix into $\mathbf{P} \mathbf{Q}^{\top}$ where the rows of $\mathbf{P}$ are interpreted as ``classifiers'' in $\Re^d$ and the rows of $\mathbf{Q}$ as ``instances'' in $\Re^d$, then $\gamma$ is is the maximum (normalized) margin over all factorizations $\mathbf{P} \mathbf{Q}^{\top}$ consistent with the observed matrix. The quasi-dimension term $\mathcal{D}$ measures the quality of side information. In the presence of no side information, $\mathcal{D} = m+n$. However, if the side information is predictive of the underlying factorization of the matrix, then in the best case, $\mathcal{D} \in \mathcal{O}(k + \ell)$ where $k$ is the number of distinct row factors and $\ell$ is the number of distinct column factors. We additionally provide a generalization of our algorithm to the inductive setting. In this setting, the side information is not specified in advance. The results are similar to the transductive setting but in the best case, the quasi-dimension $\mathcal{D}$ is now bounded by $\mathcal{O}(k^2 + \ell^2)$.

Predicting Switching Graph Labelings with Cluster Specialists

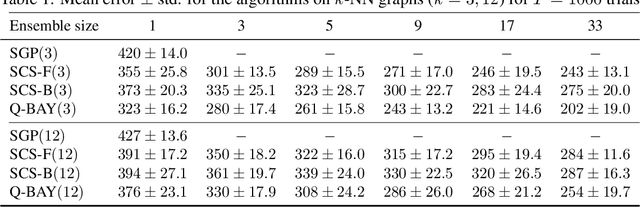
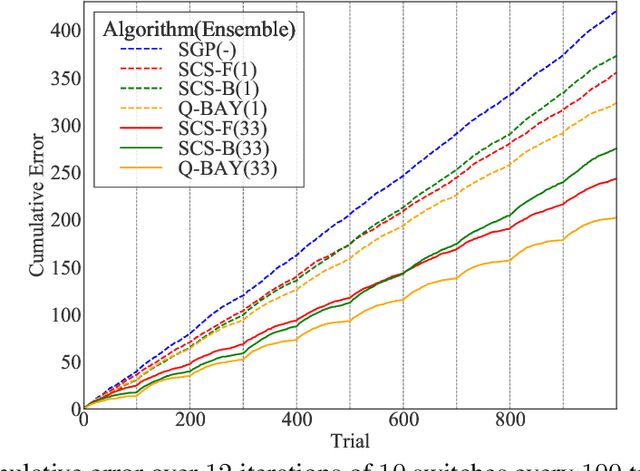
We address the problem of predicting the labeling of a graph in an online setting when the labeling is changing over time. We provide three mistake-bounded algorithms based on three paradigmatic methods for online algorithm design. The algorithm with the strongest guarantee is a quasi-Bayesian classifier which requires $\mathcal{O}(t \log n)$ time to predict at trial $t$ on an $n$-vertex graph. The fastest algorithm (with the weakest guarantee) is based on a specialist [10] approach and surprisingly only requires $\mathcal{O}(\log n)$ time on any trial $t$. We also give an algorithm based on a kernelized Perceptron with an intermediate per-trial time complexity of $\mathcal{O}(n)$ and a mistake bound which is not strictly comparable. Finally, we provide experiments on simulated data comparing these methods.

Quantum machine learning: a classical perspective

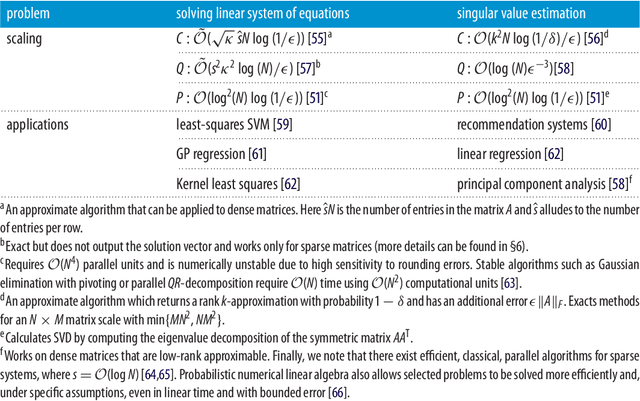
Recently, increased computational power and data availability, as well as algorithmic advances, have led machine learning techniques to impressive results in regression, classification, data-generation and reinforcement learning tasks. Despite these successes, the proximity to the physical limits of chip fabrication alongside the increasing size of datasets are motivating a growing number of researchers to explore the possibility of harnessing the power of quantum computation to speed-up classical machine learning algorithms. Here we review the literature in quantum machine learning and discuss perspectives for a mixed readership of classical machine learning and quantum computation experts. Particular emphasis will be placed on clarifying the limitations of quantum algorithms, how they compare with their best classical counterparts and why quantum resources are expected to provide advantages for learning problems. Learning in the presence of noise and certain computationally hard problems in machine learning are identified as promising directions for the field. Practical questions, like how to upload classical data into quantum form, will also be addressed.