Empathy and the Right to Be an Exception: What LLMs Can and Cannot Do

Advances in the performance of large language models (LLMs) have led some researchers to propose the emergence of theory of mind (ToM) in artificial intelligence (AI). LLMs can attribute beliefs, desires, intentions, and emotions, and they will improve in their accuracy. Rather than employing the characteristically human method of empathy, they learn to attribute mental states by recognizing linguistic patterns in a dataset that typically do not include that individual. We ask whether LLMs' inability to empathize precludes them from honoring an individual's right to be an exception, that is, from making assessments of character and predictions of behavior that reflect appropriate sensitivity to a person's individuality. Can LLMs seriously consider an individual's claim that their case is different based on internal mental states like beliefs, desires, and intentions, or are they limited to judging that case based on its similarities to others? We propose that the method of empathy has special significance for honoring the right to be an exception that is distinct from the value of predictive accuracy, at which LLMs excel. We conclude by considering whether using empathy to consider exceptional cases has intrinsic or merely practical value and we introduce conceptual and empirical avenues for advancing this investigation.

Decolonial AI Alignment: Viśesadharma, Argument, and Artistic Expression

Prior work has explicated the coloniality of artificial intelligence (AI) development and deployment. One process that that work has not engaged with much is alignment: the tuning of large language model (LLM) behavior to be in line with desired values based on fine-grained human feedback. In addition to other practices, colonialism has a history of altering the beliefs and values of colonized peoples; this history is recapitulated in current LLM alignment practices. We suggest that AI alignment be decolonialized using three proposals: (a) changing the base moral philosophy from Western philosophy to dharma, (b) permitting traditions of argument and pluralism in alignment technologies, and (c) expanding the epistemology of values beyond instructions or commandments given in natural language.

Keeping Up with the Language Models: Robustness-Bias Interplay in NLI Data and Models

Auditing unwanted social bias in language models (LMs) is inherently hard due to the multidisciplinary nature of the work. In addition, the rapid evolution of LMs can make benchmarks irrelevant in no time. Bias auditing is further complicated by LM brittleness: when a presumably biased outcome is observed, is it due to model bias or model brittleness? We propose enlisting the models themselves to help construct bias auditing datasets that remain challenging, and introduce bias measures that distinguish between types of model errors. First, we extend an existing bias benchmark for NLI (BBNLI) using a combination of LM-generated lexical variations, adversarial filtering, and human validation. We demonstrate that the newly created dataset (BBNLInext) is more challenging than BBNLI: on average, BBNLI-next reduces the accuracy of state-of-the-art NLI models from 95.3%, as observed by BBNLI, to 58.6%. Second, we employ BBNLI-next to showcase the interplay between robustness and bias, and the subtlety in differentiating between the two. Third, we point out shortcomings in current bias scores used in the literature and propose bias measures that take into account pro-/anti-stereotype bias and model brittleness. We will publicly release the BBNLI-next dataset to inspire research on rapidly expanding benchmarks to keep up with model evolution, along with research on the robustness-bias interplay in bias auditing. Note: This paper contains offensive text examples.

Towards Healthy AI: Large Language Models Need Therapists Too

Recent advances in large language models (LLMs) have led to the development of powerful AI chatbots capable of engaging in natural and human-like conversations. However, these chatbots can be potentially harmful, exhibiting manipulative, gaslighting, and narcissistic behaviors. We define Healthy AI to be safe, trustworthy and ethical. To create healthy AI systems, we present the SafeguardGPT framework that uses psychotherapy to correct for these harmful behaviors in AI chatbots. The framework involves four types of AI agents: a Chatbot, a "User," a "Therapist," and a "Critic." We demonstrate the effectiveness of SafeguardGPT through a working example of simulating a social conversation. Our results show that the framework can improve the quality of conversations between AI chatbots and humans. Although there are still several challenges and directions to be addressed in the future, SafeguardGPT provides a promising approach to improving the alignment between AI chatbots and human values. By incorporating psychotherapy and reinforcement learning techniques, the framework enables AI chatbots to learn and adapt to human preferences and values in a safe and ethical way, contributing to the development of a more human-centric and responsible AI.

Function Composition in Trustworthy Machine Learning: Implementation Choices, Insights, and Questions

Ensuring trustworthiness in machine learning (ML) models is a multi-dimensional task. In addition to the traditional notion of predictive performance, other notions such as privacy, fairness, robustness to distribution shift, adversarial robustness, interpretability, explainability, and uncertainty quantification are important considerations to evaluate and improve (if deficient). However, these sub-disciplines or 'pillars' of trustworthiness have largely developed independently, which has limited us from understanding their interactions in real-world ML pipelines. In this paper, focusing specifically on compositions of functions arising from the different pillars, we aim to reduce this gap, develop new insights for trustworthy ML, and answer questions such as the following. Does the composition of multiple fairness interventions result in a fairer model compared to a single intervention? How do bias mitigation algorithms for fairness affect local post-hoc explanations? Does a defense algorithm for untargeted adversarial attacks continue to be effective when composed with a privacy transformation? Toward this end, we report initial empirical results and new insights from 9 different compositions of functions (or pipelines) on 7 real-world datasets along two trustworthy dimensions - fairness and explainability. We also report progress, and implementation choices, on an extensible composer tool to encourage the combination of functionalities from multiple pillars. To-date, the tool supports bias mitigation algorithms for fairness and post-hoc explainability methods. We hope this line of work encourages the thoughtful consideration of multiple pillars when attempting to formulate and resolve a trustworthiness problem.

Fair Infinitesimal Jackknife: Mitigating the Influence of Biased Training Data Points Without Refitting

In consequential decision-making applications, mitigating unwanted biases in machine learning models that yield systematic disadvantage to members of groups delineated by sensitive attributes such as race and gender is one key intervention to strive for equity. Focusing on demographic parity and equality of opportunity, in this paper we propose an algorithm that improves the fairness of a pre-trained classifier by simply dropping carefully selected training data points. We select instances based on their influence on the fairness metric of interest, computed using an infinitesimal jackknife-based approach. The dropping of training points is done in principle, but in practice does not require the model to be refit. Crucially, we find that such an intervention does not substantially reduce the predictive performance of the model but drastically improves the fairness metric. Through careful experiments, we evaluate the effectiveness of the proposed approach on diverse tasks and find that it consistently improves upon existing alternatives.

On the Safety of Interpretable Machine Learning: A Maximum Deviation Approach

Interpretable and explainable machine learning has seen a recent surge of interest. We focus on safety as a key motivation behind the surge and make the relationship between interpretability and safety more quantitative. Toward assessing safety, we introduce the concept of maximum deviation via an optimization problem to find the largest deviation of a supervised learning model from a reference model regarded as safe. We then show how interpretability facilitates this safety assessment. For models including decision trees, generalized linear and additive models, the maximum deviation can be computed exactly and efficiently. For tree ensembles, which are not regarded as interpretable, discrete optimization techniques can still provide informative bounds. For a broader class of piecewise Lipschitz functions, we leverage the multi-armed bandit literature to show that interpretability produces tighter (regret) bounds on the maximum deviation. We present case studies, including one on mortgage approval, to illustrate our methods and the insights about models that may be obtained from deviation maximization.

Equi-Tuning: Group Equivariant Fine-Tuning of Pretrained Models

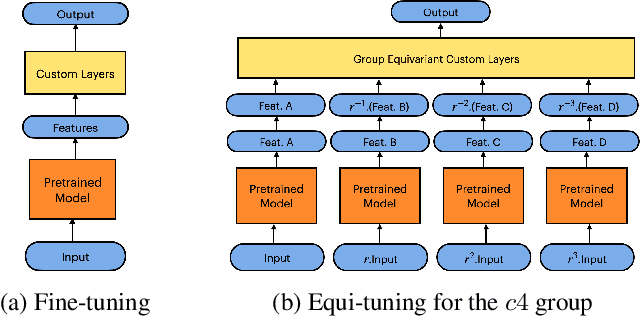
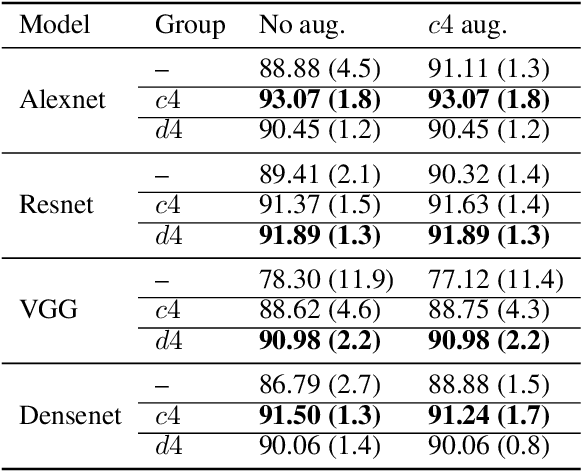
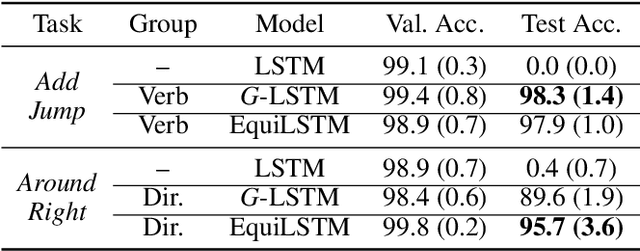
We introduce equi-tuning, a novel fine-tuning method that transforms (potentially non-equivariant) pretrained models into group equivariant models while incurring minimum $L_2$ loss between the feature representations of the pretrained and the equivariant models. Large pretrained models can be equi-tuned for different groups to satisfy the needs of various downstream tasks. Equi-tuned models benefit from both group equivariance as an inductive bias and semantic priors from pretrained models. We provide applications of equi-tuning on three different tasks: image classification, compositional generalization in language, and fairness in natural language generation (NLG). We also provide a novel group-theoretic definition for fairness in NLG. The effectiveness of this definition is shown by testing it against a standard empirical method of fairness in NLG. We provide experimental results for equi-tuning using a variety of pretrained models: Alexnet, Resnet, VGG, and Densenet for image classification; RNNs, GRUs, and LSTMs for compositional generalization; and GPT2 for fairness in NLG. We test these models on benchmark datasets across all considered tasks to show the generality and effectiveness of the proposed method.

Minimax AUC Fairness: Efficient Algorithm with Provable Convergence

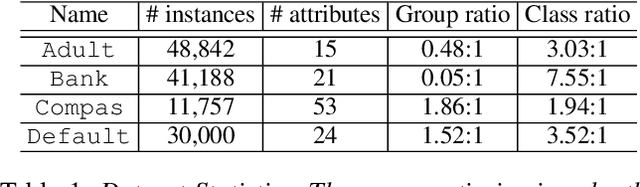
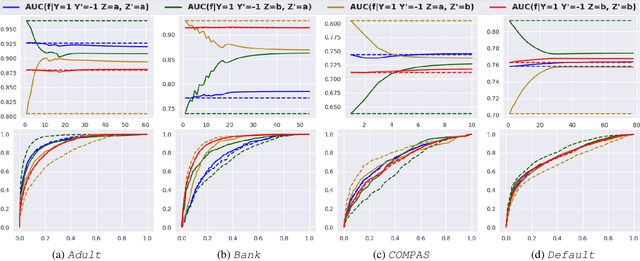
The use of machine learning models in consequential decision making often exacerbates societal inequity, in particular yielding disparate impact on members of marginalized groups defined by race and gender. The area under the ROC curve (AUC) is widely used to evaluate the performance of a scoring function in machine learning, but is studied in algorithmic fairness less than other performance metrics. Due to the pairwise nature of the AUC, defining an AUC-based group fairness metric is pairwise-dependent and may involve both \emph{intra-group} and \emph{inter-group} AUCs. Importantly, considering only one category of AUCs is not sufficient to mitigate unfairness in AUC optimization. In this paper, we propose a minimax learning and bias mitigation framework that incorporates both intra-group and inter-group AUCs while maintaining utility. Based on this Rawlsian framework, we design an efficient stochastic optimization algorithm and prove its convergence to the minimum group-level AUC. We conduct numerical experiments on both synthetic and real-world datasets to validate the effectiveness of the minimax framework and the proposed optimization algorithm.

Differentially Private SGDA for Minimax Problems

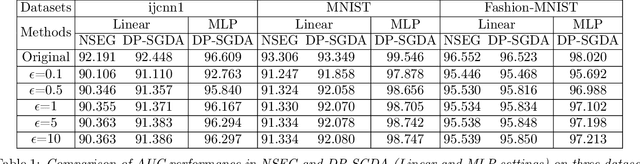
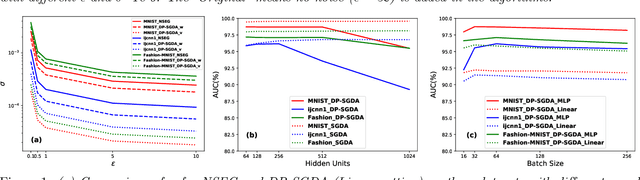
Stochastic gradient descent ascent (SGDA) and its variants have been the workhorse for solving minimax problems. However, in contrast to the well-studied stochastic gradient descent (SGD) with differential privacy (DP) constraints, there is little work on understanding the generalization (utility) of SGDA with DP constraints. In this paper, we use the algorithmic stability approach to establish the generalization (utility) of DP-SGDA in different settings. In particular, for the convex-concave setting, we prove that the DP-SGDA can achieve an optimal utility rate in terms of the weak primal-dual population risk in both smooth and non-smooth cases. To our best knowledge, this is the first-ever-known result for DP-SGDA in the non-smooth case. We further provide its utility analysis in the nonconvex-strongly-concave setting which is the first-ever-known result in terms of the primal population risk. The convergence and generalization results for this nonconvex setting are new even in the non-private setting. Finally, numerical experiments are conducted to demonstrate the effectiveness of DP-SGDA for both convex and nonconvex cases.