Slicing Mutual Information Generalization Bounds for Neural Networks

The ability of machine learning (ML) algorithms to generalize well to unseen data has been studied through the lens of information theory, by bounding the generalization error with the input-output mutual information (MI), i.e., the MI between the training data and the learned hypothesis. Yet, these bounds have limited practicality for modern ML applications (e.g., deep learning), due to the difficulty of evaluating MI in high dimensions. Motivated by recent findings on the compressibility of neural networks, we consider algorithms that operate by slicing the parameter space, i.e., trained on random lower-dimensional subspaces. We introduce new, tighter information-theoretic generalization bounds tailored for such algorithms, demonstrating that slicing improves generalization. Our bounds offer significant computational and statistical advantages over standard MI bounds, as they rely on scalable alternative measures of dependence, i.e., disintegrated mutual information and $k$-sliced mutual information. Then, we extend our analysis to algorithms whose parameters do not need to exactly lie on random subspaces, by leveraging rate-distortion theory. This strategy yields generalization bounds that incorporate a distortion term measuring model compressibility under slicing, thereby tightening existing bounds without compromising performance or requiring model compression. Building on this, we propose a regularization scheme enabling practitioners to control generalization through compressibility. Finally, we empirically validate our results and achieve the computation of non-vacuous information-theoretic generalization bounds for neural networks, a task that was previously out of reach.

Asymmetry in Low-Rank Adapters of Foundation Models

Parameter-efficient fine-tuning optimizes large, pre-trained foundation models by updating a subset of parameters; in this class, Low-Rank Adaptation (LoRA) is particularly effective. Inspired by an effort to investigate the different roles of LoRA matrices during fine-tuning, this paper characterizes and leverages unexpected asymmetry in the importance of low-rank adapter matrices. Specifically, when updating the parameter matrices of a neural network by adding a product $BA$, we observe that the $B$ and $A$ matrices have distinct functions: $A$ extracts features from the input, while $B$ uses these features to create the desired output. Based on this observation, we demonstrate that fine-tuning $B$ is inherently more effective than fine-tuning $A$, and that a random untrained $A$ should perform nearly as well as a fine-tuned one. Using an information-theoretic lens, we also bound the generalization of low-rank adapters, showing that the parameter savings of exclusively training $B$ improves the bound. We support our conclusions with experiments on RoBERTa, BART-Large, LLaMA-2, and ViTs.

Federated Wasserstein Distance

We introduce a principled way of computing the Wasserstein distance between two distributions in a federated manner. Namely, we show how to estimate the Wasserstein distance between two samples stored and kept on different devices/clients whilst a central entity/server orchestrates the computations (again, without having access to the samples). To achieve this feat, we take advantage of the geometric properties of the Wasserstein distance -- in particular, the triangle inequality -- and that of the associated {\em geodesics}: our algorithm, FedWad (for Federated Wasserstein Distance), iteratively approximates the Wasserstein distance by manipulating and exchanging distributions from the space of geodesics in lieu of the input samples. In addition to establishing the convergence properties of FedWad, we provide empirical results on federated coresets and federate optimal transport dataset distance, that we respectively exploit for building a novel federated model and for boosting performance of popular federated learning algorithms.

Unbalanced Optimal Transport meets Sliced-Wasserstein

Optimal transport (OT) has emerged as a powerful framework to compare probability measures, a fundamental task in many statistical and machine learning problems. Substantial advances have been made over the last decade in designing OT variants which are either computationally and statistically more efficient, or more robust to the measures and datasets to compare. Among them, sliced OT distances have been extensively used to mitigate optimal transport's cubic algorithmic complexity and curse of dimensionality. In parallel, unbalanced OT was designed to allow comparisons of more general positive measures, while being more robust to outliers. In this paper, we propose to combine these two concepts, namely slicing and unbalanced OT, to develop a general framework for efficiently comparing positive measures. We propose two new loss functions based on the idea of slicing unbalanced OT, and study their induced topology and statistical properties. We then develop a fast Frank-Wolfe-type algorithm to compute these loss functions, and show that the resulting methodology is modular as it encompasses and extends prior related work. We finally conduct an empirical analysis of our loss functions and methodology on both synthetic and real datasets, to illustrate their relevance and applicability.

Shedding a PAC-Bayesian Light on Adaptive Sliced-Wasserstein Distances

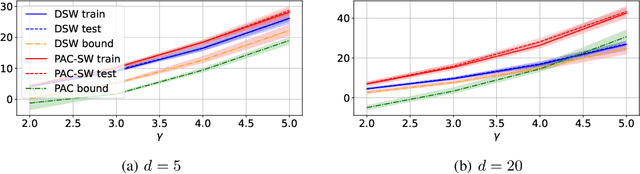
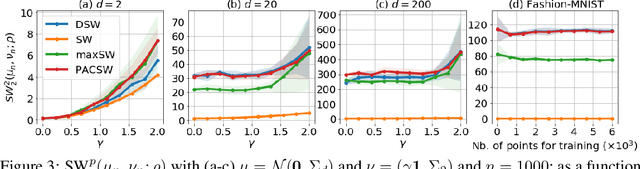
The Sliced-Wasserstein distance (SW) is a computationally efficient and theoretically grounded alternative to the Wasserstein distance. Yet, the literature on its statistical properties with respect to the distribution of slices, beyond the uniform measure, is scarce. To bring new contributions to this line of research, we leverage the PAC-Bayesian theory and the central observation that SW actually hinges on a slice-distribution-dependent Gibbs risk, the kind of quantity PAC-Bayesian bounds have been designed to characterize. We provide four types of results: i) PAC-Bayesian generalization bounds that hold on what we refer as adaptive Sliced-Wasserstein distances, i.e. distances defined with respect to any distribution of slices, ii) a procedure to learn the distribution of slices that yields a maximally discriminative SW, by optimizing our PAC-Bayesian bounds, iii) an insight on how the performance of the so-called distributional Sliced-Wasserstein distance may be explained through our theory, and iv) empirical illustrations of our findings.

Fast Approximation of the Sliced-Wasserstein Distance Using Concentration of Random Projections

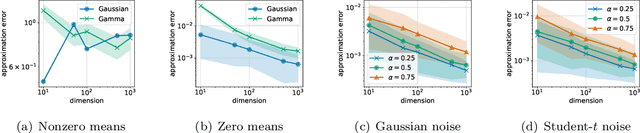
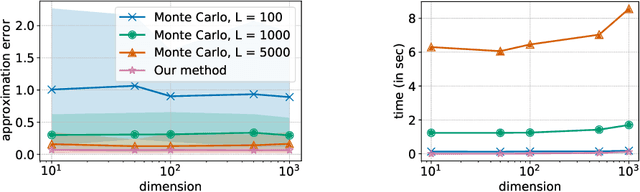
The Sliced-Wasserstein distance (SW) is being increasingly used in machine learning applications as an alternative to the Wasserstein distance and offers significant computational and statistical benefits. Since it is defined as an expectation over random projections, SW is commonly approximated by Monte Carlo. We adopt a new perspective to approximate SW by making use of the concentration of measure phenomenon: under mild assumptions, one-dimensional projections of a high-dimensional random vector are approximately Gaussian. Based on this observation, we develop a simple deterministic approximation for SW. Our method does not require sampling a number of random projections, and is therefore both accurate and easy to use compared to the usual Monte Carlo approximation. We derive nonasymptotical guarantees for our approach, and show that the approximation error goes to zero as the dimension increases, under a weak dependence condition on the data distribution. We validate our theoretical findings on synthetic datasets, and illustrate the proposed approximation on a generative modeling problem.

Statistical and Topological Properties of Sliced Probability Divergences

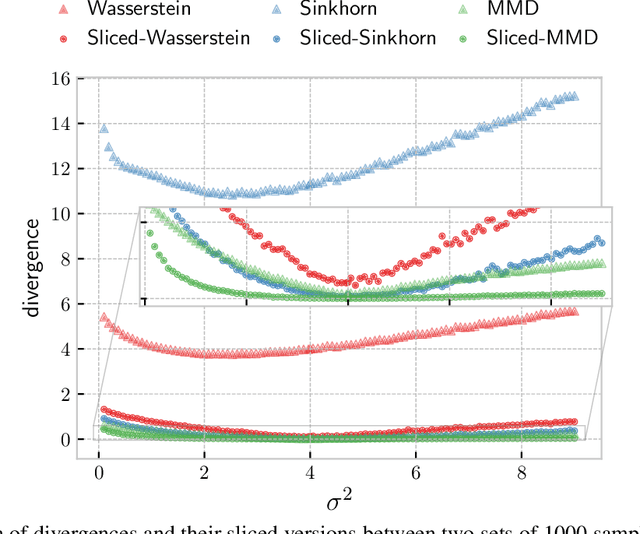
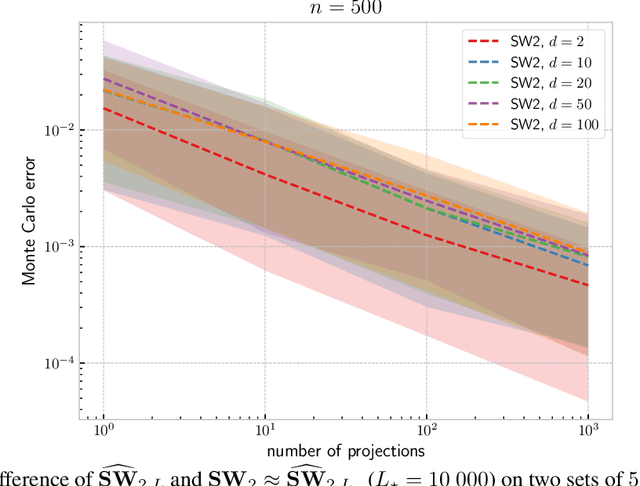
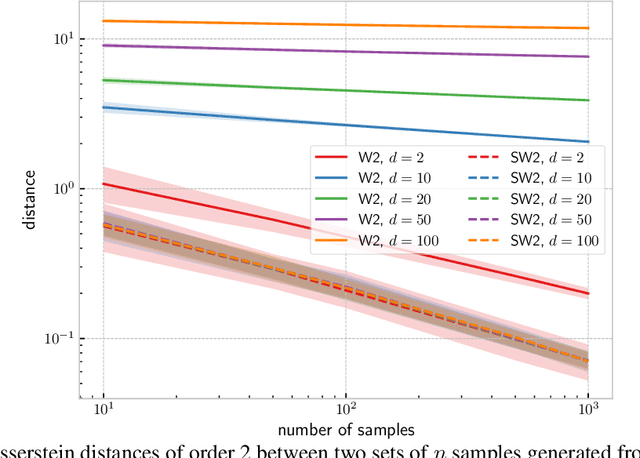
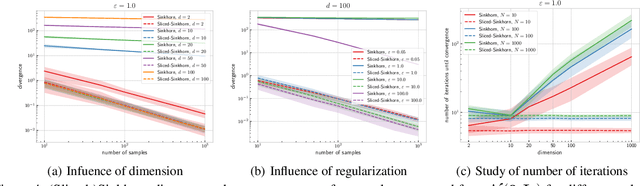
The idea of slicing divergences has been proven to be successful when comparing two probability measures in various machine learning applications including generative modeling, and consists in computing the expected value of a `base divergence' between one-dimensional random projections of the two measures. However, the computational and statistical consequences of such a technique have not yet been well-established. In this paper, we aim at bridging this gap and derive some properties of sliced divergence functions. First, we show that slicing preserves the metric axioms and the weak continuity of the divergence, implying that the sliced divergence will share similar topological properties. We then precise the results in the case where the base divergence belongs to the class of integral probability metrics. On the other hand, we establish that, under mild conditions, the sample complexity of the sliced divergence does not depend on the dimension, even when the base divergence suffers from the curse of dimensionality. We finally apply our general results to the Wasserstein distance and Sinkhorn divergences, and illustrate our theory on both synthetic and real data experiments.

Generalized Sliced Distances for Probability Distributions

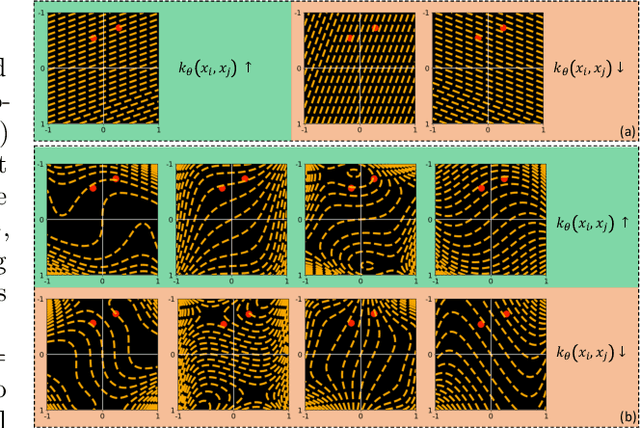
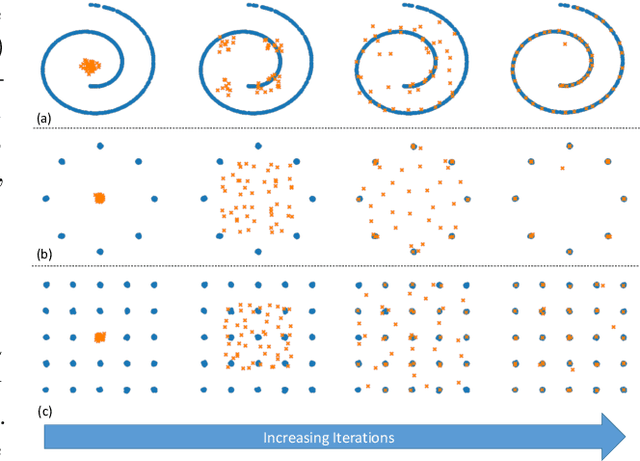
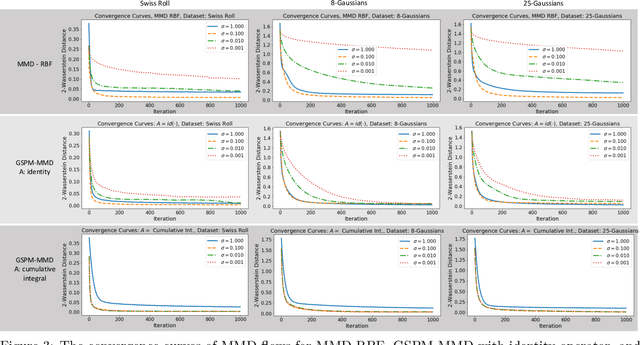
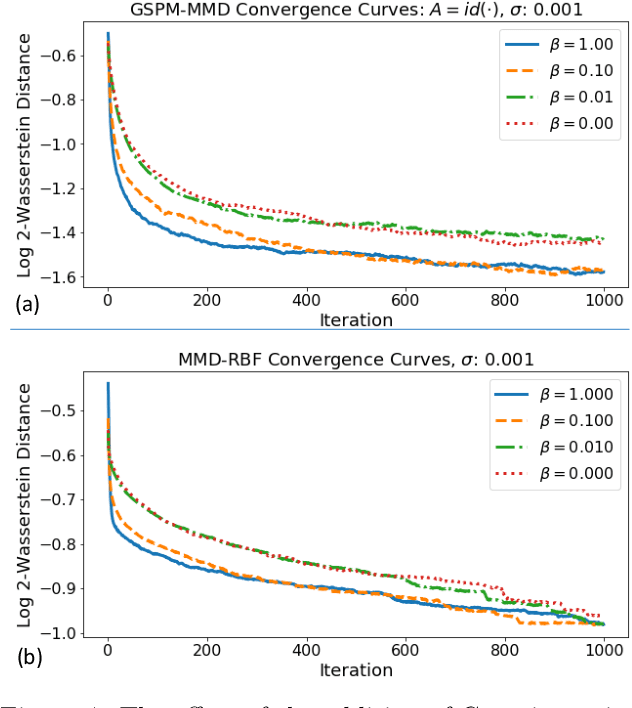
Probability metrics have become an indispensable part of modern statistics and machine learning, and they play a quintessential role in various applications, including statistical hypothesis testing and generative modeling. However, in a practical setting, the convergence behavior of the algorithms built upon these distances have not been well established, except for a few specific cases. In this paper, we introduce a broad family of probability metrics, coined as Generalized Sliced Probability Metrics (GSPMs), that are deeply rooted in the generalized Radon transform. We first verify that GSPMs are metrics. Then, we identify a subset of GSPMs that are equivalent to maximum mean discrepancy (MMD) with novel positive definite kernels, which come with a unique geometric interpretation. Finally, by exploiting this connection, we consider GSPM-based gradient flows for generative modeling applications and show that under mild assumptions, the gradient flow converges to the global optimum. We illustrate the utility of our approach on both real and synthetic problems.

Approximate Bayesian Computation with the Sliced-Wasserstein Distance

Approximate Bayesian Computation (ABC) is a popular method for approximate inference in generative models with intractable but easy-to-sample likelihood. It constructs an approximate posterior distribution by finding parameters for which the simulated data are close to the observations in terms of summary statistics. These statistics are defined beforehand and might induce a loss of information, which has been shown to deteriorate the quality of the approximation. To overcome this problem, Wasserstein-ABC has been recently proposed, and compares the datasets via the Wasserstein distance between their empirical distributions, but does not scale well to the dimension or the number of samples. We propose a new ABC technique, called Sliced-Wasserstein ABC and based on the Sliced-Wasserstein distance, which has better computational and statistical properties. We derive two theoretical results showing the asymptotical consistency of our approach, and we illustrate its advantages on synthetic data and an image denoising task.

Safe Policy Improvement with Soft Baseline Bootstrapping

Batch Reinforcement Learning (Batch RL) consists in training a policy using trajectories collected with another policy, called the behavioural policy. Safe policy improvement (SPI) provides guarantees with high probability that the trained policy performs better than the behavioural policy, also called baseline in this setting. Previous work shows that the SPI objective improves mean performance as compared to using the basic RL objective, which boils down to solving the MDP with maximum likelihood. Here, we build on that work and improve more precisely the SPI with Baseline Bootstrapping algorithm (SPIBB) by allowing the policy search over a wider set of policies. Instead of binarily classifying the state-action pairs into two sets (the \textit{uncertain} and the \textit{safe-to-train-on} ones), we adopt a softer strategy that controls the error in the value estimates by constraining the policy change according to the local model uncertainty. The method can take more risks on uncertain actions all the while remaining provably-safe, and is therefore less conservative than the state-of-the-art methods. We propose two algorithms (one optimal and one approximate) to solve this constrained optimization problem and empirically show a significant improvement over existing SPI algorithms both on finite MDPs and on infinite MDPs with a neural network function approximation.