Thibault Séjourné
Unbalanced Optimal Transport meets Sliced-Wasserstein
Jun 12, 2023Abstract:Optimal transport (OT) has emerged as a powerful framework to compare probability measures, a fundamental task in many statistical and machine learning problems. Substantial advances have been made over the last decade in designing OT variants which are either computationally and statistically more efficient, or more robust to the measures and datasets to compare. Among them, sliced OT distances have been extensively used to mitigate optimal transport's cubic algorithmic complexity and curse of dimensionality. In parallel, unbalanced OT was designed to allow comparisons of more general positive measures, while being more robust to outliers. In this paper, we propose to combine these two concepts, namely slicing and unbalanced OT, to develop a general framework for efficiently comparing positive measures. We propose two new loss functions based on the idea of slicing unbalanced OT, and study their induced topology and statistical properties. We then develop a fast Frank-Wolfe-type algorithm to compute these loss functions, and show that the resulting methodology is modular as it encompasses and extends prior related work. We finally conduct an empirical analysis of our loss functions and methodology on both synthetic and real datasets, to illustrate their relevance and applicability.
Unbalanced Optimal Transport, from Theory to Numerics
Nov 16, 2022Abstract:Optimal Transport (OT) has recently emerged as a central tool in data sciences to compare in a geometrically faithful way point clouds and more generally probability distributions. The wide adoption of OT into existing data analysis and machine learning pipelines is however plagued by several shortcomings. This includes its lack of robustness to outliers, its high computational costs, the need for a large number of samples in high dimension and the difficulty to handle data in distinct spaces. In this review, we detail several recently proposed approaches to mitigate these issues. We insist in particular on unbalanced OT, which compares arbitrary positive measures, not restricted to probability distributions (i.e. their total mass can vary). This generalization of OT makes it robust to outliers and missing data. The second workhorse of modern computational OT is entropic regularization, which leads to scalable algorithms while lowering the sample complexity in high dimension. The last point presented in this review is the Gromov-Wasserstein (GW) distance, which extends OT to cope with distributions belonging to different metric spaces. The main motivation for this review is to explain how unbalanced OT, entropic regularization and GW can work hand-in-hand to turn OT into efficient geometric loss functions for data sciences.
Faster Unbalanced Optimal Transport: Translation invariant Sinkhorn and 1-D Frank-Wolfe
Jan 03, 2022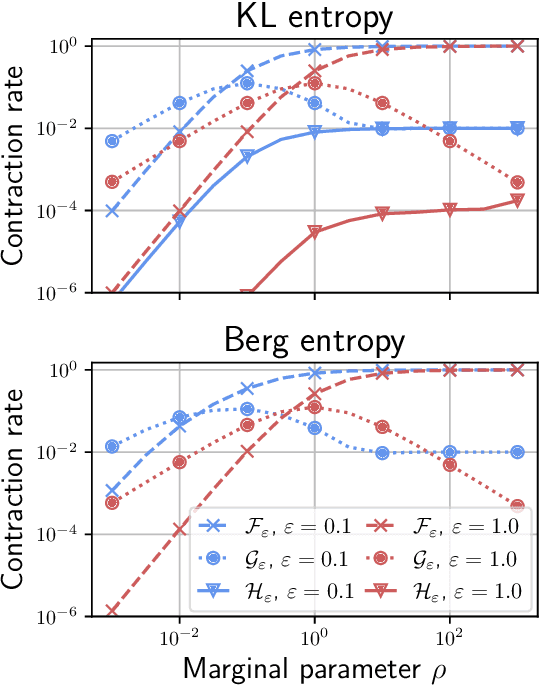
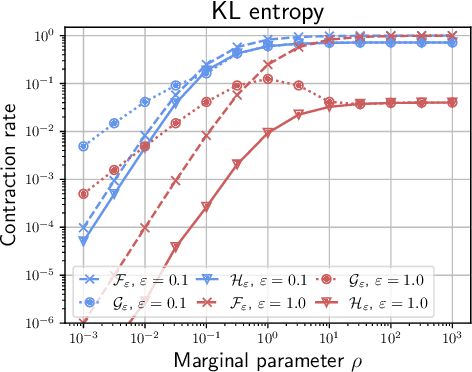

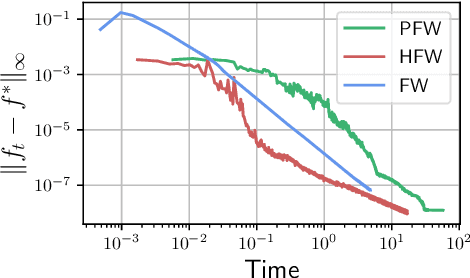
Abstract:Unbalanced optimal transport (UOT) extends optimal transport (OT) to take into account mass variations to compare distributions. This is crucial to make OT successful in ML applications, making it robust to data normalization and outliers. The baseline algorithm is Sinkhorn, but its convergence speed might be significantly slower for UOT than for OT. In this work, we identify the cause for this deficiency, namely the lack of a global normalization of the iterates, which equivalently corresponds to a translation of the dual OT potentials. Our first contribution leverages this idea to develop a provably accelerated Sinkhorn algorithm (coined 'translation invariant Sinkhorn') for UOT, bridging the computational gap with OT. Our second contribution focusses on 1-D UOT and proposes a Frank-Wolfe solver applied to this translation invariant formulation. The linear oracle of each steps amounts to solving a 1-D OT problems, resulting in a linear time complexity per iteration. Our last contribution extends this method to the computation of UOT barycenter of 1-D measures. Numerical simulations showcase the convergence speed improvement brought by these three approaches.
Unbalanced minibatch Optimal Transport; applications to Domain Adaptation
Mar 05, 2021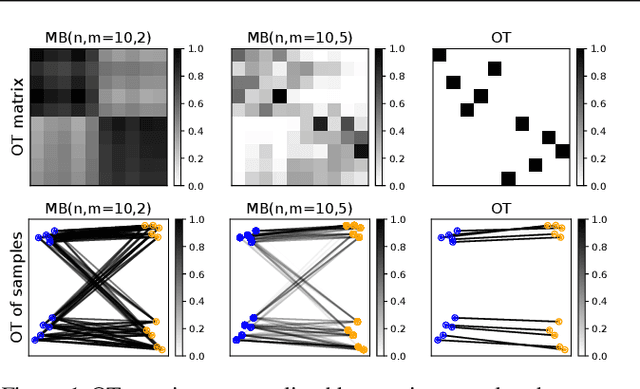
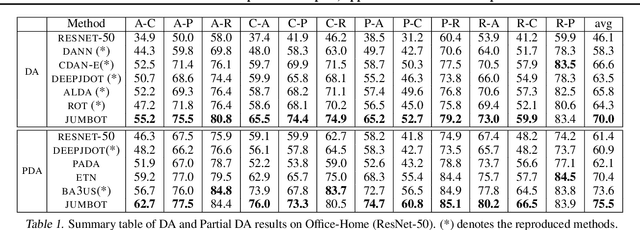

Abstract:Optimal transport distances have found many applications in machine learning for their capacity to compare non-parametric probability distributions. Yet their algorithmic complexity generally prevents their direct use on large scale datasets. Among the possible strategies to alleviate this issue, practitioners can rely on computing estimates of these distances over subsets of data, {\em i.e.} minibatches. While computationally appealing, we highlight in this paper some limits of this strategy, arguing it can lead to undesirable smoothing effects. As an alternative, we suggest that the same minibatch strategy coupled with unbalanced optimal transport can yield more robust behavior. We discuss the associated theoretical properties, such as unbiased estimators, existence of gradients and concentration bounds. Our experimental study shows that in challenging problems associated to domain adaptation, the use of unbalanced optimal transport leads to significantly better results, competing with or surpassing recent baselines.
The Unbalanced Gromov Wasserstein Distance: Conic Formulation and Relaxation
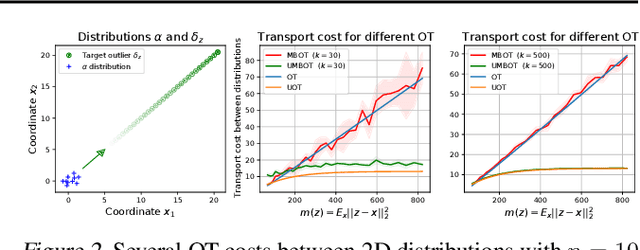
Sep 09, 2020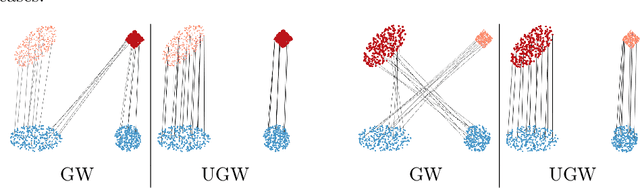
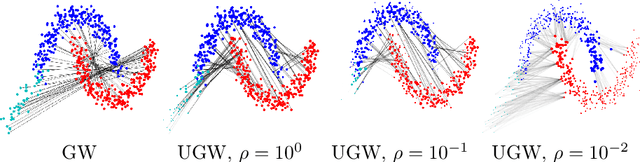
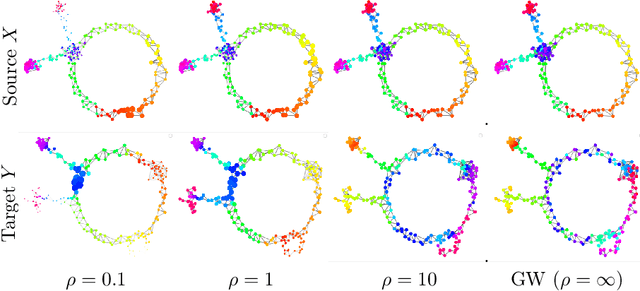
Abstract:Comparing metric measure spaces (i.e. a metric space endowed with a probability distribution) is at the heart of many machine learning problems. This includes for instance predicting properties of molecules in quantum chemistry or generating graphs with varying connectivity. The most popular distance between such metric measure spaces is the Gromov-Wasserstein (GW) distance, which is the solution of a quadratic assignment problem. This distance has been successfully applied to supervised learning and generative modeling, for applications as diverse as quantum chemistry or natural language processing. The GW distance is however limited to the comparison of metric measure spaces endowed with a \emph{probability} distribution. This strong limitation is problematic for many applications in ML where there is no a priori natural normalization on the total mass of the data. Furthermore, imposing an exact conservation of mass across spaces is not robust to outliers and often leads to irregular matching. To alleviate these issues, we introduce two Unbalanced Gromov-Wasserstein formulations: a distance and a more computationally tractable upper-bounding relaxation. They both allow the comparison of metric spaces equipped with arbitrary positive measures up to isometries.
Sinkhorn Divergences for Unbalanced Optimal Transport
Oct 28, 2019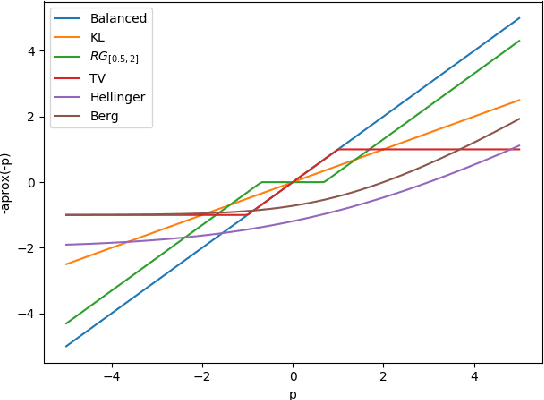
Abstract:This paper extends the formulation of Sinkhorn divergences to the unbalanced setting of arbitrary positive measures, providing both theoretical and algorithmic advances. Sinkhorn divergences leverage the entropic regularization of Optimal Transport (OT) to define geometric loss functions. They are differentiable, cheap to compute and do not suffer from the curse of dimensionality, while maintaining the geometric properties of OT, in particular they metrize the weak$^*$ convergence. Extending these divergences to the unbalanced setting is of utmost importance since most applications in data sciences require to handle both transportation and creation/destruction of mass. This includes for instance problems as diverse as shape registration in medical imaging, density fitting in statistics, generative modeling in machine learning, and particles flows involving birth/death dynamics. Our first set of contributions is the definition and the theoretical analysis of the unbalanced Sinkhorn divergences. They enjoy the same properties as the balanced divergences (classical OT), which are obtained as a special case. Indeed, we show that they are convex, differentiable and metrize the weak$^*$ convergence. Our second set of contributions studies generalized Sinkkhorn iterations, which enable a fast, stable and massively parallelizable algorithm to compute these divergences. We show, under mild assumptions, a linear rate of convergence, independent of the number of samples, i.e. which can cope with arbitrary input measures. We also highlight the versatility of this method, which takes benefit from the latest advances in term of GPU computing, for instance through the KeOps library for fast and scalable kernel operations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge