Attention-based clustering

Transformers have emerged as a powerful neural network architecture capable of tackling a wide range of learning tasks. In this work, we provide a theoretical analysis of their ability to automatically extract structure from data in an unsupervised setting. In particular, we demonstrate their suitability for clustering when the input data is generated from a Gaussian mixture model. To this end, we study a simplified two-head attention layer and define a population risk whose minimization with unlabeled data drives the head parameters to align with the true mixture centroids.

Taking a Big Step: Large Learning Rates in Denoising Score Matching Prevent Memorization

Denoising score matching plays a pivotal role in the performance of diffusion-based generative models. However, the empirical optimal score--the exact solution to the denoising score matching--leads to memorization, where generated samples replicate the training data. Yet, in practice, only a moderate degree of memorization is observed, even without explicit regularization. In this paper, we investigate this phenomenon by uncovering an implicit regularization mechanism driven by large learning rates. Specifically, we show that in the small-noise regime, the empirical optimal score exhibits high irregularity. We then prove that, when trained by stochastic gradient descent with a large enough learning rate, neural networks cannot stably converge to a local minimum with arbitrarily small excess risk. Consequently, the learned score cannot be arbitrarily close to the empirical optimal score, thereby mitigating memorization. To make the analysis tractable, we consider one-dimensional data and two-layer neural networks. Experiments validate the crucial role of the learning rate in preventing memorization, even beyond the one-dimensional setting.

Optimal Transport-based Conformal Prediction

Conformal Prediction (CP) is a principled framework for quantifying uncertainty in blackbox learning models, by constructing prediction sets with finite-sample coverage guarantees. Traditional approaches rely on scalar nonconformity scores, which fail to fully exploit the geometric structure of multivariate outputs, such as in multi-output regression or multiclass classification. Recent methods addressing this limitation impose predefined convex shapes for the prediction sets, potentially misaligning with the intrinsic data geometry. We introduce a novel CP procedure handling multivariate score functions through the lens of optimal transport. Specifically, we leverage Monge-Kantorovich vector ranks and quantiles to construct prediction region with flexible, potentially non-convex shapes, better suited to the complex uncertainty patterns encountered in multivariate learning tasks. We prove that our approach ensures finite-sample, distribution-free coverage properties, similar to typical CP methods. We then adapt our method for multi-output regression and multiclass classification, and also propose simple adjustments to generate adaptive prediction regions with asymptotic conditional coverage guarantees. Finally, we evaluate our method on practical regression and classification problems, illustrating its advantages in terms of (conditional) coverage and efficiency.

Attention layers provably solve single-location regression

Attention-based models, such as Transformer, excel across various tasks but lack a comprehensive theoretical understanding, especially regarding token-wise sparsity and internal linear representations. To address this gap, we introduce the single-location regression task, where only one token in a sequence determines the output, and its position is a latent random variable, retrievable via a linear projection of the input. To solve this task, we propose a dedicated predictor, which turns out to be a simplified version of a non-linear self-attention layer. We study its theoretical properties, by showing its asymptotic Bayes optimality and analyzing its training dynamics. In particular, despite the non-convex nature of the problem, the predictor effectively learns the underlying structure. This work highlights the capacity of attention mechanisms to handle sparse token information and internal linear structures.

Physics-informed machine learning as a kernel method

Physics-informed machine learning combines the expressiveness of data-based approaches with the interpretability of physical models. In this context, we consider a general regression problem where the empirical risk is regularized by a partial differential equation that quantifies the physical inconsistency. We prove that for linear differential priors, the problem can be formulated as a kernel regression task. Taking advantage of kernel theory, we derive convergence rates for the minimizer of the regularized risk and show that it converges at least at the Sobolev minimax rate. However, faster rates can be achieved, depending on the physical error. This principle is illustrated with a one-dimensional example, supporting the claim that regularizing the empirical risk with physical information can be beneficial to the statistical performance of estimators.

An analysis of the noise schedule for score-based generative models

Score-based generative models (SGMs) aim at estimating a target data distribution by learning score functions using only noise-perturbed samples from the target. Recent literature has focused extensively on assessing the error between the target and estimated distributions, gauging the generative quality through the Kullback-Leibler (KL) divergence and Wasserstein distances. All existing results have been obtained so far for time-homogeneous speed of the noise schedule. Under mild assumptions on the data distribution, we establish an upper bound for the KL divergence between the target and the estimated distributions, explicitly depending on any time-dependent noise schedule. Assuming that the score is Lipschitz continuous, we provide an improved error bound in Wasserstein distance, taking advantage of favourable underlying contraction mechanisms. We also propose an algorithm to automatically tune the noise schedule using the proposed upper bound. We illustrate empirically the performance of the noise schedule optimization in comparison to standard choices in the literature.

Random features models: a way to study the success of naive imputation

Constant (naive) imputation is still widely used in practice as this is a first easy-to-use technique to deal with missing data. Yet, this simple method could be expected to induce a large bias for prediction purposes, as the imputed input may strongly differ from the true underlying data. However, recent works suggest that this bias is low in the context of high-dimensional linear predictors when data is supposed to be missing completely at random (MCAR). This paper completes the picture for linear predictors by confirming the intuition that the bias is negligible and that surprisingly naive imputation also remains relevant in very low dimension.To this aim, we consider a unique underlying random features model, which offers a rigorous framework for studying predictive performances, whilst the dimension of the observed features varies.Building on these theoretical results, we establish finite-sample bounds on stochastic gradient (SGD) predictors applied to zero-imputed data, a strategy particularly well suited for large-scale learning.If the MCAR assumption appears to be strong, we show that similar favorable behaviors occur for more complex missing data scenarios.

Sparse tree-based initialization for neural networks

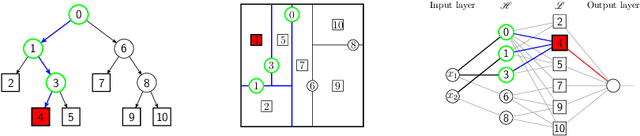
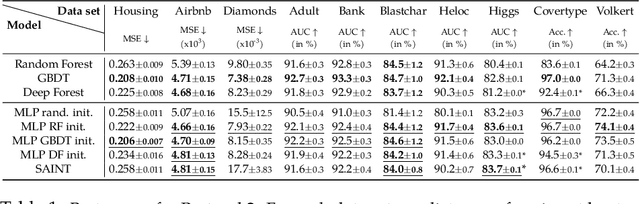
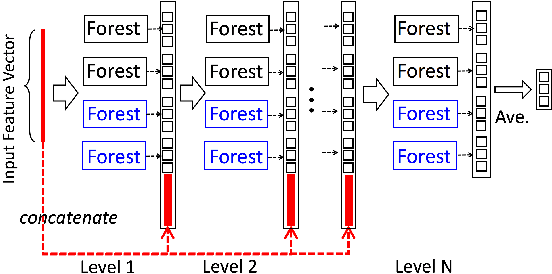
Dedicated neural network (NN) architectures have been designed to handle specific data types (such as CNN for images or RNN for text), which ranks them among state-of-the-art methods for dealing with these data. Unfortunately, no architecture has been found for dealing with tabular data yet, for which tree ensemble methods (tree boosting, random forests) usually show the best predictive performances. In this work, we propose a new sparse initialization technique for (potentially deep) multilayer perceptrons (MLP): we first train a tree-based procedure to detect feature interactions and use the resulting information to initialize the network, which is subsequently trained via standard stochastic gradient strategies. Numerical experiments on several tabular data sets show that this new, simple and easy-to-use method is a solid concurrent, both in terms of generalization capacity and computation time, to default MLP initialization and even to existing complex deep learning solutions. In fact, this wise MLP initialization raises the resulting NN methods to the level of a valid competitor to gradient boosting when dealing with tabular data. Besides, such initializations are able to preserve the sparsity of weights introduced in the first layers of the network through training. This fact suggests that this new initializer operates an implicit regularization during the NN training, and emphasizes that the first layers act as a sparse feature extractor (as for convolutional layers in CNN).

Minimax rate of consistency for linear models with missing values

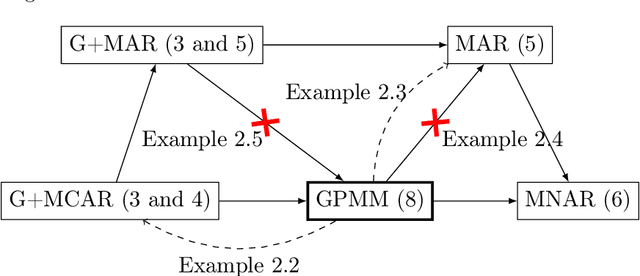
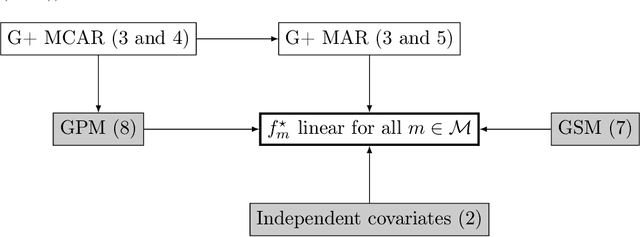
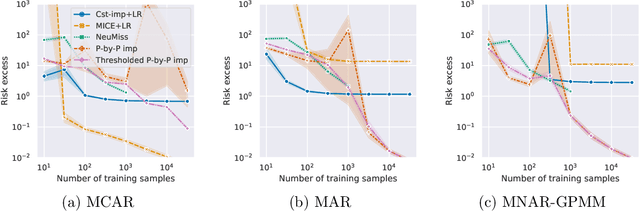
Missing values arise in most real-world data sets due to the aggregation of multiple sources and intrinsically missing information (sensor failure, unanswered questions in surveys...). In fact, the very nature of missing values usually prevents us from running standard learning algorithms. In this paper, we focus on the extensively-studied linear models, but in presence of missing values, which turns out to be quite a challenging task. Indeed, the Bayes rule can be decomposed as a sum of predictors corresponding to each missing pattern. This eventually requires to solve a number of learning tasks, exponential in the number of input features, which makes predictions impossible for current real-world datasets. First, we propose a rigorous setting to analyze a least-square type estimator and establish a bound on the excess risk which increases exponentially in the dimension. Consequently, we leverage the missing data distribution to propose a new algorithm, andderive associated adaptive risk bounds that turn out to be minimax optimal. Numerical experiments highlight the benefits of our method compared to state-of-the-art algorithms used for predictions with missing values.

Model-based Clustering with Missing Not At Random Data

In recent decades, technological advances have made it possible to collect large data sets. In this context, the model-based clustering is a very popular, flexible and interpretable methodology for data exploration in a well-defined statistical framework. One of the ironies of the increase of large datasets is that missing values are more frequent. However, traditional ways (as discarding observations with missing values or imputation methods) are not designed for the clustering purpose. In addition, they rarely apply to the general case, though frequent in practice, of Missing Not At Random (MNAR) values, i.e. when the missingness depends on the unobserved data values and possibly on the observed data values. The goal of this paper is to propose a novel approach by embedding MNAR data directly within model-based clustering algorithms. We introduce a selection model for the joint distribution of data and missing-data indicator. It corresponds to a mixture model for the data distribution and a general MNAR model for the missing-data mechanism, which may depend on the underlying classes (unknown) and/or the values of the missing variables themselves. A large set of meaningful MNAR sub-models is derived and the identifiability of the parameters is studied for each of the sub-models, which is usually a key issue for any MNAR proposals. The EM and Stochastic EM algorithms are considered for estimation. Finally, we perform empirical evaluations for the proposed submodels on synthetic data and we illustrate the relevance of our method on a medical register, the TraumaBase (R) dataset.