Solving Zero-Shot 3D Visual Grounding as Constraint Satisfaction Problems

3D visual grounding (3DVG) aims to locate objects in a 3D scene with natural language descriptions. Supervised methods have achieved decent accuracy, but have a closed vocabulary and limited language understanding ability. Zero-shot methods mostly utilize large language models (LLMs) to handle natural language descriptions, yet suffer from slow inference speed. To address these problems, in this work, we propose a zero-shot method that reformulates the 3DVG task as a Constraint Satisfaction Problem (CSP), where the variables and constraints represent objects and their spatial relations, respectively. This allows a global reasoning of all relevant objects, producing grounding results of both the target and anchor objects. Moreover, we demonstrate the flexibility of our framework by handling negation- and counting-based queries with only minor extra coding efforts. Our system, Constraint Satisfaction Visual Grounding (CSVG), has been extensively evaluated on the public datasets ScanRefer and Nr3D datasets using only open-source LLMs. Results show the effectiveness of CSVG and superior grounding accuracy over current state-of-the-art zero-shot 3DVG methods with improvements of $+7.0\%$ (Acc@0.5 score) and $+11.2\%$ on the ScanRefer and Nr3D datasets, respectively. The code of our system is publicly available at https://github.com/sunsleaf/CSVG.

GPTR: Gaussian Process Trajectory Representation for Continuous-Time Motion Estimation

Continuous-time trajectory representation has gained significant popularity in recent years, as it offers an elegant formulation that allows the fusion of a larger number of sensors and sensing modalities, overcoming limitations of traditional discrete-time frameworks. To bolster the adoption of the continuous-time paradigm, we propose a so-called Gaussian Process Trajectory Representation (GPTR) framework for continuous-time motion estimation (CTME) tasks. Our approach stands out by employing a third-order random jerk model, featuring closed-form expressions for both rotational and translational state derivatives. This model provides smooth, continuous trajectory representations that are crucial for precise estimation of complex motion. To support the wider robotics and computer vision communities, we have made the source code for GPTR available as a light-weight header-only library. This format was chosen for its ease of integration, allowing developers to incorporate GPTR into existing systems without needing extensive code modifications. Moreover, we also provide a set of optimization examples with LiDAR, camera, IMU, UWB factors, and closed-form analytical Jacobians under the proposed GP framework. Our experiments demonstrate the efficacy and efficiency of GP-based trajectory representation in various motion estimation tasks, and the examples can serve as the prototype to help researchers quickly develop future applications such as batch optimization, calibration, sensor fusion, trajectory planning, etc., with continuous-time trajectory representation. Our project is accessible at https://github.com/brytsknguyen/gptr .

Joint State and Parameter Estimation Using the Partial Errors-in-Variables Principle

This letter proposes a new method for joint state and parameter estimation in uncertain dynamical systems. We exploit the partial errors-in-variables (PEIV) principle and formulate a regression problem in the sense of weighted total least squares, where the uncertainty in the parameter prior is explicitly considered. Based thereon, the PEIV regression can be solved iteratively through the Kalman smoothing and the regularized least squares for estimating the state and the parameter, respectively. The simulations demonstrate improved accuracy of the proposed method compared to existing approaches, including the joint maximum a posterior-maximum likelihood, the expectation maximisation, and the augmented state extended Kalman smoother.

Gaussian Process on the Product of Directional Manifolds

We present a principled study on establishing Gaussian processes over variables on the product of directional manifolds. As a basic functional component, a manifold-adaptive kernel is presented based on the von Mises distribution for Gaussian process regression on unit circles. Afterward, a novel hypertoroidal von Mises kernel is introduced to enable topology-aware Gaussian processes on hypertori with consideration of correlational circular components. Based thereon, we enable multi-output regression for learning vector-valued functions on hypertori using intrinsic coregionalization model and provide analytical derivatives in hyperparameter optimization. The proposed multi-output hypertoroidal Gaussian process is further embedded to a data-driven recursive estimation scheme for learning unknown range sensing models of angle-of-arrival inputs. Evaluations on range-based localization show that the proposed scheme enables superior tracking accuracy over parametric modeling and common Gaussian processes.

Continuous-Time Ultra-Wideband-Inertial Fusion

We present a novel continuous-time online state estimation framework using ultra-wideband and inertial sensors. For representing motion states continuously over time, quaternion-based cubic B-splines are exploited with efficient solutions to kinematic interpolations and spatial differentiations. Based thereon, a sliding-window spline fitting scheme is established for asynchronous multi-sensor fusion and online calibration. We evaluate the proposed system, SFUISE (spline fusion-based ultra-wideband-inertial state estimation), in real-world scenarios based on public data set and experiments. The proposed spline fusion scheme is real-time capable and delivers superior performance over state-of-the-art discrete-time schemes. We release the source code and own experimental data set at https://github.com/KIT-ISAS/SFUISE.

Towards High-Performance Solid-State-LiDAR-Inertial Odometry and Mapping

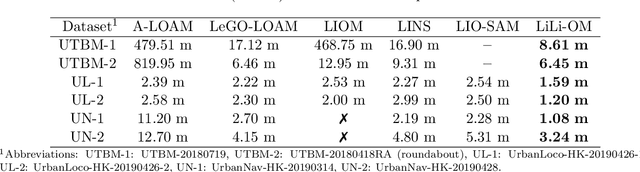
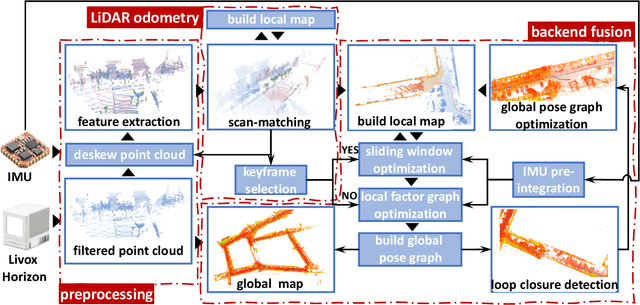
We present a novel tightly-coupled LiDAR-inertial odometry and mapping scheme for both solid-state and mechanical LiDARs. As frontend, a feature-based lightweight LiDAR odometry provides fast motion estimates for adaptive keyframe selection. As backend, a hierarchical keyframe-based sliding window optimization is performed through marginalization for directly fusing IMU and LiDAR measurements. For the Livox Horizon, a newly released solid-state LiDAR, a novel feature extraction method is proposed to handle its irregular scan pattern during preprocessing. LiLi-OM (Livox LiDAR-inertial odometry and mapping) is real-time capable and achieves superior accuracy over state-of-the-art systems for both LiDAR types on public data sets of mechanical LiDARs and in experiments using the Livox Horizon. Source code and recorded experimental data sets are available on Github.

Improved Pose Graph Optimization for Planar Motions Using Riemannian Geometry on the Manifold of Dual Quaternions

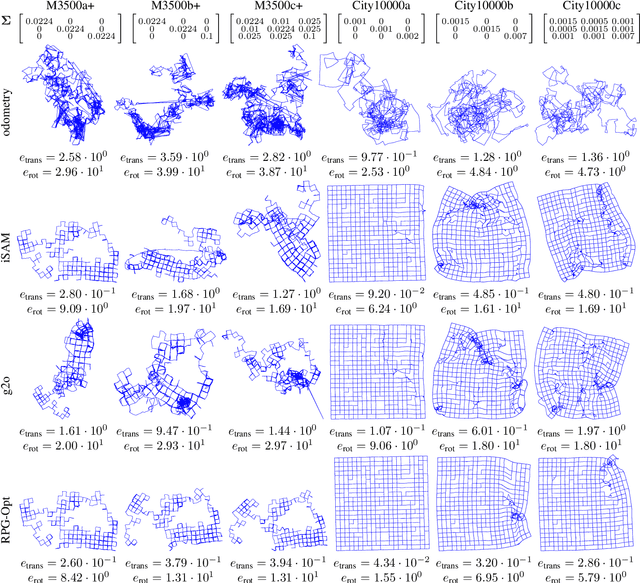
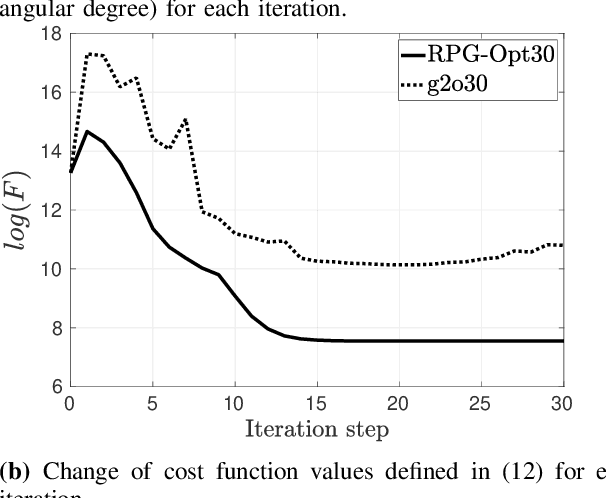
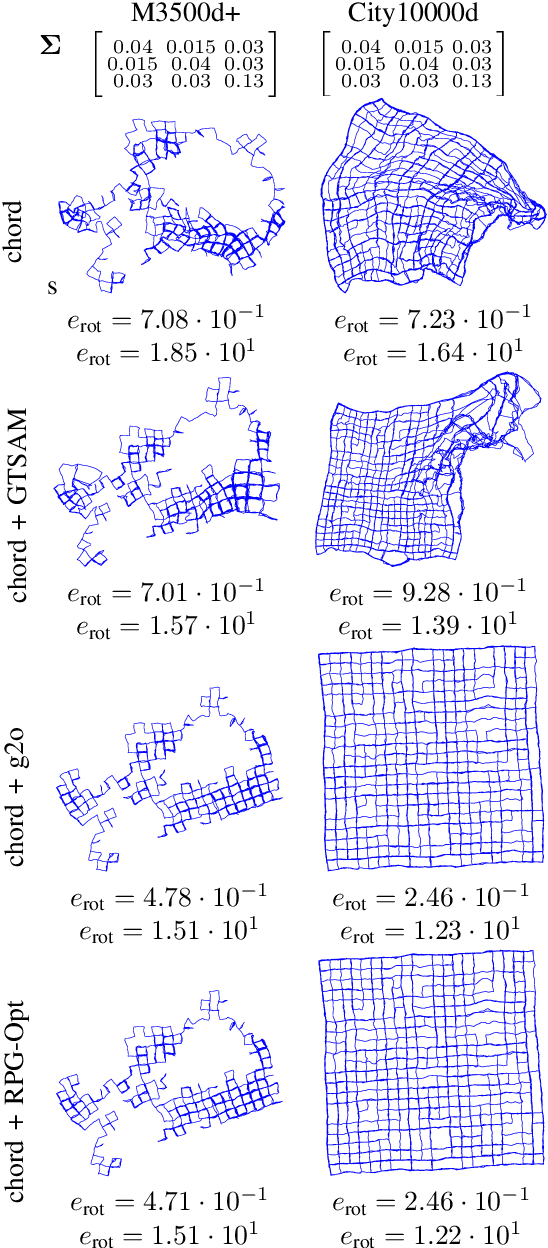
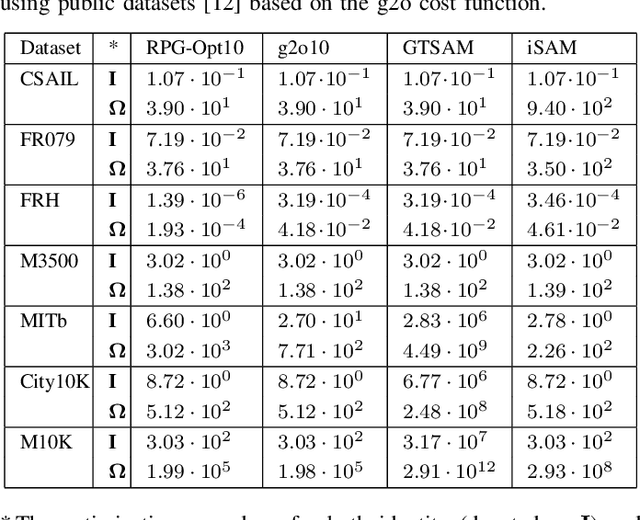
We present a novel Riemannian approach for planar pose graph optimization problems. By formulating the cost function based on the Riemannian metric on the manifold of dual quaternions representing planar motions, the nonlinear structure of the SE(2) group is inherently considered. To solve the on-manifold least squares problem, a Riemannian Gauss-Newton method using the exponential retraction is applied. The proposed Riemannian pose graph optimizer (RPG-Opt) is further compared with currently popular optimization frameworks using public planar pose graph datasets. Evaluations show that the proposed method gives equivalently accurate results as the state-of-the-art frameworks and shows better convergence robustness under large uncertainties of odometry measurements.